
前回の内容はこちらです.
(1),(2)は前回と同じで(3)以降が異なる問題です.
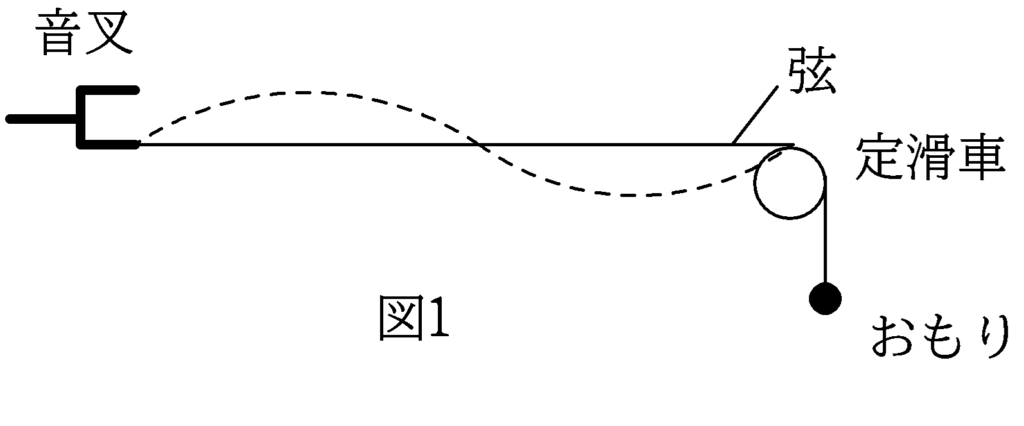
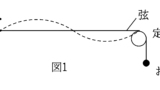
図1(この図の点線は腹が2個の場合を示している.)のように,おんさが弦につながれており,弦の他端は定滑車を通じておもりにつながれている.音叉の振幅は弦の振幅に比べて小さく,音叉と弦の接続部分,および弦と定滑車の接している部分は固定端反射をする.振動数$f_{0}$の音叉を用いて,弦の長さを$L$にしたところ,腹が1個の定常波ができた.このとき,次の問いに答えよ.
(1) 波長$\lambda_{1}$を求めよ.
(2) 弦を伝わる波の速さ$V_{1}$を求めよ.
音叉と弦の長さは変えずにおもりの重さを変えた.ただし,弦を伝わる速さ$V$は弦の張力$S$と線密度$\rho$を用いて
$V=\sqrt{\dfrac{S}{\rho}}$
と表される.
(3) 腹の数を2個にするためには,おもりの重さをもとの何倍にすればよいか.
(4) 腹の数を3個にするためには,おもりの重さをもとの何倍にすればよいか.
(5) $n$を自然数として,腹の数を$n$個にするためには,おもりの重さをもとの何倍にすればよいか.

共鳴,共振の問題では,
「定常波ができるとき」
の問題がほとんどです.
そこで,次のことに着目して解きましょう.
定常波の問題では次のことをあらかじめ知っておくとよい.
1. 固定端反射する場所は定常波の節になり,自由端反射する場合は定常波の腹となる.
2.波長を$\lambda$とする.定常波の隣り合う腹と節の距離は$\dfrac{1}{4}\lambda$
(1)

音叉と弦の接点と定滑車と弦の接点がともに固定端反射する場所なので,ここが定常波の節です.腹が1個の定常波ができるとのことなので,次のような図を考えることができますね.
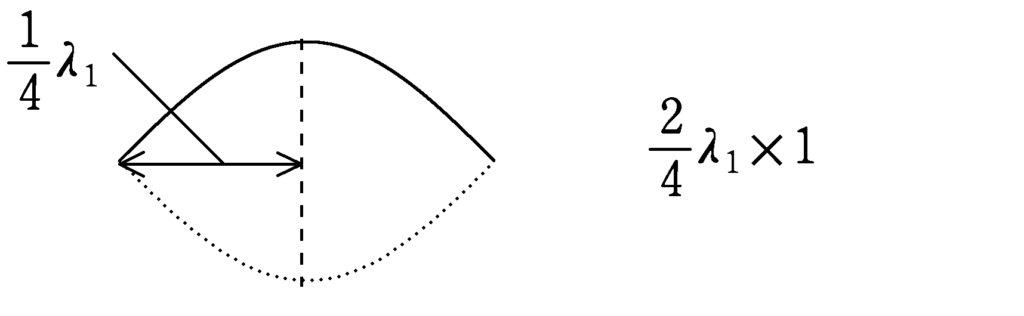
弦の長さが$L$なので
$L=\dfrac{2}{4}\lambda_{1}$
$\therefore \lambda_{1}=2L$ (答)
(2)
波が伝わる速さを$v$,媒質の振動の周期を$T$,振動数を$f$,波の波長を$\lambda$とすると,次の関係式が成り立つ.
$v=\dfrac{\lambda}{T}=f\lambda$
波の基本式に, $ \lambda_{1}=2L $を代入して
$\eqalign{V_{1}&=f_{0}\cdot \lambda_{1}&=2f_{0}L}$ (答)
(3)

腹の数と弦の長さが分かっているので波長の計算ができます.
波長を$\lambda_{2}$としましょう.
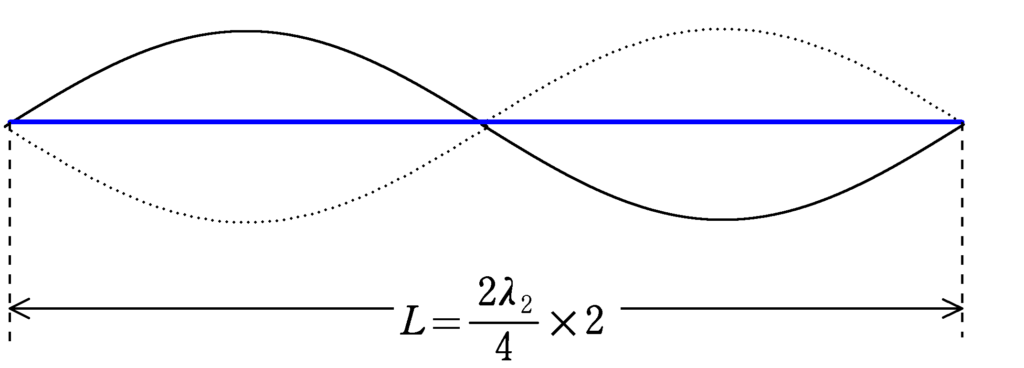

上図から
$L=\dfrac{2\lambda_{2}}{4}\times 2$
すなわち
$\lambda_{2}=L$
です.
$\lambda_{1}=2L$だったので,波長が$\dfrac{1}{2}$倍になっています.
波の基本式
$V=f\lambda$
の$f$(振動数)は変化せず(問題文に書かれています.)$\lambda$が$\dfrac{1}{2}$倍になるので,左辺の弦が伝わる速さも$\dfrac{1}{2}$倍になります.
問題文に書かれているように,張力の大きさ$S$と線密度$\rho$,波が弦を伝わる速さ$V$は
$V=\sqrt{\dfrac{S}{\rho}}$
です.今回は線密度$\rho$は変化しないので,$S$を変化させて$V$を$\dfrac{1}{2}$倍にします.
右辺に$\sqrt{}$がかかっていることに注意して張力$S$を$\dfrac{1}{4}$倍にすると,$V$が$\dfrac{1}{2}$倍になります.
だから,おもりのおもさを
$\dfrac{1}{4}$倍 (答)
にすればよいのです.
(4)
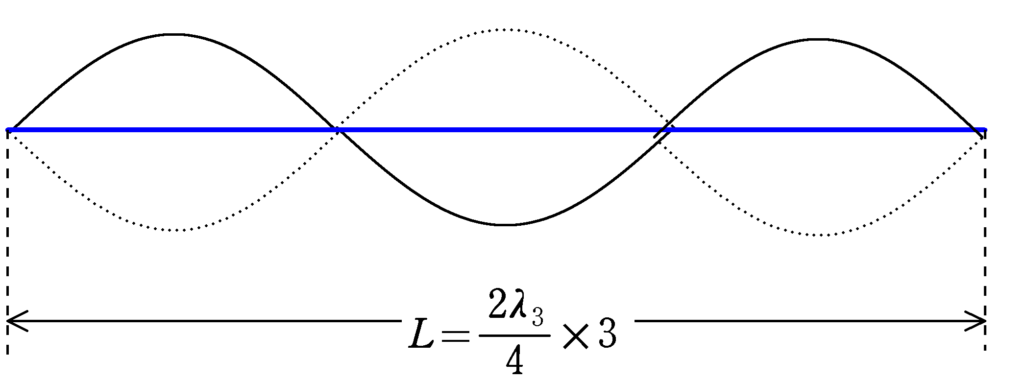

同じように計算していきます.
腹が3つだと,波長$\lambda_{3}$は
$L=\dfrac{2\lambda_{3}}{4}$
より
$\lambda_{3}=\dfrac{2L}{3}$
$\lambda_{1}=2L$なので,波長は$\dfrac{1}{3}$倍です.
波の基本式
$V=f\lambda$
について,振動数が変化しないので,右辺が波長が$\dfrac{1}{3}$倍だと,左辺の波の速さも$\dfrac{1}{3}$倍です.
さらに,
$V=\sqrt{\dfrac{S}{\rho}}$
線密度が変化しないので,左辺の波の速さが$\dfrac{1}{3}$倍だと,右辺の張力が$\dfrac{1}{9}$倍となります.(※まるで腹の数が変化した結果おもりが$1/9$倍になるような書き方ですが,実際は反対で,おもりを$1/9$倍にすると,腹の数が3つになります.)
したがって,おもりの重さは
$\dfrac{1}{9}$倍 (答)
(5)
腹が$n$個→ 波長が$\dfrac{1}{n}$倍
$V=f\lambda$と振動数が変化しないことから
波長が$\dfrac{1}{n}$倍→波の伝わる速さも$\dfrac{1}{n}$倍
$V=\sqrt{\dfrac{S}{\rho}}$ と線密度が変化しないことから
速さが$\dfrac{1}{n}$倍→張力が$\dfrac{1}{n^{2}}$倍
したがって,おもりを$\dfrac{1}{n^{2}}$倍(答)にすると腹が$n$個できる.



コメント