
放射性崩壊の問題で出てくる半減期の式は次のようになります.
今回は,この「半減期の式」を導出していきます.
微分を使わないものは入試問題で出題されています.
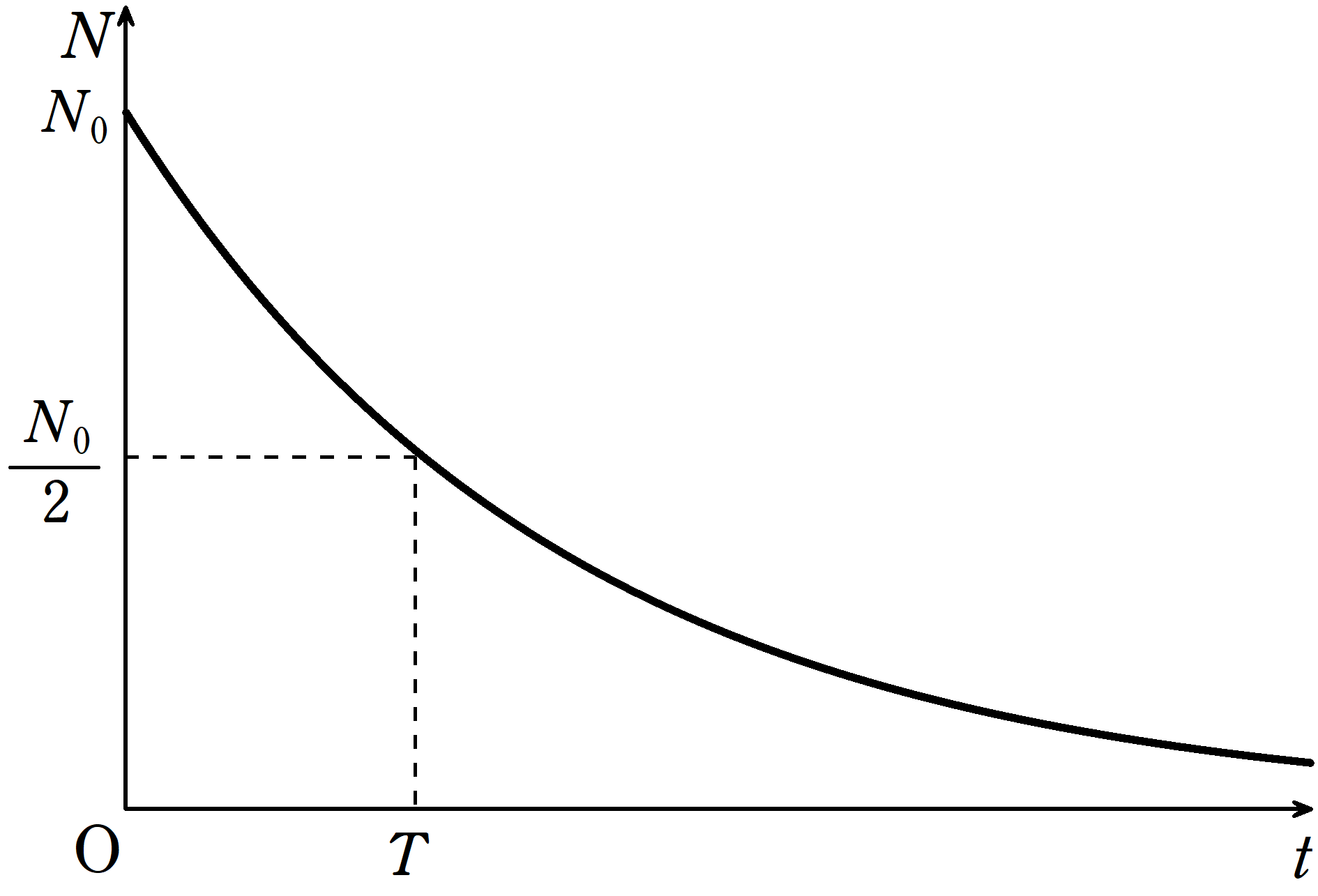
時刻$t=0$における放射性元素の数を$N_{0}$とする.時刻$t$における放射性元素の数を$N(t)$とする.半減期(放射性元素の数が半分になるまでの時間)を$T$とすると,次の式が成り立つ.
$N(t)=N_{0}\left(\dfrac{1}{2}\right)^{\frac{t}{T}}$
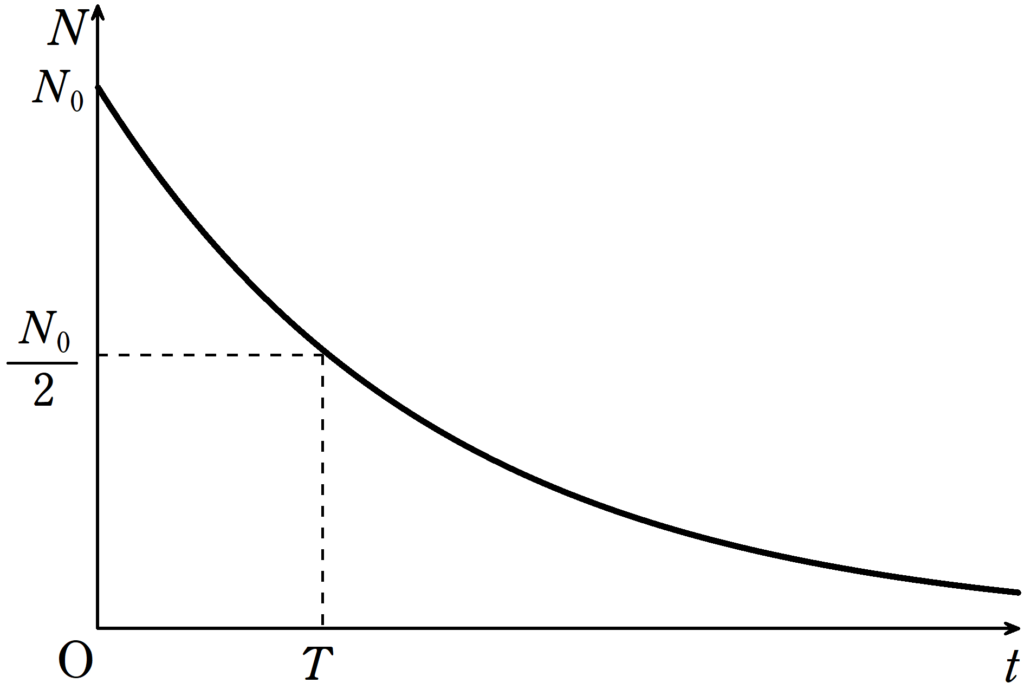

単位時間あたりに崩壊する数$\left(\dfrac{dN(t)}{dt}\right)$は,そのときの放射性元素の数$N(t)$に比例します.
定数$\lambda$を用いて次のように表すことができます.
$\dfrac{dN(t)}{dt}=-\lambda N(t)$ $\dots (\ast)$

$\lambda$を崩壊定数といいます.
右辺に「$-$」があるのは,崩壊すると放射性元素の数が減っていくからです.
$(\ast)$の微分方程式を解きます.
$(\ast)$について,両辺$N(t)$で割ると,
$\dfrac{1}{N(t)}\dfrac{dN(t)}{dt}=-\lambda$
両辺$t$で積分します.積分定数を$C$としましょう.
$\displaystyle{\eqalign{\int \dfrac{1}{N(t)}\dfrac{dN(t)}{dt} dt&=-\int \lambda dt\cr \int \dfrac{1}{N(t)}dN(t)&=-\lambda t+C \cr \log N(t)&=-\lambda t+C\\&=\log e^{-\lambda t+C}}}$
$\therefore$ $\eqalign{N(t)&=e^{-\lambda t+C}\\&=e^{C}e^{-\lambda t}}$

$e^{C}$は定数なので,$K$とおきます.
$N(t)=Ke^{-\lambda t}$ $\dots (2\ast)$

初期条件,$t=0$のとき,$N(0)=N_{0}$を代入しましょう.
$N_{0}=Ke^{0}$
$\therefore K=N_{0}$
これを$(2\ast)$に代入して
$N(t)=N_{0}e^{-\lambda t}$ $\dots (3\ast)$

時刻$t=T$のとき,数が$\dfrac{N_{0}}{2}$であることを$(3\ast)$に代入してみます.
$\dfrac{N_{0}}{2}=N_{0}e^{-\lambda T}$
$e^{-\lambda T}=\dfrac{1}{2}$ $\dots (4\ast)$
両辺底が$e$の対数を取って,$T$を求めると,
$-\lambda T=\log\left(\dfrac{1}{2}\right)$
$T=\dfrac{\log 2}{\lambda}$

$\log 2\fallingdotseq 0.693$なので,
$T\fallingdotseq \dfrac{0.693}{\lambda}$です.
$(4\ast)$の$e^{-\lambda T}=\dfrac{1}{2}$をつくって,$(3\ast)$の$N(t)=N_{0}e^{-\lambda t}$を変形します.
$\eqalign{N(t)&=N_{0}\left(e^{-\lambda T}\right)^{\frac{t}{T}}\\&=N_{0}\left(\dfrac{1}{2}\right)^{\frac{t}{T}}}$

以上で,半減期の式が導出できました.


コメント