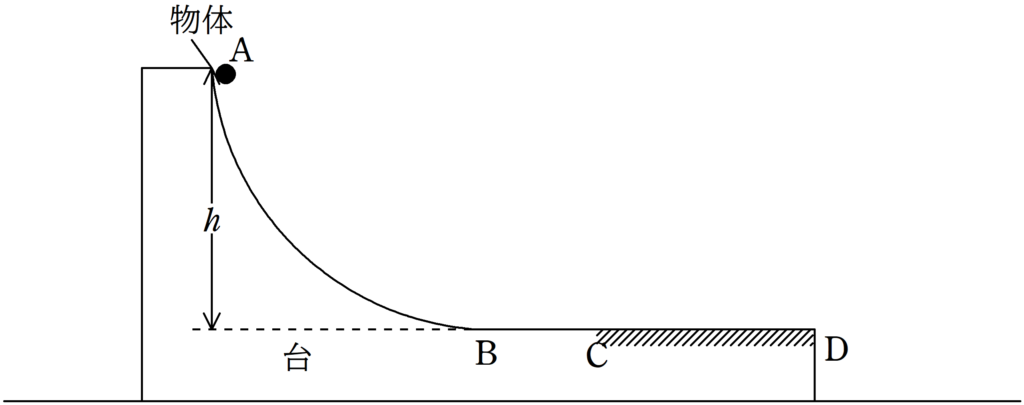
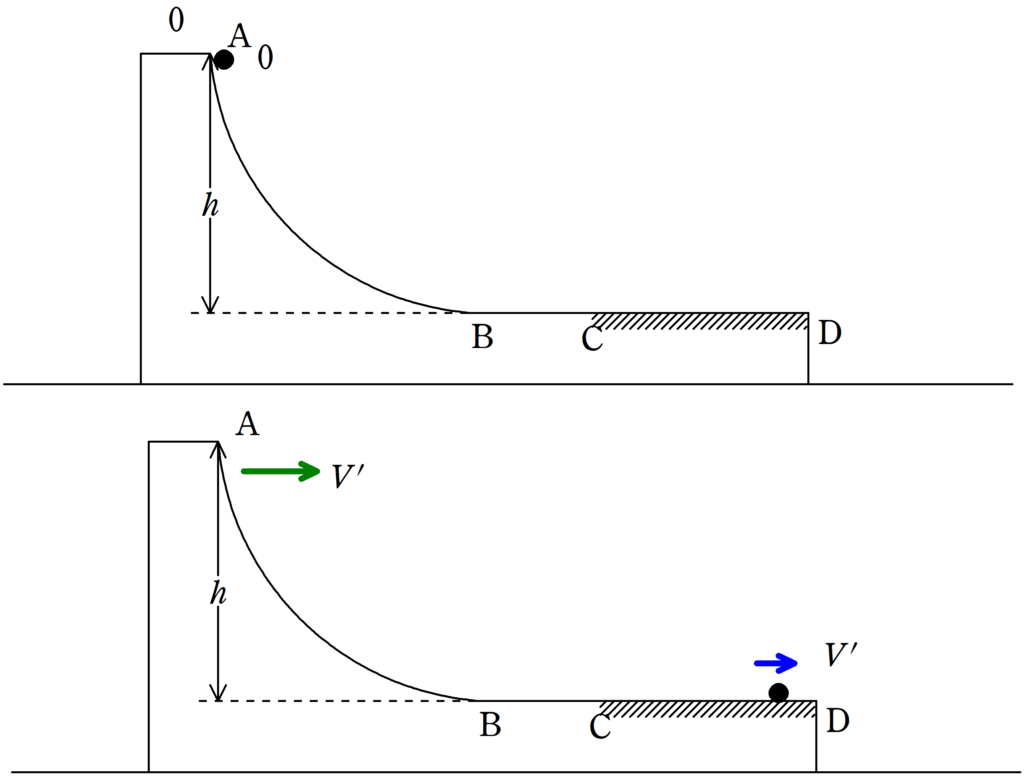
図のように水平でなめらかな床の上に質量$M$の台があり,台は曲面$\rm AB$部分と,水平部分$\rm BCD$からなっている.曲面$\rm AB$および,水平部分$\rm BC$はなめらかであり,$\rm CD$は粗い面になっている.水平部分から高さ$h$の曲面の位置に質量$m$の物体をおき,台とともに静止させた状態から静かに手を放したところ,物体と台は運動をはじめた.ただし,速度の向きは上図の右向きである.
重力加速度の大きさを$g$として,次の問いに答えよ.
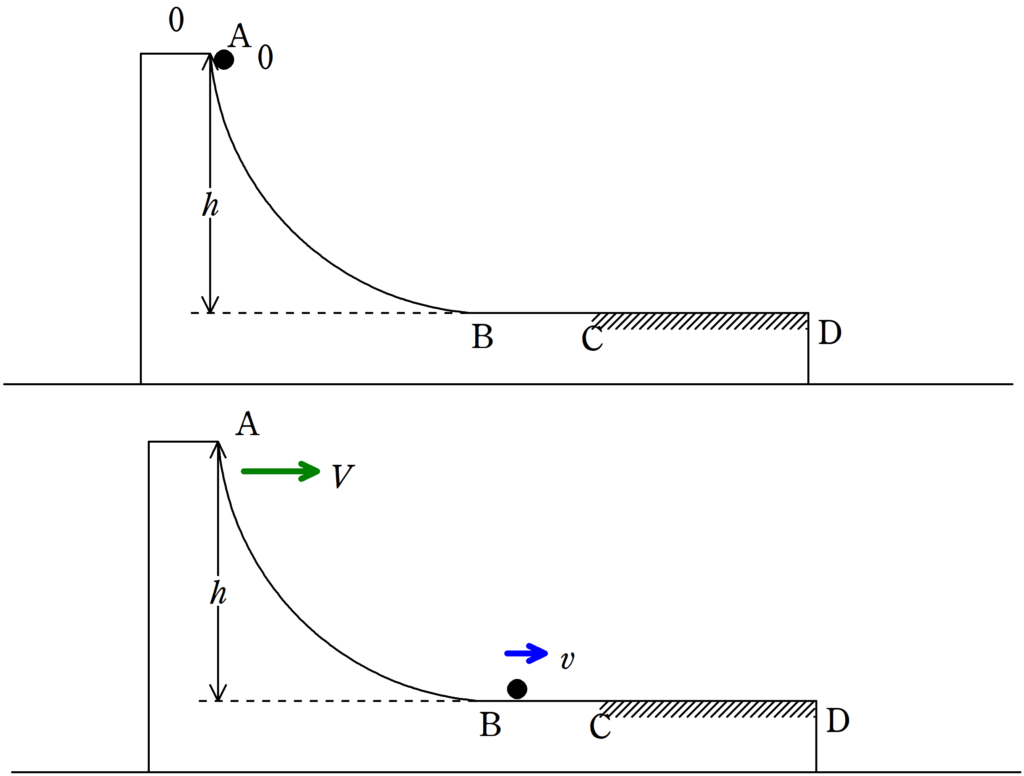
(1) 物体が$\rm B$にたどり着いた後,物体が$\rm BC$部分を運動しているときの静止した床から見た物体の速度を$v$,台の速度を$V$とする.$v$と$V$を$m$,$M$,$g$,$h$を用いて表せ.
(2) (1)の後,物体は$\rm CD$部分に到達し,やがて台に対して静止した.このとき,台と物体の速度$V^{\prime}$を求めよ.
(3) (2)において,物体は$\rm C$から距離$l$だけ滑って台に対して静止していた.このことから,物体と台の動摩擦係数$\mu$を$M$,$m$,$g$,$h$,$l$から必要なものを用いて表せ.
<解答>
(1)
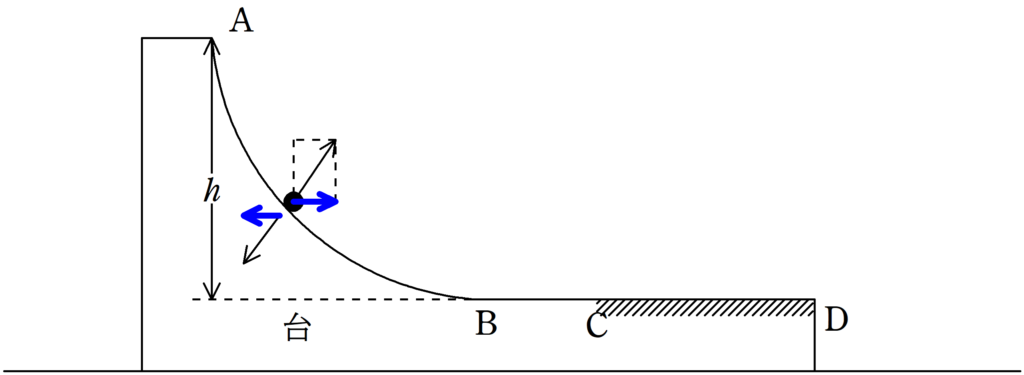

上図のように,物体と台にはたらく水平方向の力の和は0なので,台と物体を対象とした水平方向の運動量が保存します.
質量$m_{1}$の物体1と質量$m_{2}$の物体2の速度を$v_{1}$,$v_{2}$とする.
物体1と物体2の力積の和が0のとき,次の式が成り立つ.
$m_{1}v_{1}+m_{2}v_{2}=$一定
これを運動量保存則という.
運動量保存則は次のようなときに立てることが多い.
.2つ以上の物体の運動
・水平方向の成分の力の和が0のとき
・鉛直方向であっても,空中衝突や空中分裂などの,非常に短い時間で外力がはたらく場合は,近似的に運動量保存則を立てる.

また,台と物体を対象とした力学的エネルギーも保存します.
力学的エネルギーが保存する理由はこちらを参考にしてみてください.
★ 運動量保存則
$0=mv+MV$ $\dots (\ast)$
★ 力学的エネルギー保存則
$mgh=\dfrac{1}{2}mv^{2}+\dfrac{1}{2}MV^{2}$ $\dots (2\ast)$
$(\ast)$より,$v=-\dfrac{M}{m}V$と変形して$(2\ast)$に代入すると
$\eqalign{mgh&=\dfrac{1}{2}m\dfrac{M^{2}}{m^{2}}V^{2}+\dfrac{1}{2}MV^{2}\cr \dfrac{1}{2}MV^{2}(\dfrac{M}{m}+1)&=mgh \cr \dfrac{1}{2}MV^{2}\cdot \dfrac{M+m}{m}&=mgh\cr V^{2}&=\dfrac{2m^{2}gh}{M(M+m)}}$
$V<0$より
$\therefore V=-m\sqrt{\dfrac{2gh}{M(M+m)}}$(答)
さらに,$v=-\dfrac{M}{m}V$より
$v=M\sqrt{\dfrac{2gh}{M(M+m)}}$ (答)
(2)
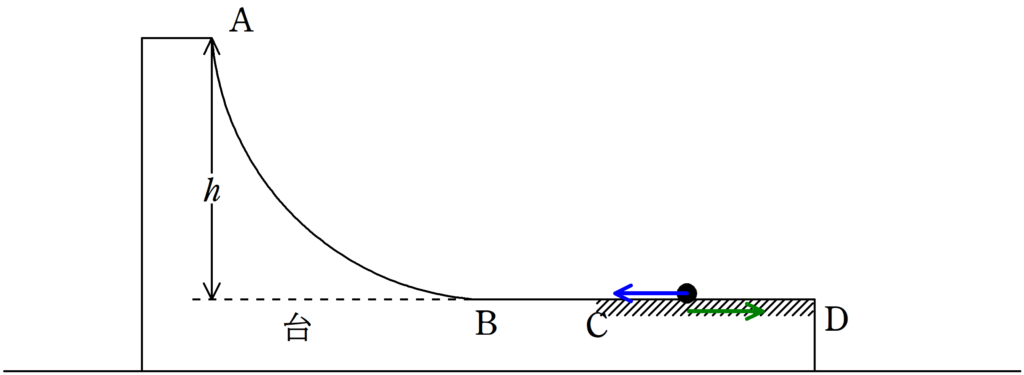

物体が$\rm CD$部分にあるときも水平方向には摩擦力の作用反作用だけしかはたらかないので,運動量が保存します.
すなわち,水平方向の運動量ははじめからずっと保存しているのです.
★ 運動量保存則
$0=(M+m)V^{\prime}$ $\therefore V^{\prime}=0$ (答)
(3)

最後に
力学的エネルギー変化=非保存力がした仕事
の式を立てましょう.
はじめ,静止していた状態からスタートして,(2)より,最終的には静止するので運動エネルギー変化0です.失う力学的エネルギーは重力による位置ネルギーですね.
★ 力学的エネルギー変化=非保存力がした仕事
$0-mgh=-\mu mgl$ $\therefore \mu =\dfrac{h}{l}$ (答)
※ 2つの物体が動いているのに,片方の仕事しか考えていないのでは??と思った方は下の問題の解説をよく読んでおいてください.





コメント