
今回は,電流計と電圧計の値を測定することで求めた抵抗値の相対誤差の問題です.
相対誤差は,入試問題では説明してくれることが多いです.
★ 誤差
誤差$=$測定値$-$真の値
★ 相対誤差
相対誤差$=\dfrac{\rm 誤差の絶対値}{\rm 真の値}$

それでは,さっそく問題を解いてみましょう.
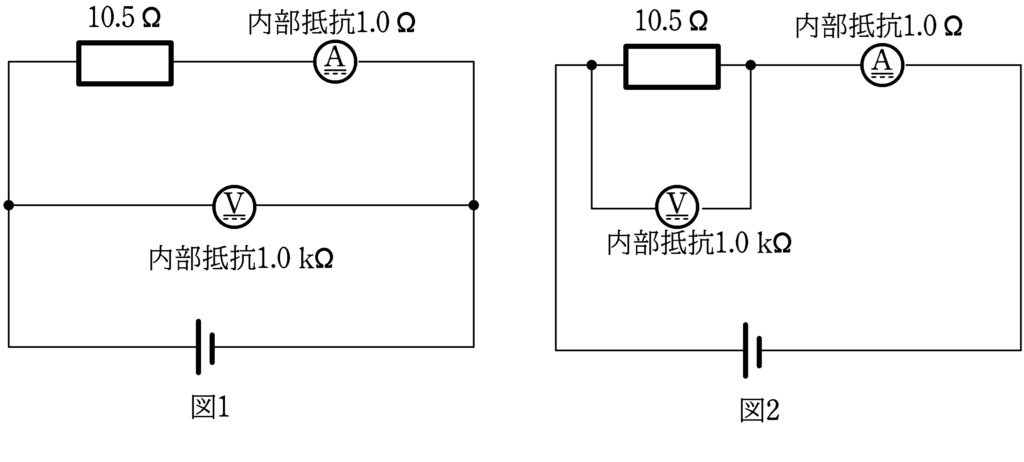
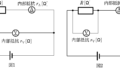
内部抵抗の無視できる直流電源と抵抗値$10.5 \rm \Omega$の抵抗R,内部抵抗が$1.0 \rm \Omega$の電流計と内部抵抗が$1.0 \rm k\Omega$の電圧計を図1,図2のように接続した回路がある.
電圧計で測定された値を電流計で測定された値で割った値を,抵抗の測定値とする.真の値($\rm 10.5\Omega$)から測定値の差を取った値を誤差という.
$\dfrac{|\rm 誤差|}{\rm 真の値}$
の値が小さいのは,図1,図2のどちらか.

どっちでも同じようなものじゃないんだ・・・

実は,図1では,抵抗Rを流れる電流を正しく測定していますが,抵抗Rにかる電圧は正しく測定されていません.(電流計の内部抵抗で落ちる電圧を含めて測定してしまっているため)
また,図2では,抵抗Rにかかる電圧は正しく測定されていますが,抵抗Rを流れる電流は正しく測定されていません.(電圧計を流れる電流も測定されているため)
下図では,図1の電流計で測定された電流の値を$I_{1} [\rm A] $,電圧計で測定された電圧の値を$V_{1} [\rm V] $,また,図2の電流計で測定された電流の値を$I_{2} [\rm A] $,電圧計で測定された電圧の値を$V_{2} [\rm V] $としています.
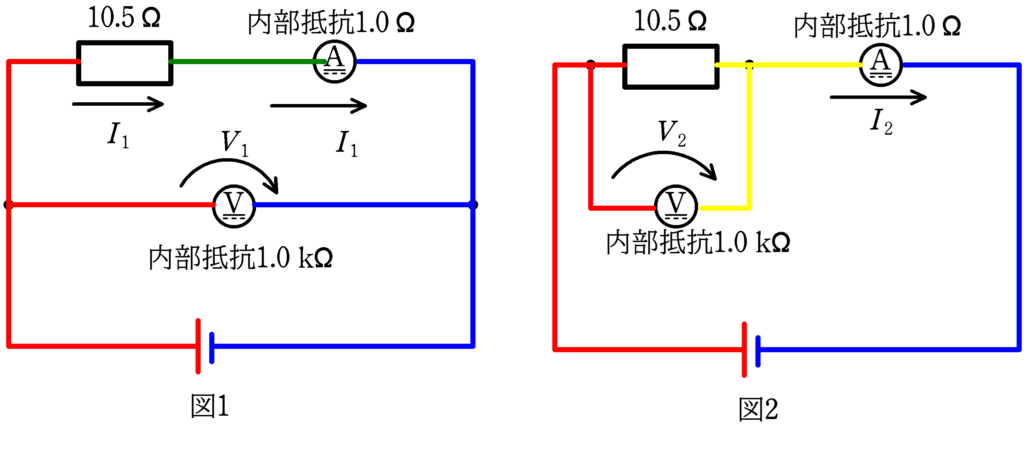

たしかに,図1では抵抗Rにかかる電圧(赤と緑の電位の差)と電圧計にかかるで電圧(赤と青の電位の差)が異なるね.一方,一直線上にあるから,電流計に流れる電流と抵抗Rに流れる電流は一緒だ!
さらに,図2では,電圧計にかかる電圧と抵抗Rにかかる電圧(どちらも赤と黄色の電位の差)はどちらも同じだね.一方,電流計に流れる電流と抵抗Rに流れる電流は異なるね.

それでは,図1,図2の測定値をそれぞれ
$R_{\rm 測定値1}$,$R_{\rm 測定値2}$
としましょう.
すると,
$R_{\rm 測定値1}=\dfrac{V_{1}}{I_{1}}$
$R_{\rm 測定値2}=\dfrac{V_{2}}{I_{2}}$
となります.
そして,$V_{1}$を$I_{1}$で,$I_{2}$を$V_{2}$で表してみたいと思います.(とりあえず1つの文字にしてもらえればよいです.)
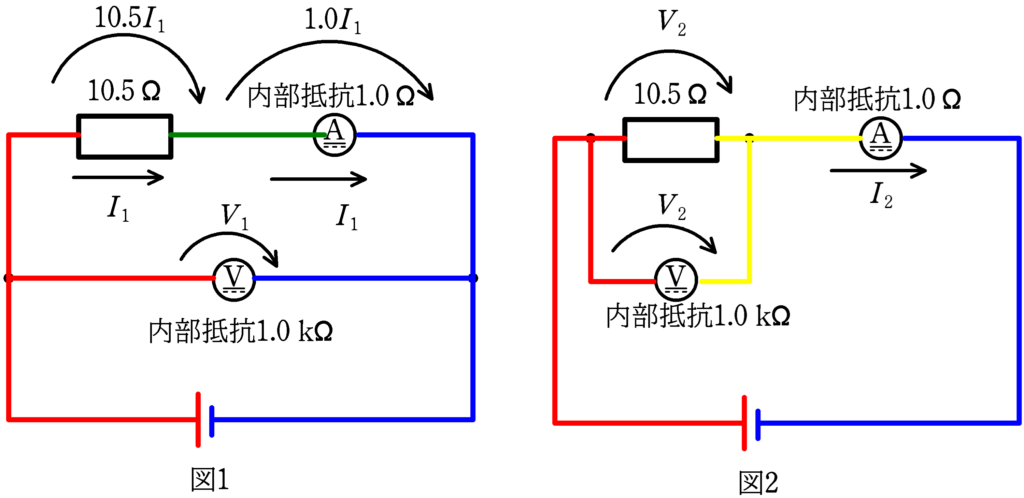
★ 図1について
抵抗Rにかかる電圧は,オームの法則より
$10.5I_{1} [\rm V]$ $\cdots (\ast)$
電流計にかかる電圧は,オームの法則より
$1.0I_{1} [\rm V] $ $\cdots (2\ast)$
$(\ast)+(2\ast)$が$V_{1}$に等しいから
$V_{1}=10.5I_{1}+1.0I_{1} [\rm V]$
したがって,測定値は
$\eqalign{R_{\rm 測定値1}&=\dfrac{V_{1}}{I_{1}}\\&=\dfrac{10.5I_{1}+1.0I_{1}}{I_{1}}\\&=11.5 [\Omega]}$
★ 図2について
電圧計に流れる電流は,オームの法則より
$\dfrac{V_{2}}{1.0\times 10^{3}} [\rm A] $ $\cdots (3\ast)$
抵抗Rに流れる電流は,オームの法則より
$\dfrac{V_{2}}{10.5} [\rm A] $ $\cdots (4\ast)$
$(3\ast)+(4\ast)$が$I_{2}$に等しいので
$\eqalign{I_{2}&=\dfrac{V_{2}}{1.0\times 10^{3}}+\dfrac{V_{2}}{10.5}\\&=\dfrac{2021}{21000}V_{2} [\rm A]}$
したがって,測定値は
$\eqalign{R_{\rm 測定値2}&=\dfrac{V_{2}}{I_{2}}\\&=\dfrac{V_{2}}{\dfrac{2021}{21000}V_{2}}\\&=\dfrac{21000}{2021}\fallingdotseq 10.39 [\Omega]}$

それぞれの誤差の絶対値は
$|10.5-R_{\rm 測定値1}|=1.0 [\Omega] $
$|10.5-R_{\rm 測定値2}|\fallingdotseq 0.11 [\Omega] $
だから,図2(答)の方が誤差が小さいんだね.
真の値はどちらも同じだから,相対誤差もやはり図2の方が小さいね.


コメント
[…] […]
[…] […]