[演習]運動量変化と力積3

PHYさん

前回の内容はこちらです．

[演習問題]運動量変化と力積2

運動量変化と力積ダウンロード 問題 図1のように，正三角形$\rm ABC$の辺に沿って，質量$m$の質点が速さ$v$で$\rm A\rightarrow \rm B\rightarrow \rm C$の向きにまわっている．このとき，次の問...

physicmath.net

2021.03.09

問題

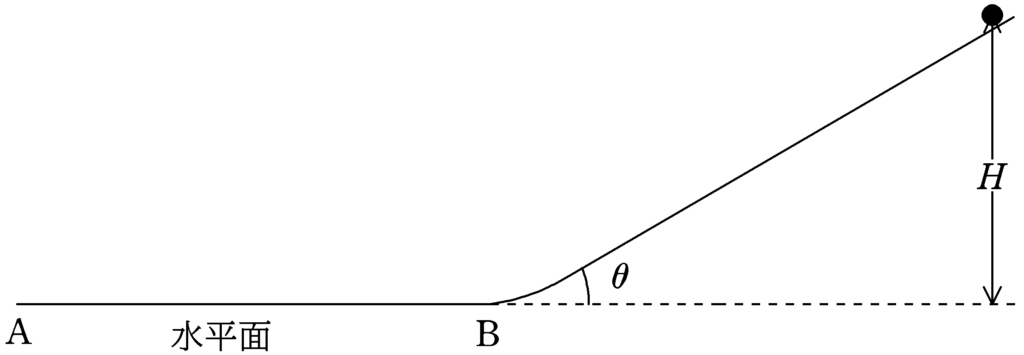
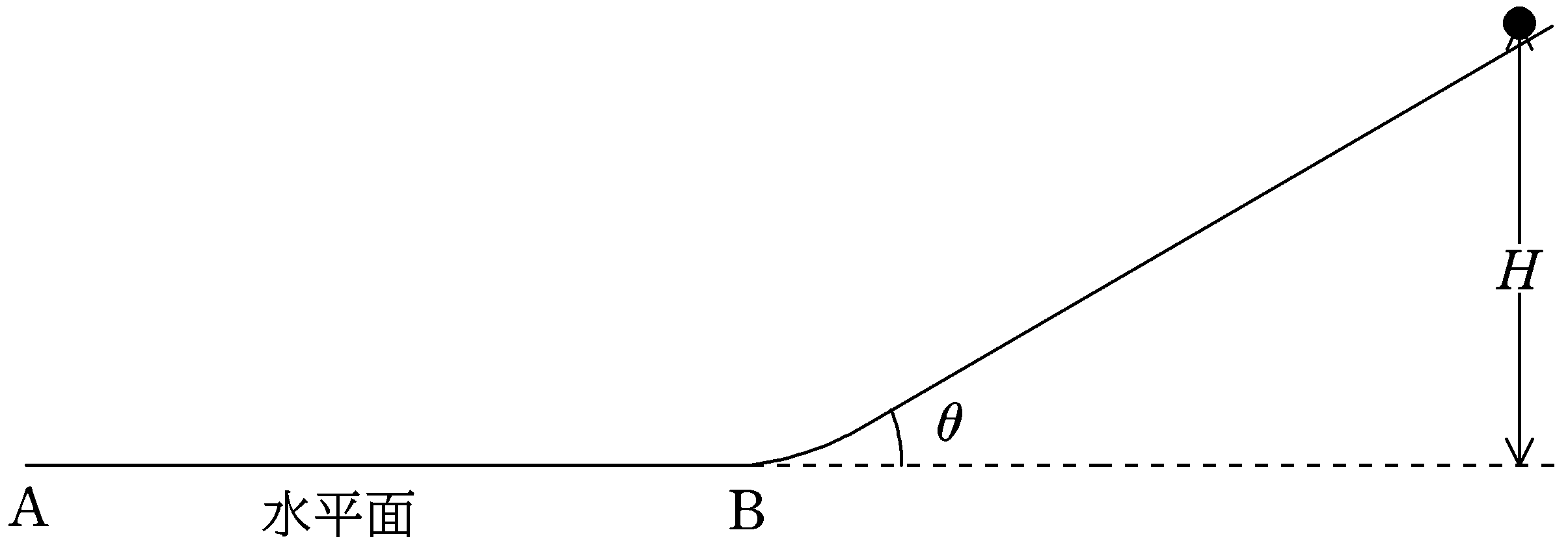
図のように，水平面ABとなめらかにつながっている傾角$\theta$の斜面がある．斜面上の水平面からの高さ$H$の位置に質量$m$の小球を静かにおいてはなしたことろ小球は斜面上を運動し，水平面に到達した．

斜面から水平面にうつりかわる際に小球が受ける力積の大きさを求めよ．ただし，斜面から水平面にうつる際に速さは変化せず．小球は斜面および水平面から常に離れずに運動したものとする．

＜解答＞

NEKO

力積は直接求めることは困難なので，運動量変化を考えましょう．

★　力学的エネルギー保存則

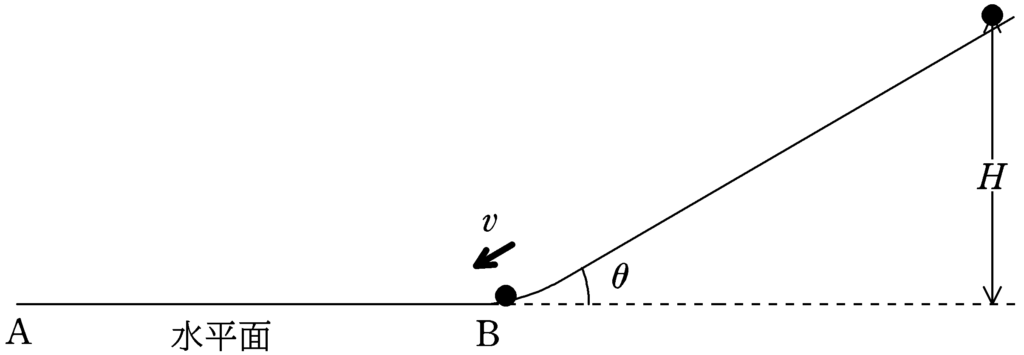
斜面から水平面に達するときの速さを$v$として，力学的エネルギー保存則より

$\dfrac{1}{2}mv^{2}=mgH$

$\therefore v=\sqrt{2gH}$

NEKO

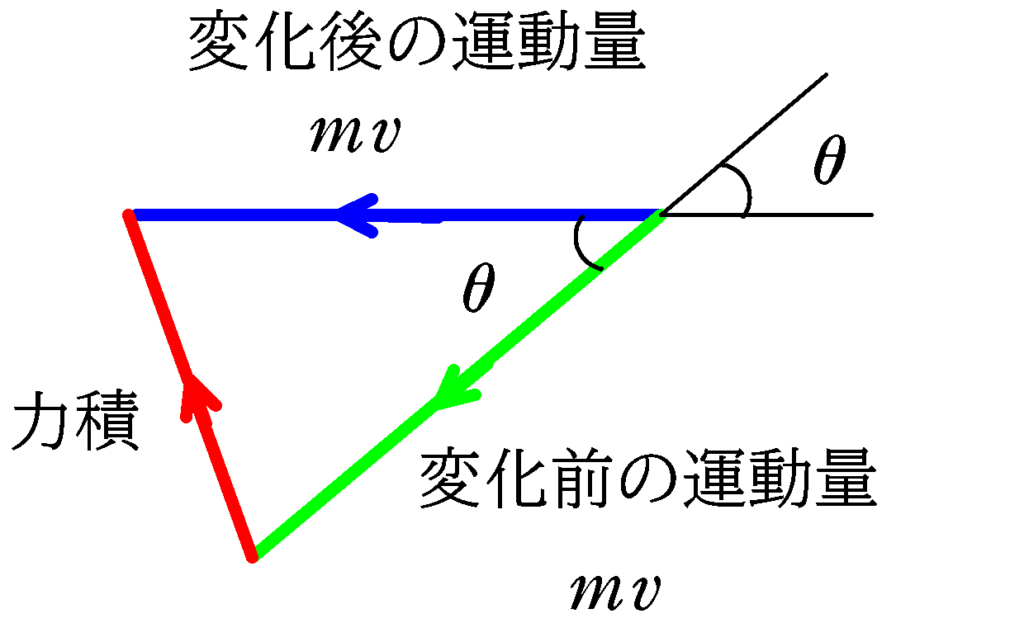
運動量変化と力積は次の図を確認しましょう．

NEKO

つまり力積の大きさは上図の赤色の部分の長さだね．

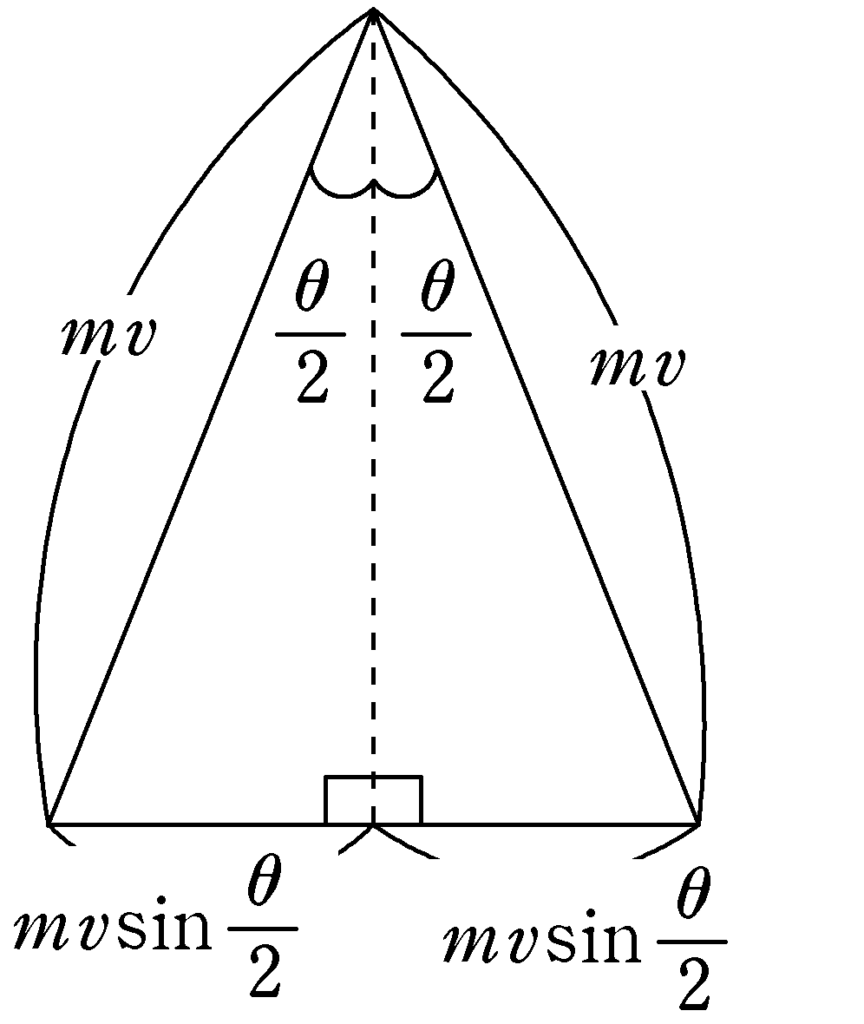
上図より，力積の大きさは，$v=\sqrt{2gH}$を考慮して

$2mv\sin\dfrac{\theta}{2}=2m\sqrt{2gH}\sin\dfrac{\theta}{2}$　(答)