
$y=\sin\theta \cdots (\ast)$と$y=\sin(\theta+\delta) \cdots (2\ast)$のグラフがあるとしましょう.
$(\ast)$と$(2\ast)$の交点の$\theta$座標は$(\ast)$のグラフを$\theta$軸方向に$\alpha$,$(2\ast)$のグラフを$\theta$軸方向に$-\alpha$平行移動しても変化しません.
(ただし,$\delta\neq2\pi\times 整数$,つまり$(\ast)$のグラフと$(2\ast)$のグラフが重なっていない状態とします)
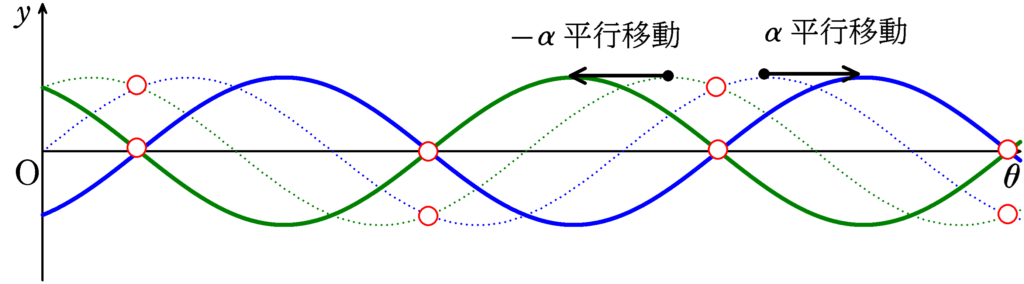
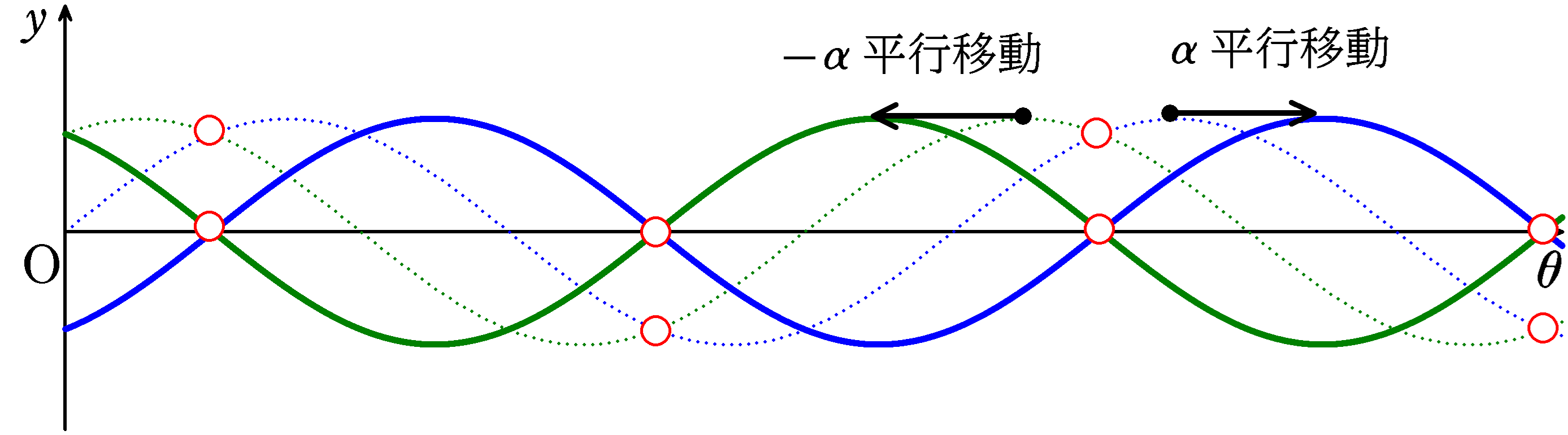
青点線が$y=\sin\theta$,緑点線が$y=\sin(\theta+\delta)$,青太線が$y=\sin\left(\theta-\alpha\right)$,緑太線が$y=\sin\left(\theta+\delta+\alpha\right)$

上のグラフをみると,交点の$\theta$座標は変化していなさそうだね.

この事実は,定常波の問題でも使います。
計算してみましょう.
$y=\sin\theta$と$y=\sin(\theta+\delta)$の交点の$\theta$座標について
$\sin\theta=\sin(\theta+\delta)$について解く.ただし,$n$を整数として,$\delta\neq 2\pi n$とする.(重ならないという条件)
$\sin(\theta+\delta)-\sin\theta=0$ $(\sharp)$
左辺を「差」→「積」の変換式で変形すると
まず,正弦の加法定理を書き出します.
$\sin(A+B)=\sin A\cos B+\cos A\sin B$ $\cdots (3\ast)$
$\sin(A-B)=\sin A\cos B-\cos A\sin B$ $\cdots (4\ast)$
$(3\ast)-(4\ast)$を計算します.
$\sin(A+B)-\sin(A-B)=2\cos A\sin B$ $\cdots (\clubsuit)$
$(\clubsuit)$の左辺と$(\sharp)$の左辺との対応関係を書き出しましょう.
$A+B= \theta+\delta $ $\cdots (5\ast)$
$A-B= \theta $ $\cdots (6\ast)$
$(5\ast)+(6\ast)$を計算し,$A$を求めます.
$2A=2\theta+\delta$
$\therefore A=\theta+\dfrac{\delta}{2}$ $\cdots (7\ast)$
$(5\ast)-(6\ast)$を計算し,$B$を求めます.
$2B=\delta$
$\therefore B=\dfrac{\delta}{2}$ $\cdots (8\ast)$
$(7\ast)$,$(8\ast)$を$(\clubsuit)$の右辺に代入して積の形をつくります.
$\sin(\theta+\delta)-\sin\theta=2\cos\left(\theta+\dfrac{\delta}{2}\right)\sin\dfrac{\delta}{2}$
よって,$(\sharp)$の式は
$2\cos\left(\theta+\dfrac{\delta}{2}\right)\sin\dfrac{\delta}{2}=0$
$\therefore\,\,\, \cos\left(\theta+\dfrac{\delta}{2}\right)=0 または \sin\dfrac{\delta}{2}=0$
しかし,$\delta\neq 2\pi n$より,$\dfrac{\delta}{2}\neq \pi n$なので,$\sin\dfrac{\delta}{2}\neq 0$となる.よって,$y=\sin\theta$と$y=\sin(\theta+\delta)$の交点の$\theta$座標を$\theta_{0}$とすると,$\theta_{0}$は次の式を満たす.
$\cos\left(\theta_{0}+\dfrac{\delta}{2}\right)=0$ $\cdots (9\ast)$
$y=\sin\left(\theta-\alpha\right)$と$y=\sin\left(\theta+\delta+\alpha\right)$の交点の$\theta$座標について
$\sin\left(\theta-\alpha\right)=\sin\left(\theta+\delta+\alpha\right)$より
$\sin\left(\theta+\delta+\alpha\right)-\sin\left(\theta-\alpha\right)=0 \cdots (2\sharp)$
同様に左辺を「差」→「積」にします.
まず,正弦の加法定理を書き出します.
$\sin(A+B)=\sin A\cos B+\cos A\sin B$ $\cdots (3\ast)$
$\sin(A-B)=\sin A\cos B-\cos A\sin B$ $\cdots (4\ast)$
$(3\ast)-(4\ast)$を計算します.
$\sin(A+B)-\sin(A-B)=2\cos A\sin B$ $\cdots (\clubsuit)$
$(\clubsuit)$の左辺と$(2\sharp)$の左辺との対応関係を書き出しましょう.
$A+B= \theta+\delta +\alpha$ $\cdots (10\ast)$
$A-B= \theta -\alpha $ $\cdots (11\ast)$
$(10\ast)+(11\ast)$を計算し,$A$を求めます.
$2A=2\theta+\delta$
$\therefore A=\theta+\dfrac{\delta}{2}$ $\cdots (12\ast)$
$(10\ast)-(11\ast)$を計算し,$B$を求めます.
$2B=\delta+2\alpha$
$\therefore B=\alpha+\dfrac{\delta}{2}$ $\cdots (13\ast)$
$(12\ast)$,$(13\ast)$を$(\clubsuit)$の右辺に代入して積の形をつくります.
$\sin(\theta+\delta+\alpha)-\sin(\theta-\alpha)=2\cos\left(\theta+\dfrac{\delta}{2}\right)\sin\left(\alpha+\dfrac{\delta}{2}\right)$
よって,$(2\sharp)$の式は
$2\cos\left(\theta+\dfrac{\delta}{2}\right)\sin\left(\alpha+\dfrac{\delta}{2}\right)=0$
$\therefore\,\,\, \cos\left(\theta+\dfrac{\delta}{2}\right)=0 $または $\sin\left(\alpha+\dfrac{\delta}{2}\right)=0$
しかし,重ならないときを考えるので,整数$n’$を用いて
$\theta+\delta+\alpha\neq\theta-\alpha+2\pi n’$
$\therefore\,\,\,\alpha+\dfrac{\delta}{2}\neq\pi n’$
より, $\sin\left(\alpha+\dfrac{\delta}{2}\right)\neq 0$となる.よって,$y=\sin\left(\theta-\alpha\right)$と$y=\sin\left(\theta+\delta+\alpha\right)$の交点の$\theta$座標を$\theta_{0}’$とすると,$\theta_{0}’$は次の式を満たす.
$\cos\left(\theta_{0}’+\dfrac{\delta}{2}\right)=0$ $\cdots (14\ast)$
結論
$(9\ast)$と$(14\ast)$は同じ式なので,交点の$\theta$座標は変化しないことがわかる.($\pm 2\pi,\pm 4\pi,\cdots$分ずれているかもしれないが,見かけ上は変化してない)

このことから,速さ,波長,振幅が同じで逆向きに進行する正弦波の交点の横座標は変化しないことがわかります.
この交点はそれぞれの媒質の振動のタイミング(位相)が同じことから大きな振幅で振動する腹となるわけです.


コメント