
コンデンサー2つを並列に結んだ回路とコイルをつなげる問題はどのように考えればいいだろう??

コンデンサーを並列合成して考えていくと,こちらでやった$LC$振動回路の基本形と同じように考えることができます.
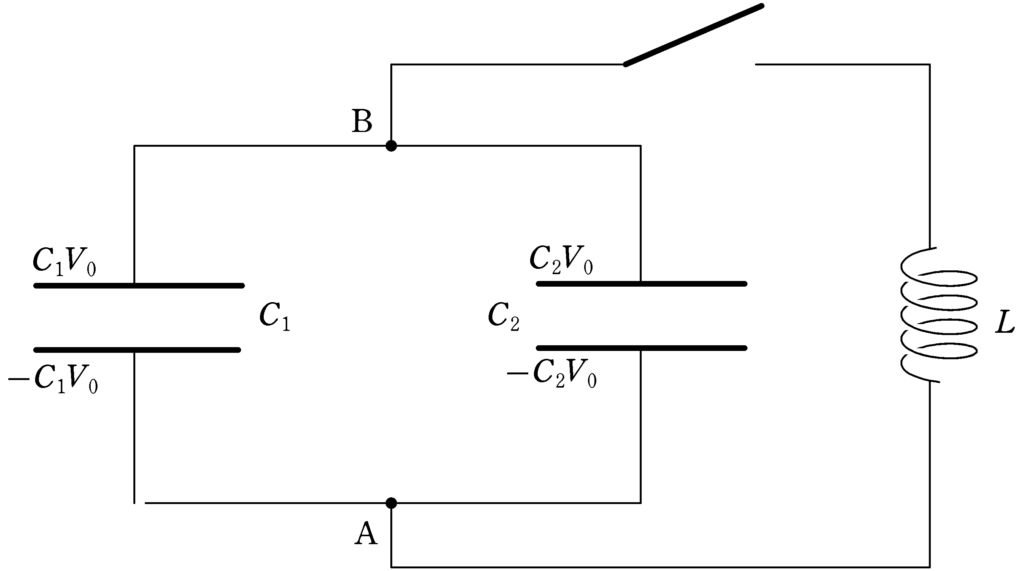

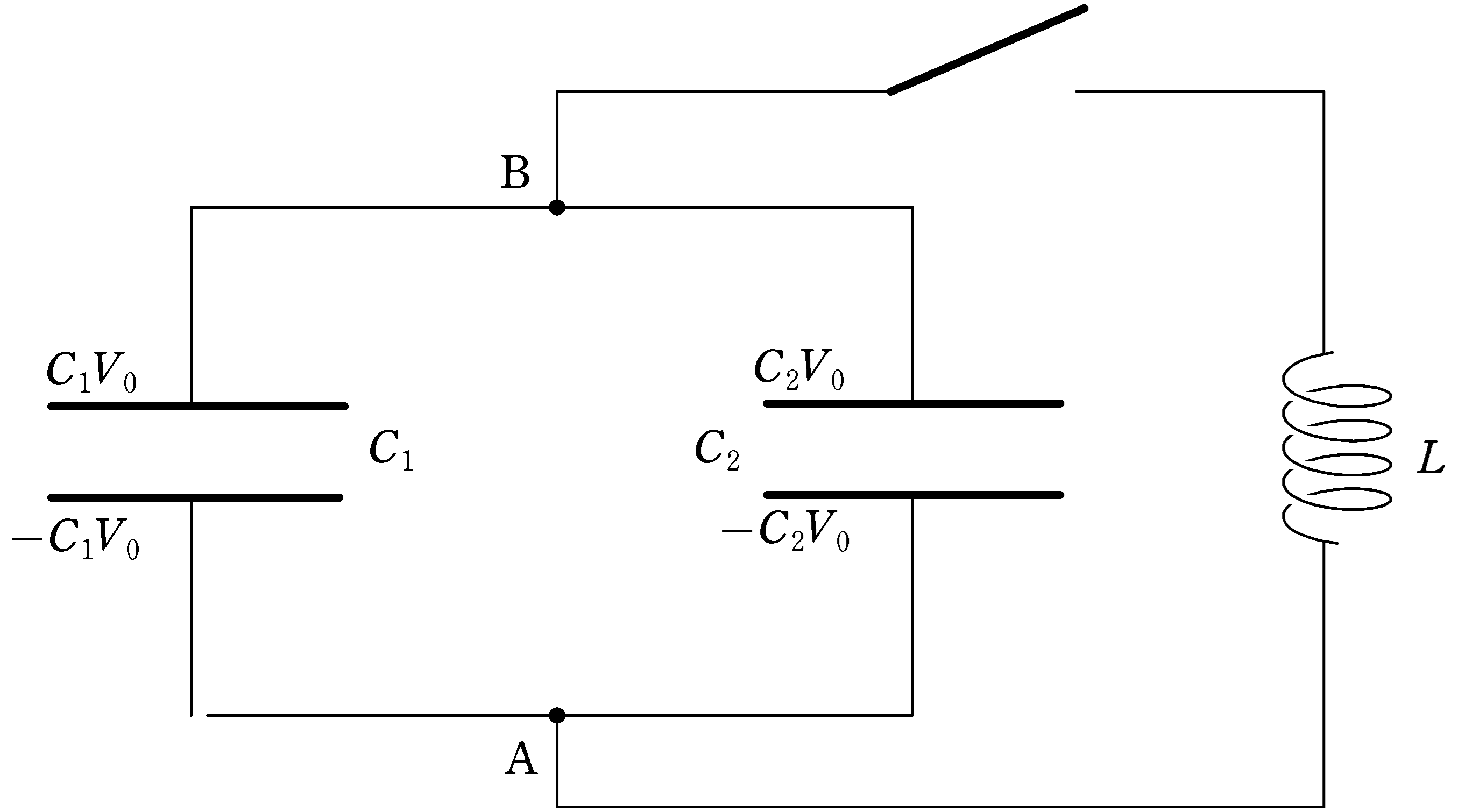
あらかじめ,電気容量$C_{1} , C_{2}$のコンデンサーに起電力$V_{0}$の電池につないでそれぞれ$C_{1}V_{0} , C_{2}V_{0}$の電荷が蓄えられている状態からスイッチを閉じて,コイルに流れる電流や上図のAに対するBの電位の時間変化を考えていきましょう.

たしか,並列合成していいっていってたよね.
でも,容量$C_{1}$と$C_{2}$に流れる電流のタイミングって本当に一致するのかな??

それを確かめるために微分方程式を立ててみましょう.
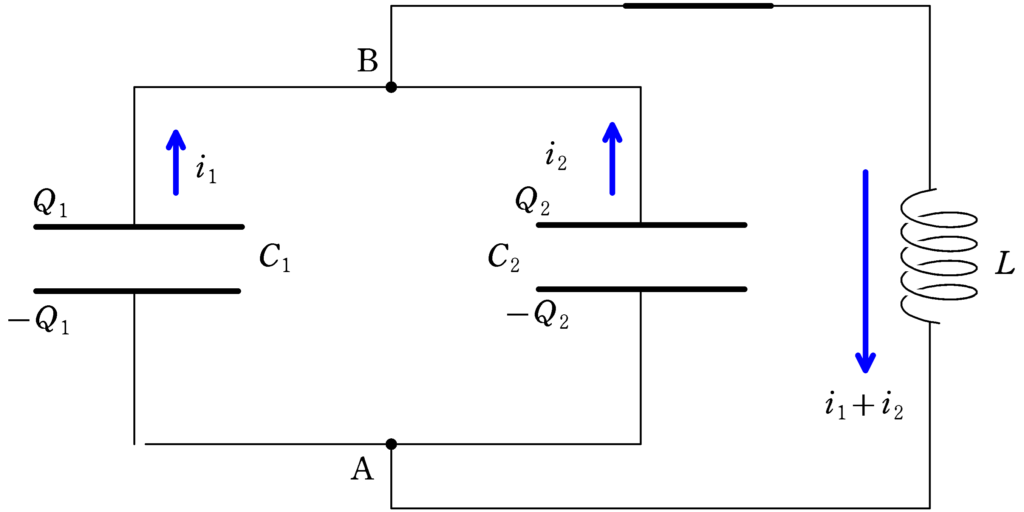

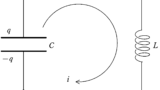
時刻$t=0$でスイッチを閉じましょう.時刻$t$における,容量$C_{1} , C_{2}$に蓄えられる電荷をそれぞれ$Q_{1} , Q_{2}$としましょう.(上側極板の電荷を+としましょう.)
さらに,上図の向きに電流$i_{1} , i_{2}$に流れていると,キルヒホッフ第1法則より,コイルには$i_{1}+i_{2}$の電流が流れます.
$C_{1} , C_{2}$のコンデンサーおよびコイルの電圧がすべて等しいことから,Aに対するBの電位に関する微分方程式をつくってみましょう.
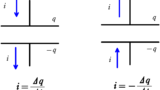
電流の定義式の正負についてはこちら.
★ コンデンサーの式
Aに対するBの電位を$V$とする.
$Q_{1}=C_{1}V$ , $Q_{2}=C_{2}V$ $\dots (\ast)$
★ 電流の定義式
$i_{1}=-\dfrac{dQ_{1}}{dt}$ $\dots (2\ast)$
$i_{2}=-\dfrac{dQ_{2}}{dt}$ $\dots (3\ast)$
$(\ast)$を,$(2\ast)$,$(3\ast)$に代入して
$i_{1}=-C_{1}\dfrac{dV}{dt}$ $\dots (4\ast)$
$i_{2}=-C_{2}\dfrac{dV}{dt}$ $\dots (5\ast)$
★ キルヒホッフ則(A→$C_{1}$の方のコンデンサー→コイル)
$V-L\dfrac{d}{dt}\left(i_{1}+i_{2}\right)=0$
$(4\ast)$,$(5\ast)$を上式に代入して
$V-L\left( -C_{1}\dfrac{dV}{dt} -C_{2}\dfrac{dV}{dt} \right)=0$
$\therefore L(C_{1}+C_{2})\dfrac{d^{2}V}{dt^{2}}=-V$

ここで,$C=C_{1}+C_{2}$とおいて,両辺$C$で割ると
$L\dfrac{d^{2}V}{dt^{2}}=-\dfrac{V}{C}$

これは,単振動の運動方程式
$ma=-kx$
の形になっているね.加速度は位置$x$の2階微分だから
$a=\dfrac{d^{2}x}{dt^{2}}$
なので,
$m\dfrac{d^{2}x}{dt^{2}}=-kx$
この単振動の角振動数$\omega$は
$\omega=\sqrt{\dfrac{k}{m}}$
だったね.
単振動を忘れてしまった人は,こちらのシリーズで演習問題があるので,確実に解けるようにしておこう.
これと比較すると
$\omega=\dfrac{1}{\sqrt{LC}}$
です.

さらに,$C=C_{1}+C_{2}$は並列合成の式だったんだね.
1.直列合成
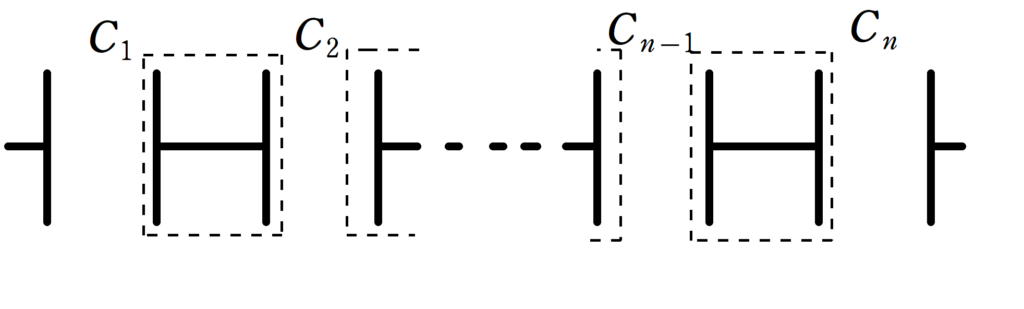
電気容量$C_{1}$,$C_{2}$,$\dots$,$C_{n-1}$,$C_{n}$の$n$個のコンデンサーを直列に結ぶ.
上図のように,点線で囲まれた各部分の電荷の和が0のとき,この$n$個のコンデンサーの合成容量$C$は次のような関係式を満たす.
$\dfrac{1}{C}=\dfrac{1}{C_{1}}+\dfrac{1}{C_{2}}+\dots +\dfrac{1}{C_{n-1}}+\dfrac{1}{C_{n}}$
2.並列合成
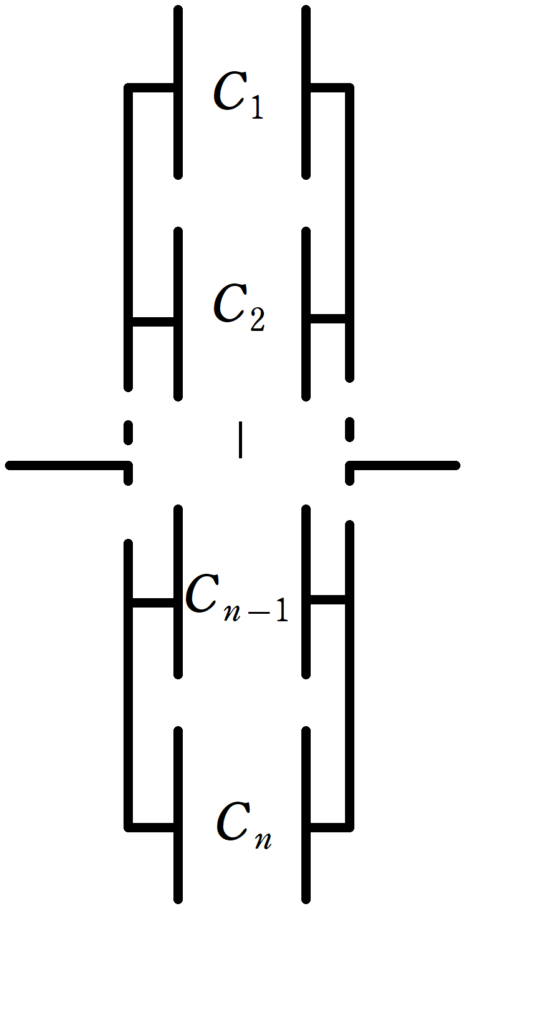
電気容量$C_{1}$,$C_{2}$,$\dots$,$C_{n-1}$,$C_{n}$の$n$個のコンデンサーを直列に結ぶ.
この$n$個のコンデンサーの合成容量$C$は次のような関係式を満たす.
$C=C_{1}+C_{2}+\dots +C_{n-1}+C_{n}$

Aに対するBの電位は$t=0$で$V_{0}$で,次の瞬間電位が下がるので,$\cos$型です.
したがって
$V=V_{0}\cos(\omega t)$
です.
すると,$(\ast) , (2\ast)$より
$Q_{1}=C_{1}V_{0}\cos(\omega t)$
$Q_{2}=C_{2}V_{0}\cos(\omega t)$
になり,さらに,
$\eqalign{\dfrac{dV}{dt}&=\dfrac{d}{dt}\left(V_{0}\cos(\omega t)\right)&=-V_{0}\omega \sin(\omega t)}$
なので,$(4\ast)$,$(5\ast)$より
$i_{1}=C_{1}V_{0}\omega \sin(\omega t)$
$i_{2}=C_{2}V_{0}\omega\sin(\omega t)$
となり,電気容量$C_{1} , C_{2}$に流れる電流のタイミングは全く同じとなります.

そもそも容量$C_{1} , C_{2}$にかかる電圧のタイミングが同じなので,コンデンサーの基本式より,電荷の時間変化のタイミングも同じだし,流れる電流のタイミングも同じなんだね.
だから,コンデンサーを並列合成して考えてもいいということなんだね.




コメント