
前回,LC振動回路を扱って,電荷や電流,電位が単振動($\sin$や$\cos$の時間変化)をすることを確認したね.
コンデンサー2つを直列に結んだ場合はどうなるんだろう??
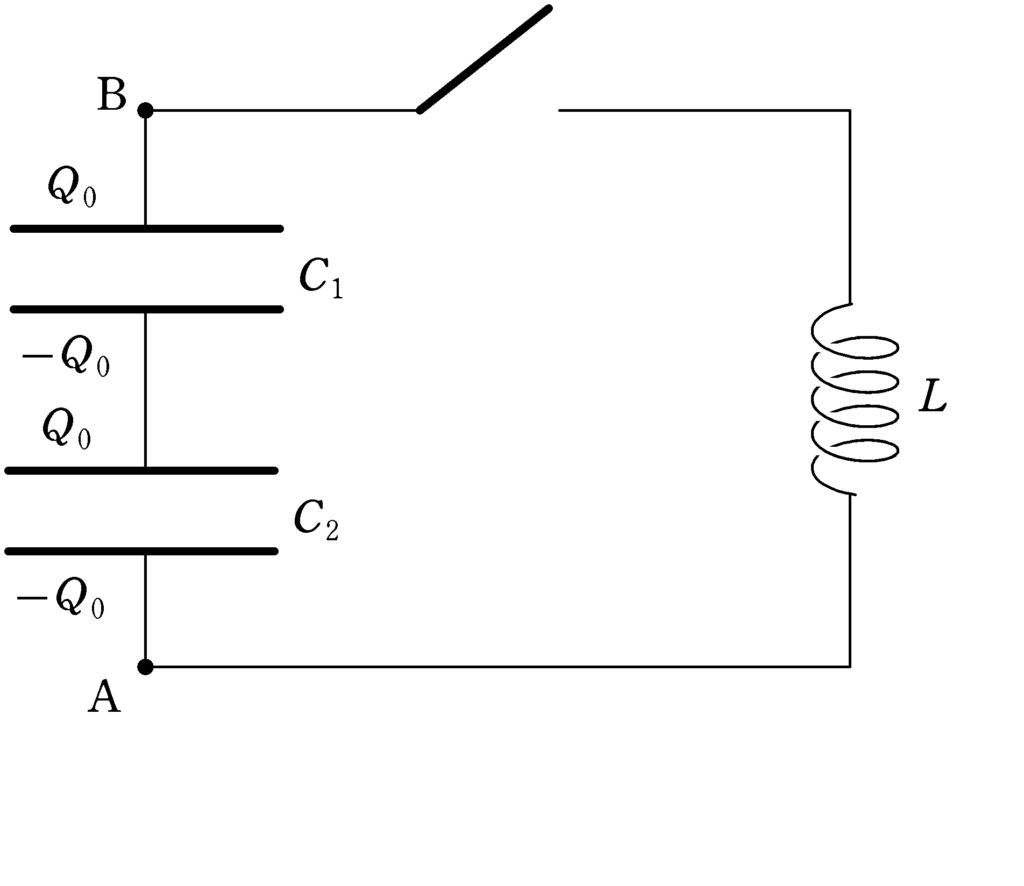

入試問題では,コンデンサーを直列合成して解くことが多いですね.
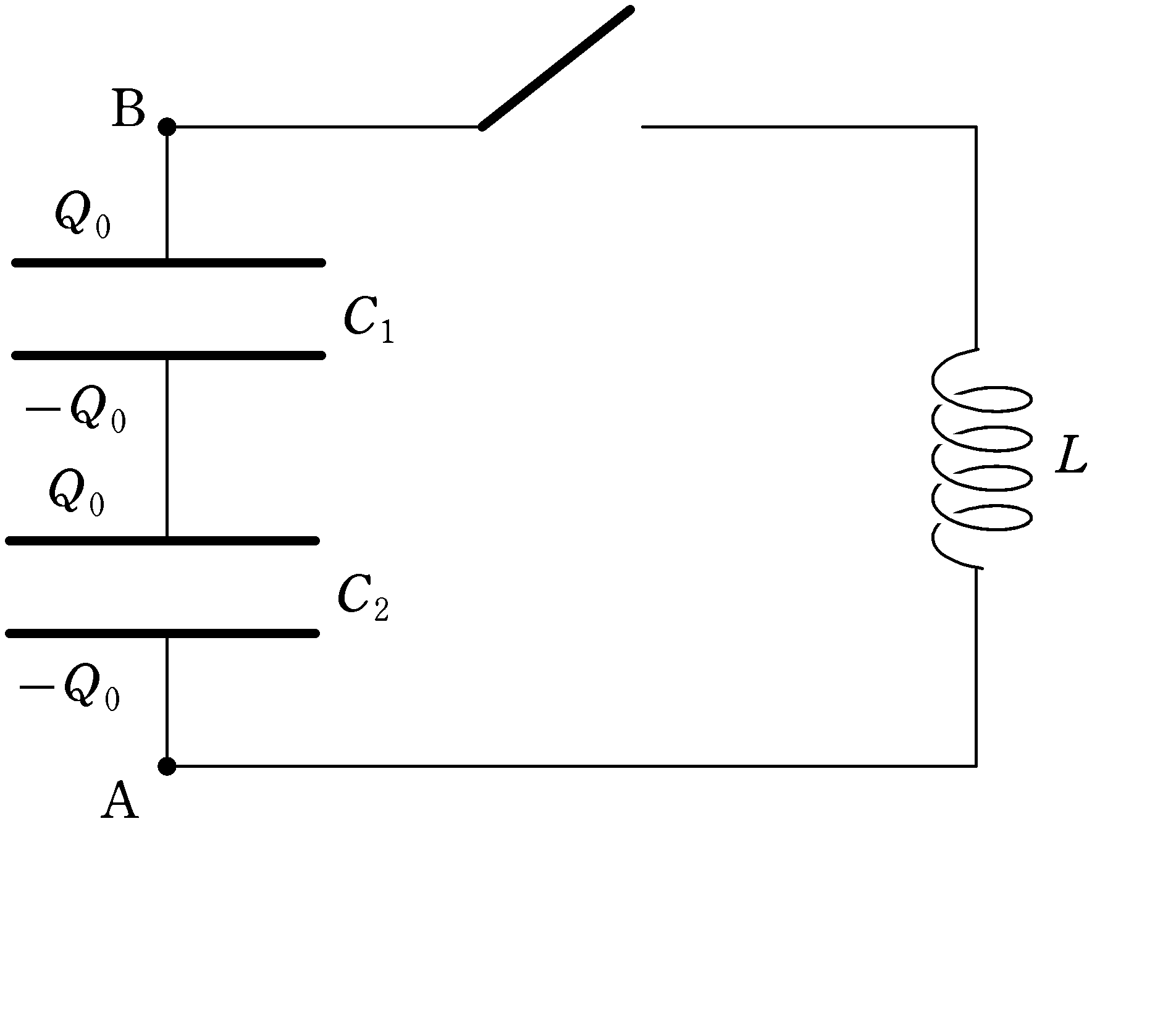
ただし,入試問題では2つのコンデンサーの間の電荷の和が0の場合とそうでない場合があります.今回は,上図のように,電荷の和が0の場合についてです.
直列合成すると,前回の内容と同様に考えることができます.
1.直列合成
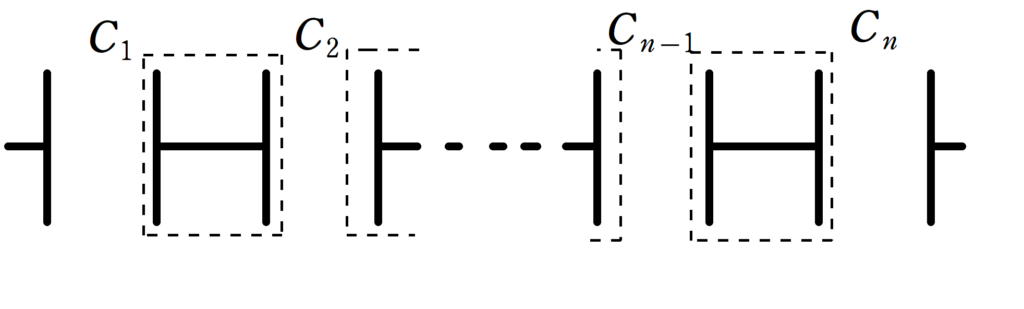
電気容量$C_{1}$,$C_{2}$,$\dots$,$C_{n-1}$,$C_{n}$の$n$個のコンデンサーを直列に結ぶ.
上図のように,点線で囲まれた各部分の電荷の和が0のとき,この$n$個のコンデンサーの合成容量$C$は次のような関係式を満たす.
$\dfrac{1}{C}=\dfrac{1}{C_{1}}+\dfrac{1}{C_{2}}+\dots +\dfrac{1}{C_{n-1}}+\dfrac{1}{C_{n}}$
2.並列合成
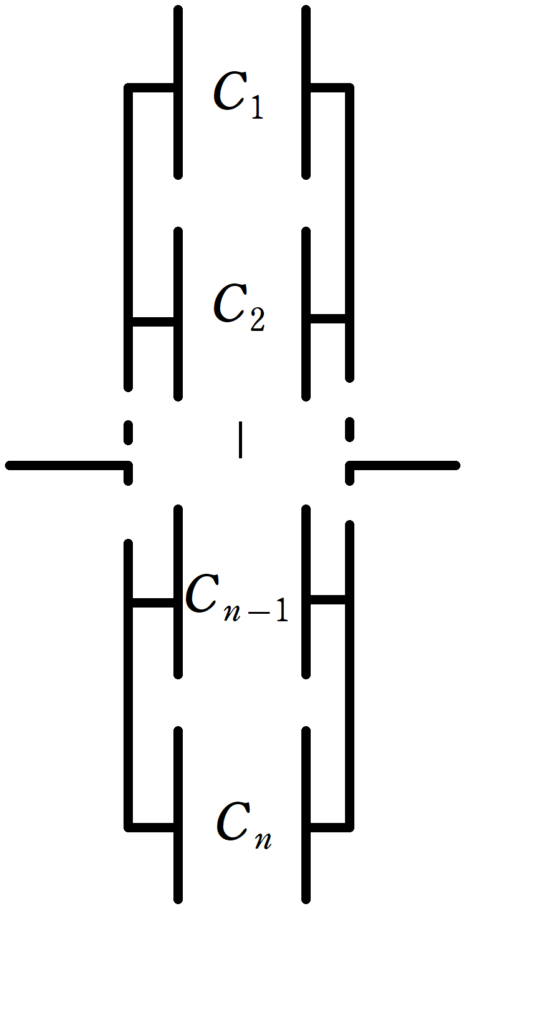
電気容量$C_{1}$,$C_{2}$,$\dots$,$C_{n-1}$,$C_{n}$の$n$個のコンデンサーを直列に結ぶ.
この$n$個のコンデンサーの合成容量$C$は次のような関係式を満たす.
$C=C_{1}+C_{2}+\dots +C_{n-1}+C_{n}$

つまり,2つのコンデンサーの電気容量を$C_{1} , C_{2}$として,合成容量を$C$とすると
$\eqalign{\dfrac{1}{C}=\dfrac{1}{C_{1}}+\dfrac{1}{C_{2}}\cr C=\dfrac{C_{1}C_{2}}{C_{1}+C_{2}}}$
なので,角振動数$\omega=\dfrac{1}{\sqrt{LC}}=\sqrt{\dfrac{C_{1}+C_{2}}{LC_{1}C_{2}}}$で,振動の周期$T$は
$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{LC_{1}C_{2}}{C_{1}+C_{2}}}$
だね.
そして,2つのコンデンサーの電圧を$V$,回路に流れる電流を$i$として,
$\dfrac{1}{2}\cdot \dfrac{C_{1}C_{2}}{C_{1}+C_{2}}V^{2}+\dfrac{1}{2}Li^{2}=$一定
が成り立つんだね.

そうですね.
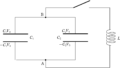
ちなみに,下図の状態から,スイッチを閉じた瞬間を時刻$t=0$として,時刻$t$において,容量$C_{1}$および$C_{2}$のCに対するBの電位を$V_{1}$,Cに対するAの電位を$V_{2}$,蓄えている電荷を$q_{1}$,$q_{2}$,回路に流れる電流を$i$とします.
NEKOさんがおっしゃったように,角振動数は$\omega= \sqrt{\dfrac{C_{1}+C_{2}}{LC_{1}C_{2}}} $で,はじめに蓄えられている電荷を$Q_{0}$とすると
$q_{1}=Q_{0}\cos \omega t$
$q_{2}=Q_{0}\cos \omega t$
$i=i_{0}\sin \omega t$
$V_{1}=\dfrac{Q_{0}}{C_{1}}\cos \omega t$
$V_{2}=\dfrac{Q_{0}}{C_{2}}\cos \omega t$
となります.$i_{0}$はエネルギー保存則で求めることができます.
電流の大きさが最大になるときは,コンデンサーの電圧(電荷)は0なので
$\dfrac{1}{2}Li_{0}^{2}=\dfrac{Q_{0}^{2}}{2C}$
$i_{0}=Q_{0}\sqrt{\dfrac{1}{LC}}$

コンデンサーを合成してしまえば,コンデンサーが1つの場合と同じように考えることができるんだね.
ところで,微分方程式でかくとどうなるんだろう??

では,式を立ててみましょう.
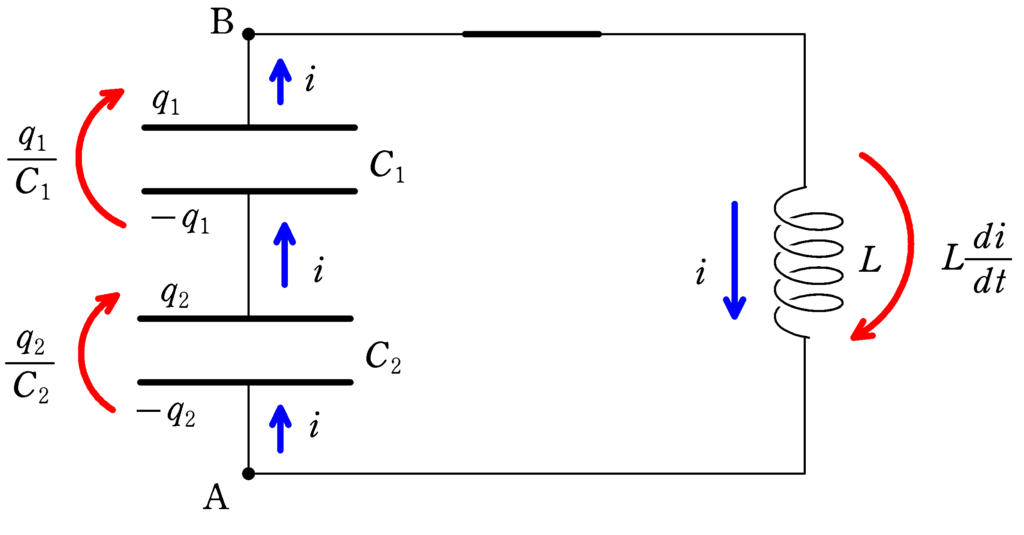
★ コンデンサーの基本式
$q_{1}=C_{1}V_{1}$ $\dots (\ast)$
$q_{2}=C_{2}V_{2}$ $\dots (2\ast)$
★ 電荷保存則
$-q_{1}+q_{2}=0$ $\therefore q_{1}=q_{2}$ $\dots (3\ast)$
$(3\ast)$より,$q_{1}=q_{2}=q$$\dots (4\ast)$とおく
★ キルヒホッフ則
$\dfrac{q_{1}}{C_{1}}+\dfrac{q_{2}}{C_{2}}-L\dfrac{di}{dt}=0$
$(4\ast)$より
$\dfrac{q}{C_{1}}+\dfrac{q}{C_{2}}-L\dfrac{di}{dt}=0$

この式で$\dfrac{1}{C}=\dfrac{1}{C_{1}}+\dfrac{1}{C_{2}}$とおけば,こちらの記事の$(2\ast)$と同じ式になるんだね.

そうですね.つまり,この先は計算しなくとも,合成してしまえば,同じ結果になることがわかるはずです.
初期状態において,電荷の和が0の場合,コンデンサーの直列合成をして問題を解く.合成容量を$C$,コイルの自己インダクタンスを$L$と,次の3つをおさせる.
1. 角振動数$\omega$は,$\omega=\dfrac{1}{\sqrt{LC}}$
2. 電流の大きさが最大のとき,電荷が0.電荷がが最大のとき,電流は0
3. $\dfrac{1}{2}CV^{2}+\dfrac{1}{2}Li^{2}=$一定が成り立つ.

コメント