
今回は,高校物理で出てくる運動方程式の形を
まとめましょう.
運動方程式の形を知っておくことで次のようなメリットがあります.
- 各運動の特徴を知ることができる.
- 運動の全体像を把握することができる.
以下,質量を$m$,加速度を$a$,座標を$x$,速度を$v$,定数を$C$,正の比例定数を$k$,中心力を$\vec{C}$とする.
① $ma=C$
等加速度運動
② $ma=-kx+C$
単振動
③ $ma=-kv+C$
終端速度型の運動
※$+\alpha$ $m\vec{a}=\vec{C}$
円運動(今回は扱いません)
$ma=C$ 等加速度運動

$ma=$定数の形だね.
等加速度運動であることを確認できたら,次の3つの式を使うことができるよ.
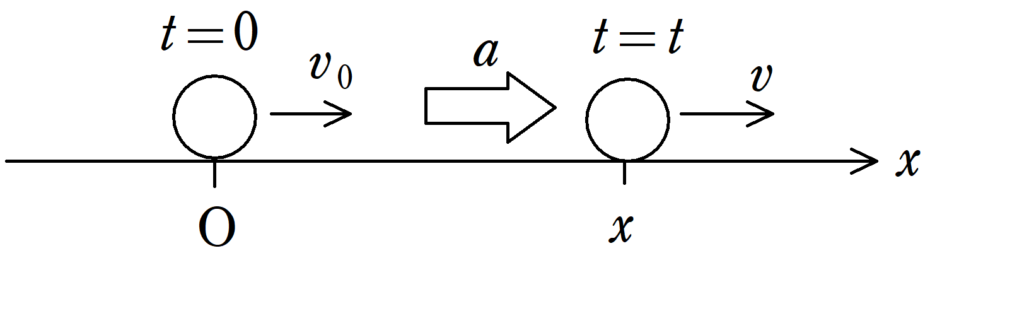
物体は加速度$a$で$x$軸上を運動している.$t=0$において,原点にある物体が,時刻$t$に座標$x$に移動した.初速度を$v_{0}$,時刻$t$における速度を$v$とするとき,次の関係式が成り立つ.
$v=v_{0}+at$ $\dots (\ast)$
$x=v_{0}t+\dfrac{1}{2}at^2$ $\dots (2\ast)$
$v^{2}-v_{0}^{2}=2ax$ $\dots (3\ast)$

$x$は距離ではなく座標だったね.
距離と座標が等しいときもあるけど,そうではないときに間違わないように,普段から座標を意識しょう.
なぜ,$x$は距離ではなく座標なのかを知りたい方は下記の記事を読んでみてください.
$\clubsuit$準備$\clubsuit$
- 時間$\Delta t$の間に速度が$\Delta t$変化したときの加速度$a$は$a=\dfrac{\Delta v}{\Delta t}$
- 縦軸を$v$(速度),横軸を$t$としたグラフの傾きは加速度,面積は移動距離を表す.
$\spadesuit$導出$\spadesuit$

上図のように,時刻$t=0$で初速$v_{0}$,座標$x=0$にあった物体が等加速度運動をしている.
時刻$t$において,速度が$v$,座標が$x$であるとする.
●$v=v_{0}+at$の式
加速度の定義式より
$a=\dfrac{\Delta v}{\Delta t}=\dfrac{v-v_{0}}{t-0}$
$\therefore v=v_{0}+at$
●$x=v_{0}+\dfrac{1}{2}at^2$の式
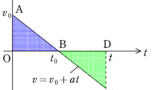
上式を$v-t$グラフにかくと次のようになる.
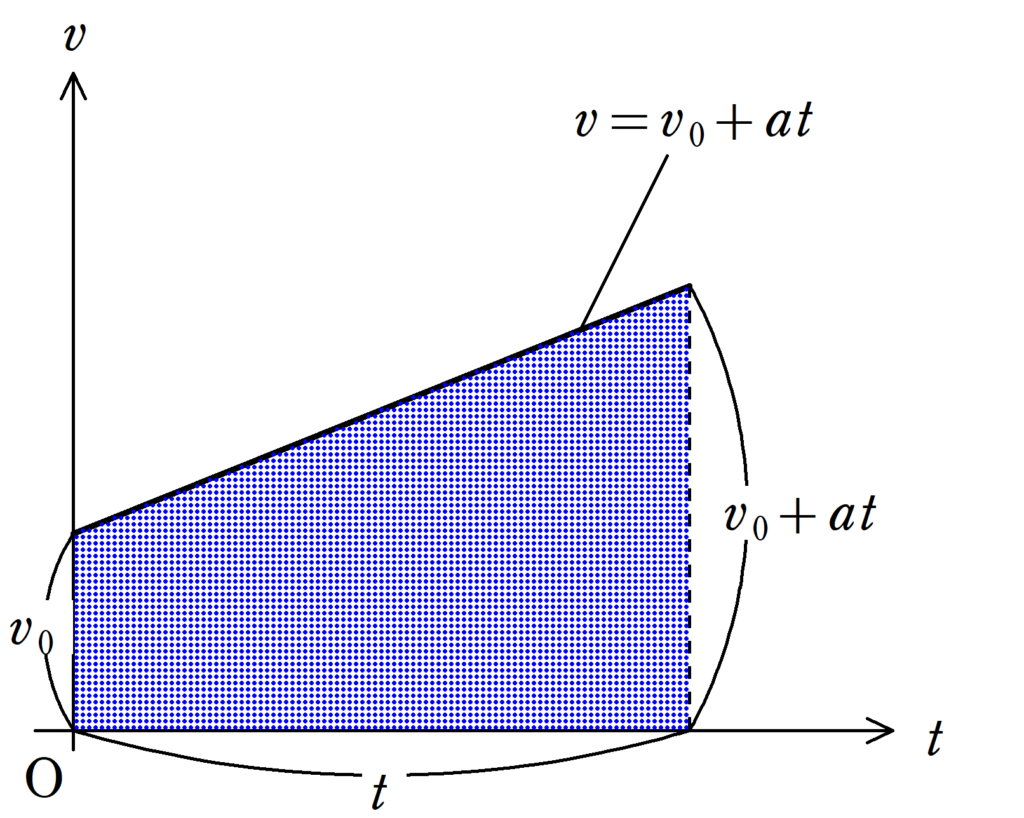
この台形の面積が移動距離に等しく,座標が常に正にありかつ正の方向に速度をもっていれば移動距離と座標が一致する.今回はこの場合だけ計算する.
台形の面積を求めて
$x=(v_{0}+v_{0}+at)\cdot t\cdot \dfrac{1}{2}$=$v_{0}t+\dfrac{1}{2}at^2$
●$v^{2}-v_{0}^{2}=2ax$の式
$(\ast)$の式より
$t=\dfrac{v-v_{0}}{a}$
これを$x=v_{0}t+\dfrac{1}{2}at^2$に代入して$t$を消去すると
$\eqalign{x&=v_{0}t+\dfrac{1}{2}at^{2}\\&=v_{0}\cdot \dfrac{v-v_{0}}{a}+\frac{1}{2}a\cdot(\dfrac{v-v_{0}}{a})^{2}\\&=\dfrac{v_{0}v-v_{0}^{2}}{a}+\dfrac{v^{2}-2vv_{0}+v_{0}^{2}}{2a}\\&=\dfrac{v^{2}-v_{0}^{2}}{2a}}$
両辺$2a$をかけて
$v^{2}-v_{0}^{2}=2ax$
$ma=-kx+C$ 単振動

単振動に関しては,こちらで解説+演習を扱っているよ.

単振動の運動方程式は一般的に次のような形になります.
$ma=-kx+C=-k(x-\dfrac{C}{k})$
$x_{0}=\dfrac{C}{k}$とおくと
$ma=-k(x-x_{0})$
となります.
運動方程式から次のような情報を得ることができます.
質量を$m$,加速度を$a$,座標を$x$,正の定数を$k$,定数を$x_{0}$とすると,単振動の運動方程式は
$ma=-k(x-x_{0})$
このとき,次の情報を読み取ることができる.
- 振動の中心$x=x_{0}$
- 角振動数$\omega=\sqrt{\dfrac{k}{m}}$
- 振動の周期$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{m}{k}}$
また,単振動の振幅を$A$,初期位相を$\phi$とすると,座標$x$と時間の関係は次のようになる.
$x=x_{0}+A\sin(\omega t+\phi)$
$ma=-kv+C$ 終端速度型の運動

空気抵抗がある場合の運動や,導体棒の運動などで出てくるね.

この形は次の3つのポイントをおさえましょう.
- 十分時間が経つと速度が一定になる.(加速度が0)
- 終端速度は$\dfrac{C}{k}$
- $t=0$のときの加速度を求めさせることが多い.
まとめると,次のようになります.
質量を$m$,加速度を$a$,速度を$v$,$C$を定数とすると
$ma=-kv+C$
は終端速度型の運動方程式である.
終端速度型の運動方程式は次の特徴がある.
十分時間が経つと,速度が一定(加速度が0)になる.
速度が一定になったときの速度を終端速度という.
終端速度は運動方程式に$a=0$を代入して
$0=-kv+C$ $\therefore v=\dfrac{C}{k}$
また,$t=0$のときの速度を$v_{0}$とすると,そのときの加速度($v-t$グラフの傾き)は
$a=\dfrac{-kv_{0}+C}{m}$
となる.

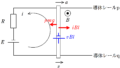
たとえば,次のような空気抵抗がはたらく場合について考えてみよう.
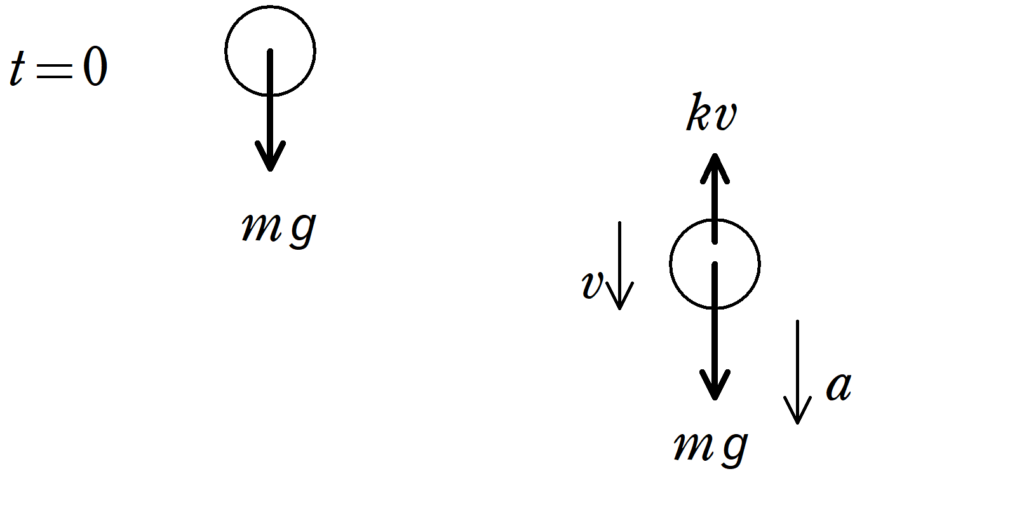

$t=0$で物体が初速度0で運動を開始します.
その後,物体が速度をもつと,速さに比例した空気抵抗がはたらきます.
速さが$v$のときの空気抵抗の大きさは,比例定数$k$を用いて,$kv$で,向きは速度と逆向きです.
座標の向きと加速度の向きを鉛直下向きにとりましょう.
加速度を$a$と設定して,運動方程式を立てると,次のようになります.
$ma=-kv+mg$

はじめ,$v=0$からスタートするので,加速度は$a=g$です.
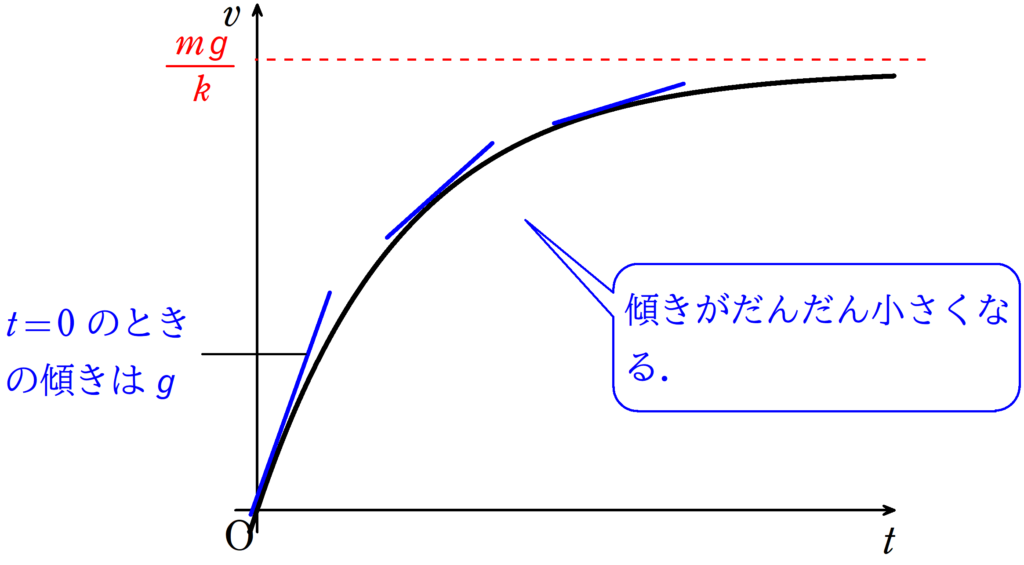
$v-t$グラフの傾きは加速度でした.
なので,はじめの傾きは$g$です.
しかし,少しずつ$v$が大きくなっていくことで,運動方程式の右辺である$-kv+mg$が小さくなります.
つまり,左辺の加速度$a$が小さくなります.
これは,$v-t$グラフの傾きがだんだんと小さくなっていくことを意味しています.
そして,最終的には,$-kv+mg=0$となり,加速度が0になります.
つまり,$v-t$グラフの傾きが0になって,以後,速度は変化しません.
このときの速度は
$-kv+mg=0$ $\therefore v=\dfrac{mg}{k}$
です.終端速度は$v=\dfrac{mg}{k}$となります.
$ma=-kv+mg$の運動方程式をきちんと解くと次のようになります.
$a=\dfrac{dv}{dt}$
より,
$m\dfrac{dv}{dt}=-k(v-\dfrac{mg}{k})$
$\dfrac{mg}{k}$は$t$によらない定数なので,$\dfrac{dv}{dt}=\dfrac{d}{dt}(v-\dfrac{mg}{k})$より
$m\dfrac{d}{dt}(v-\dfrac{mg}{k})=-k(v-\dfrac{mg}{k})$
ここで,$V=v-\dfrac{mg}{k}$として
$m\dfrac{dV}{dt}=-kV$
変数分離をして
$\dfrac{1}{V}\dfrac{dV}{dt}=-\dfrac{k}{m}$
両辺$t$で積分をすると
$\displaystyle{\int{\dfrac{1}{V}\dfrac{dV}{dt}}dt=-\dfrac{k}{m}\int dt +C}$
ただし,$C$は積分定数です.積分を計算すると
$\displaystyle{\int{\dfrac{1}{V}}dV=-\dfrac{k}{m}t+C}$
$\therefore \log{|V|}=-\dfrac{k}{m}t+C$
これを$V$について解きます.
$|V|=e^{-\frac{k}{m}t+C}=e^{C}\cdot e^{-\frac{k}{m}t}$
$V=v-\dfrac{mg}{k}$ともどして,$V<0$であることから,$|V|=-v+\dfrac{mg}{k}$として,
$-v+\dfrac{mg}{k}=e^{C}\cdot e^{-\frac{k}{m}t}$ $\dots (\ast)$
$t=0$のとき,$v=0$なので
$\dfrac{mg}{k}=e^{C}$
これを$(\ast)$に代入して
$v=\dfrac{mg}{k}-\dfrac{mg}{k}e^{-\frac{k}{m}t}=\dfrac{mg}{k}(1-e^{-\frac{k}{m}t})$

以上です.
最後にそれぞれの運動の大事なポイントをまとめておきます.
まとめ
① $ma=C$ 等加速度運動
等加速度運動の式
$v=v_{0}+at$
$x=v_{0}t+\dfrac{1}{2}at^2$
$v^{2}-v_{0}^{2}=2ax$
を立てて解く.
② $ma=-kx+C$ 単振動
$ma=-k(x-x_{0})$と変形して,中心$x=x_{0}$と角振動数$\omega=\sqrt{\dfrac{k}{m}}$と周期$T=2\pi \sqrt{\dfrac{m}{k}}$を求める.
次に,初期条件から振幅や初期位相を求める.
③ $ma=-kv+C$ 終端速度型
十分時間が経つと,速度が一定になると覚えておく.
つまり,終端速度は$a=0$のときで$v=\dfrac{C}{k}$
また,$t=0$の加速度をきかれることも多いので,運動方程式に代入して計算する.




コメント
[…] 高校物理出てくる運動方程式3つ!+αPHYさん今回は,高校物理で出てくる運… […]
[…] 高校物理出てくる運動方程式3つ!+αPHYさん今回は,高校物理で出てくる運… […]
[…] 高校物理出てくる運動方程式3つ!+αPHYさん今回は,高校物理で出てくる運… 終端速度型の運動方程式 […]
[…] 高校物理出てくる運動方程式3つ!+α […]