[等加速度運動の式]$x=v_{0}t+\dfrac{1}{2}at^2$の$x$は移動距離ではなく座標！

図1のように，$t=0$において原点に物体があり，このときの速度が$v_{0}$であるとします．ここから等加速度直線運動をし，時刻$t$における速度が$v$，座標を$x$とするとき，次の関係式が成り立つことが知られています．

$v=v_{0}+at$　$\dots (\ast)$

$x=v_{0}t+\dfrac{1}{2}at^2$　$\dots (2\ast)$　

$x$は”座標”と書きましたが，これを”移動距離”と勘違いして解く人がときどきいるようです．確かに，移動距離として考えてもたまたま解けることはありますが，特別な場合だけを覚えているといざというときに困ります．そこで今回は$x$が移動距離ではなく，座標（$t=0$にあった場所からの変位）であることを確認していきたいと思います．

　$x=v_{0}t+\frac{1}{2}at^2$ の導出

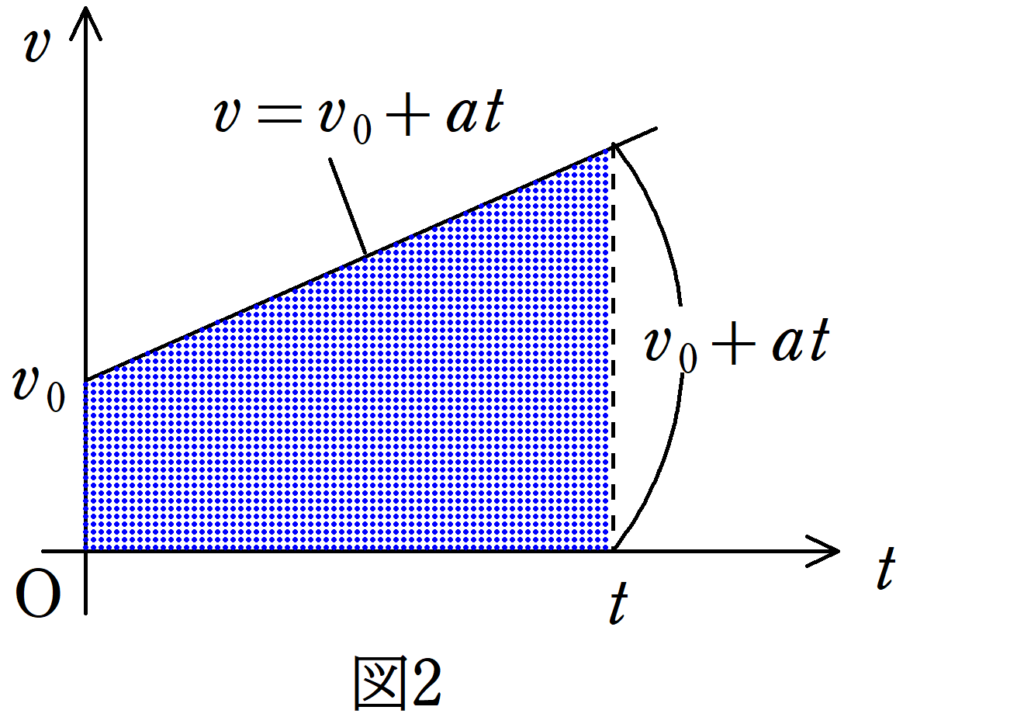
速さ$v$で$\Delta t$の間に動く距離は$v \Delta t$です．これはちょうど縦軸が$v$，横軸が$t$の$v-t$グラフにおける長方形の面積に対応します．この長方形の面積を細かく計算すると，結局$v-t$グラフの直線と$t$軸で囲まれた青い部分の面積となります．

台形の面積$=\{v_{0}+(v_{0}+at)\}\cdot t \cdot \dfrac{1}{2} =v_{0}t+\dfrac{1}{2}at^2$

これをみると，”結局$x=v_{0}t+\dfrac{1}{2}at^2$は距離の式じゃないか”と思うかもしれません．しかし，これはたまたまです．たとえば，$x=5$における原点からの移動距離は5であることと同じです．

　$x$は座標を表す理由

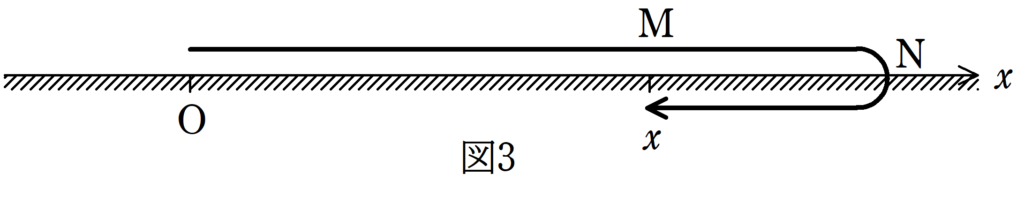
図3のように，Oから出発し，Mを経由し，Nで折り返して，Mに戻ってくる運動を考えてみましょう．

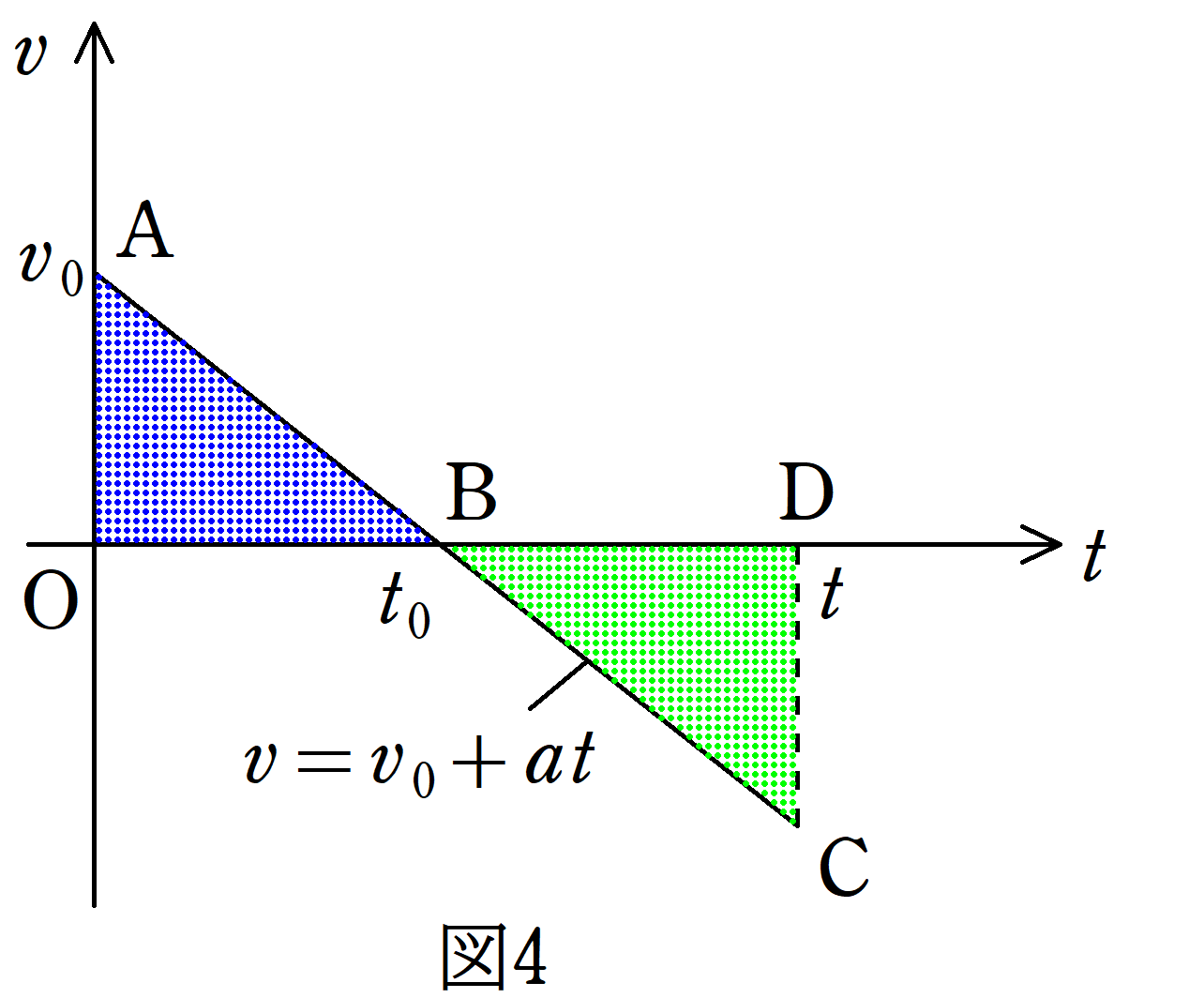
$x=v_{0}t+\dfrac{1}{2}at^2$が移動距離を表すのであれば，O-M-N-Mの総合の距離を表すはずです．ところで，このような等加速度運動になるのは，Oから速度がだんだんと小さくなっていき，Nで速度が0になり，負の速度になる必要があります．一番有名な例では鉛直投げ上げ運動ですね．このときの$v-t$グラフは図4のようになります．

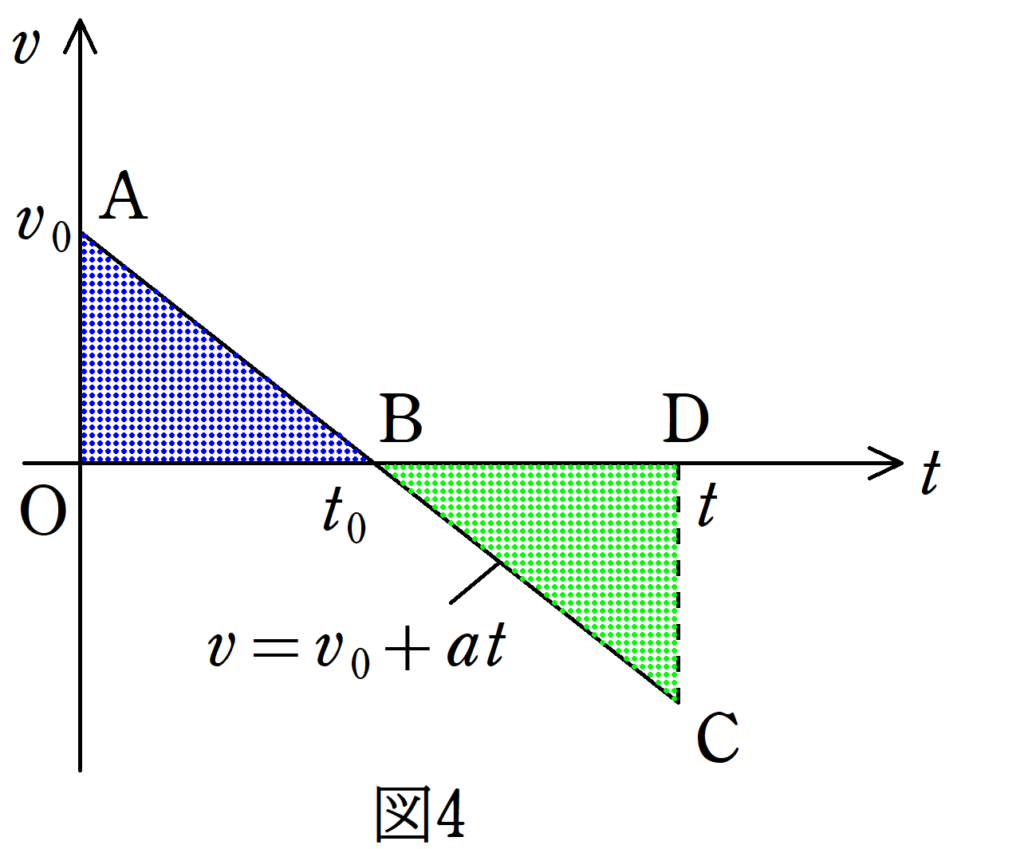
図4の$t=t_{0}$でNに達します．$t=t_{0}$は速度$v=0$であるときなので，($\ast$)より

$0=v_{0}+at_{0}$

$\therefore t_{0}=-\dfrac{v_{0}}{a}$

となります．O-M-Nの距離が青い三角形の面積であり，N-Mの距離が緑の三角形の面積となります．これらの和がO-M-N-Mの総合の距離です．それでは計算してみましょう．総合の距離を$L$として

$\eqalign{L&=\dfrac{1}{2}t_{0}v_{0}+\dfrac{1}{2}(t-t_{0})\cdot |v_{0}+at| \\&=\dfrac{1}{2}(-\dfrac{v_{0}}{a})v_{0}+\dfrac{1}{2}(t-(-\dfrac{v_{0}}{a}))(-v_{0}-at)\\&= -\dfrac{v_{0}^2}{2a}-\dfrac{1}{2}(t+\dfrac{v_{0}}{a})(v_{0}+at)\\&=-\dfrac{v_{0}^2}{2a}-\dfrac{1}{2}(v_{0}t+at^{2}+\dfrac{v_{0}^2}{a}+v_{0}t)\\&=-v_{0}t-\dfrac{1}{2}at^2-\dfrac{v_{0}^2}{a}}$

なんだか見知らぬ式になりました．やはり，$x=v_{0}t+\dfrac{1}{2}at^2$は移動距離の式ではないようですね．それでは，座標$x$の計算をしてみましょう．O-M-Nは青の面積だけ$+x$方向に進んで，MNは緑の面積だけ$-x$だけ進むので

$x=$(青の面積)-(緑の面積)$

です．したがって

$\eqalign{x&= \dfrac{1}{2}v_{0}t_{0}-\dfrac{1}{2}(t-t_{0})|v_{0}+at| \\&= \dfrac{1}{2}v_{0}(-\dfrac{v_{0}}{a})-\dfrac{1}{2}(t-(-\dfrac{v_{0}}{a}))(-v_{0}-at)\\&= -\dfrac{v_{0}^2}{2a}+\dfrac{1}{2}(t+\dfrac{v_{0}}{a})(v_{0}+at)\\&= -\dfrac{v_{0}^2}{2a}+\dfrac{1}{2}(v_{0}t+at^{2}+\dfrac{v_{0}^2}{a}+v_{0}t)\\&= v_{0}t+\dfrac{1}{2}at^2}$

やはりこちらは$x=v_{0}t+\dfrac{1}{2}at^2$の式と一致しました．

　まとめ

等加速度運動の式，$x=v_{0}t+\dfrac{1}{2}at^2$の式の$x$は移動距離ではなく，座標（$t=0$にあった場所からの変位）です．特に折り返しの運動のときは十分注意をして問題を解いてください．