
導体棒は磁場中を運動すると電池になるんだよね.

はい.導体棒が電池となります.
あらためてまとめておきましょう.
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は,PQの長さを$l$,PQ方向に垂直な速さを$v_{\perp}$,導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば,
$V=v_{\perp}Bl$
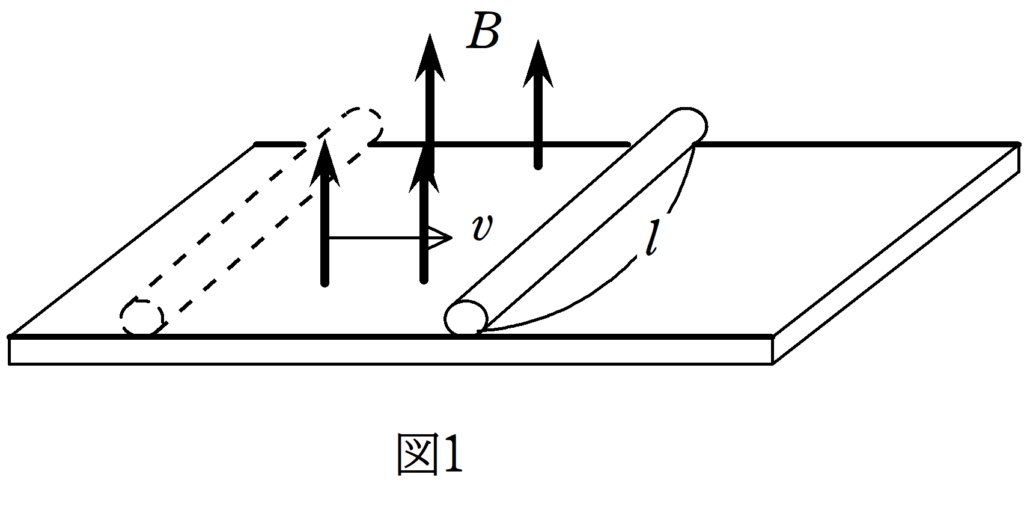
磁場中を導体棒が動く→起電力が生じる

導体棒が電池になる理由は下記の記事で扱っています.

ここで疑問なんだけど,導体棒の磁場中の運動では,電磁力がした仕事や誘導起電力がした仕事をかかないのはなぜなんだろう??

たとえば,下図のように,外力を加えて導体棒を等速度運動させるでしょ.
すると,回路に電流が流れて電磁力を受けるから,エネルギー収支の式は
(外力がした仕事)+(電磁力がした仕事)+(誘導起電力がした仕事)=(ジュール熱)
になると思うんだけど,なぜか,どの問題集をみても
(外力がした仕事)=(ジュール熱)
になっているんだ.

そうですね.それは
(電磁力がした仕事)+(誘導起電力がした仕事)=0
になるからなんです.

え!?
そうだったの??

はい.
それでは,順に考えていきましょう.
図2のように,抵抗$R$をつないで,回路をつくってみましょう.
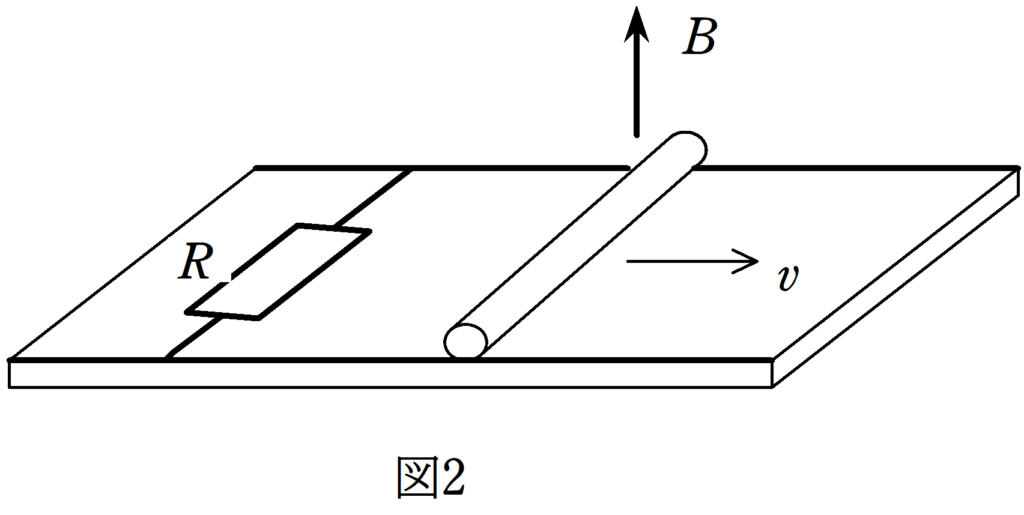

すると,導体棒が電池となり,導体棒と抵抗に電流が流れます.図3をみてください.
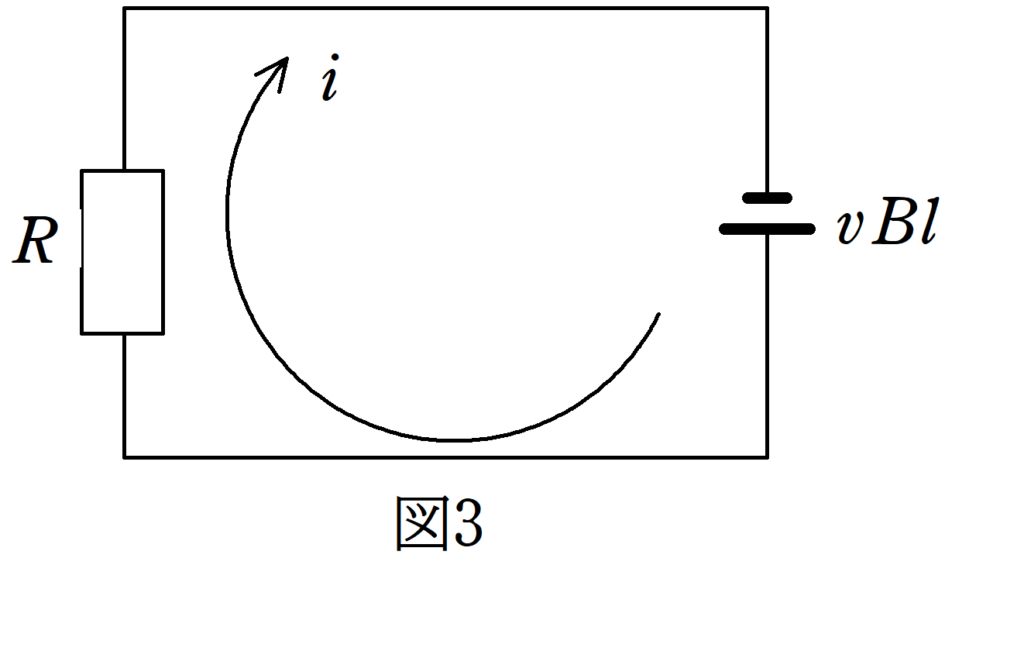

オームの法則より,回路に流れる電流$i$は
$i=\dfrac{vBl}{R}$
になるね.

そうですね.
すると,磁場中に電流が流れるわけですから,導体棒は電磁力を受けます.
磁束密度$B$内に磁場と垂直な方向に電流$I$が流れるとき,長さ$l$分の電流が受ける力$F$は
$F=IBl$
となります.
つまり,今回の場合,フレミング左手の法則も考慮して大きさ
$F=iBl=\dfrac{v(Bl)^2}{R}$
の電磁力が図4のように左方向にはたらきます.
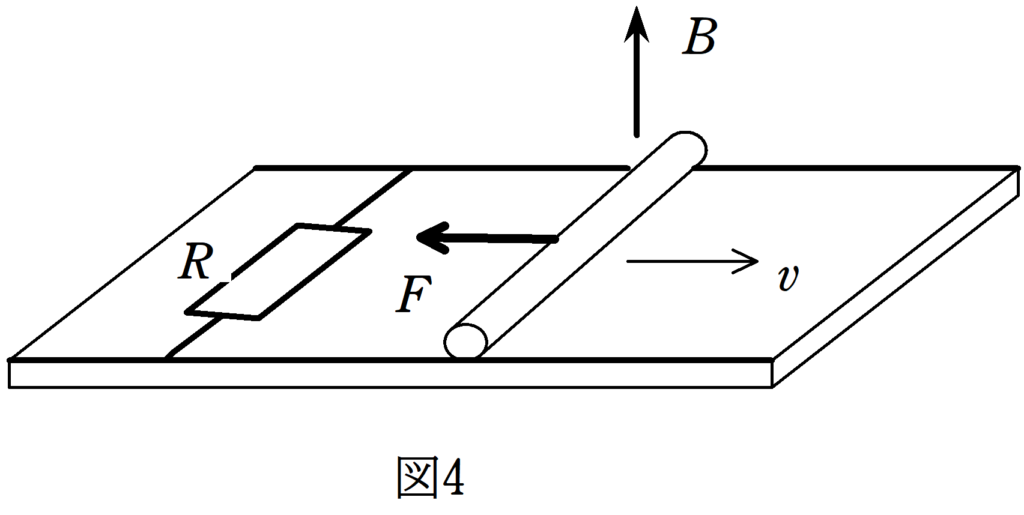

そうすると,導体棒は負の仕事を受けて減速し,やがて静止することになるね.

さて,本題にはいります.
そもそも電磁力はローレンツ力と同じはずです.
しかしローレンツ力は仕事をしません.
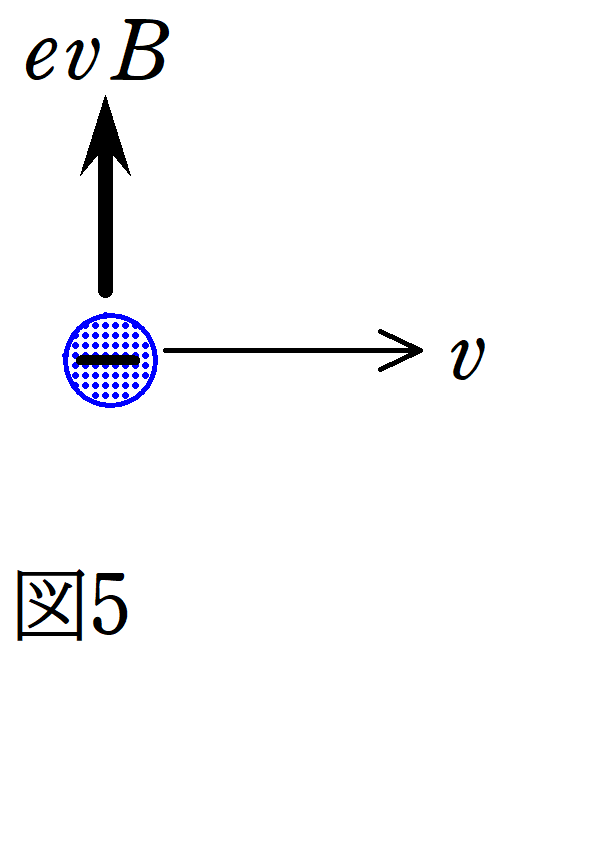

そういえば!
ローレンツ力は常に速度の方向と垂直に力がはたらくんだったね.
ちなみに,ローレンツ力は次のようにはたらく力だったね.
磁場の大きさを$B$,磁場に垂直な速度の大きさを$v$,荷電粒子の電荷を$q$のとき,荷電粒子が受けるローレンツ力の大きさ$f$は
$f=|q|vB$
向きはフレミング左手の法則に従う.
$\clubsuit$フレミング左手の法則$\clubsuit$
親指→ローレンツ力の向き
人差し指→磁場の向き
中指→電流の向き(正電荷の動く向き,負電荷の動く向きと逆)

電磁力とローレンツ力は同じで,ローレンツ力は仕事をしない...
じゃあ,電磁力がする負の仕事はなんなんだ??
つじつまが合わない.
なんで,導体棒にはたらく電磁力の仕事は0じゃないんだろう?

実は,ちゃんとローレンツ力がした仕事は0になっているんです.
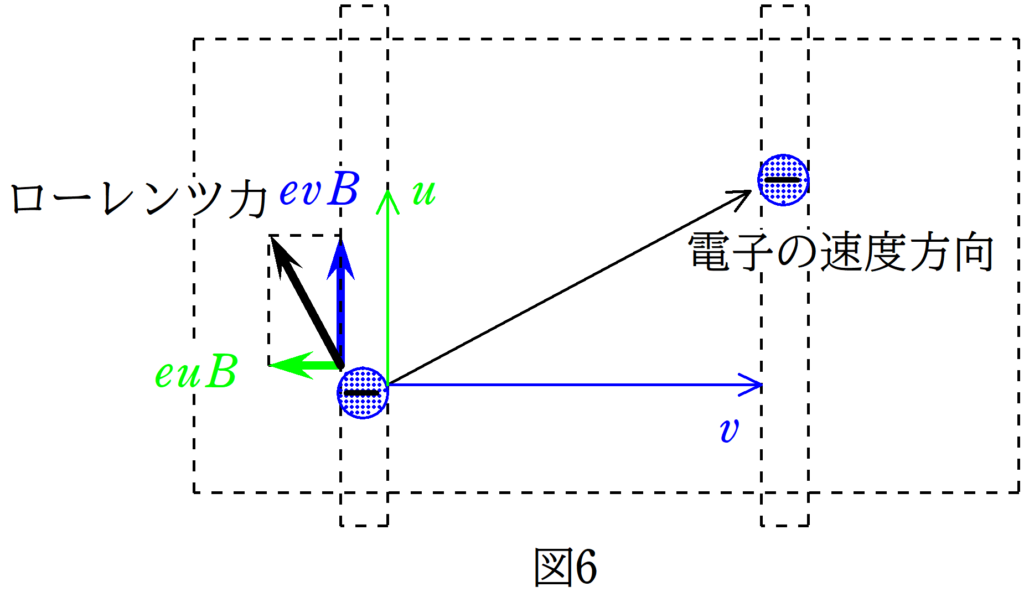

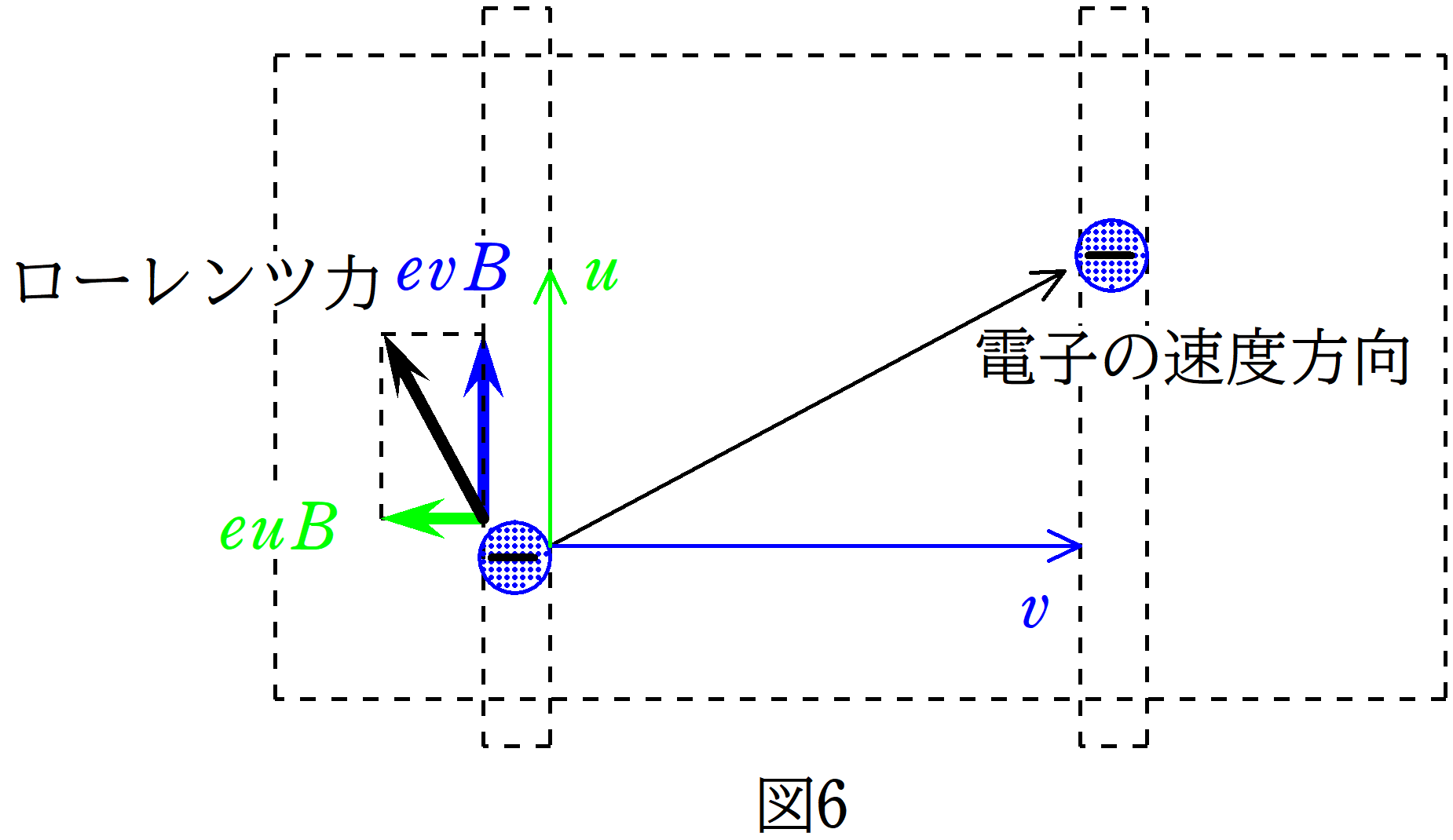
導体棒が右方向に速さ$v$で動いているときに,導体棒には電流が流れているため,静止している人からみると,自由電子は図6の方向に速度をもっているはずです.
つまり
青の速度$v$と緑の速度$u$
です.
すると,それぞれの速度成分がローレンツ力をうけます.
$v$の成分のローレンツ力が導体棒の長さ方向に大きさ$evB$,$u$の成分のローレンツ力が図6の左方向に大きさ$euB$です.
$evB$の力の成分は誘電起電力もたらします.
そして,$euB$の成分がいわゆる電磁力とよばれているものとなります.
このように,ローレンツ力は2つの速度成分を分解すると,それぞれ
誘導起電力と電磁力
に分けることができるのです.
そして,ローレンツ力がする仕事が0であることから次のことが言えます.
(電磁力がした仕事)$+$(誘導起電力がする仕事)$=0$ $\dots (\ast)$

なるほど!
そういうことだったのか!
でも,本当にそうなっているのかな?

では,計算してみましょう.
導体棒の長さを$l$,断面積を$S$,単位体積当たりの自由電子の数を$n$とすると,この導体棒全体にはたらく電磁力は,$I=euSn$の関係の関係も考慮して(正確には電子にはたらくローレンツ力の和が電磁力というわけではなく,静止している正の電荷が受ける静電気力の和が静電気力になるが,大きさ向きは同じになる.)
$euB\cdot Sln = IBl$
速さが$v$であることと,電磁力が負の仕事をしていることから,単位時間当たりに電磁力がする仕事$P_{1}$は
$P_{1}=-IBl\cdot v$ $\dots (2\ast)$
一方,ローレンツ力$evB$がはたらいているときの誘導起電力の大きさ$V$は
$V=vBl$
あるから,この誘導起電力がする単位時間あたりにする仕事$P_{2}$は
$P_{2}=VI=vBl\cdot I$ $\dots (3\ast)$
$(2\ast)$,$(3\ast)$より,$ (\ast)$が成り立つことが確認できますね.

本当になってる!
では,まとめておきましょう.
導体棒と回路のエネルギー収支の式を立てるとき,
(電磁力がする仕事)+(誘導起電力がする仕事)=0
なので,エネルギー収支の式に入れなくてもよい.

演習問題を解くときは注意をしよう!

コメント
[…] […]
[…] […]
[…] […]
[…] [磁場中の導体棒の運動]電磁力がする仕事は0??NEKO導体棒は磁場中を運動… […]
[…] なぜ,電磁力がした仕事を式に入れないのか? […]
[…] なぜ,電磁力がした仕事を式に入れないのか?NEKO導体棒は磁場中を運動す… […]