
今回は磁場中で静止している導体棒に電池をつないで,運動させる問題です.
前回までが,力を加えて導体棒を動かし,電流を発生させていました.
発電機:力学的エネルギー→電気エネルギー
モーター:電気エネルギー→力学的エネルギー
のイメージを持っておいてください.
前回の内容です.

発電機の問題は途中経過がわかっていないと,最終的に導体棒がどのような運動をするのかを理解できません.
解説で導体棒の運動の途中経過の解説もしてあります.

今回も次のことを確認しておこう!
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は,PQの長さを$l$,PQ方向に垂直な速さを$v_{\perp}$,導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば,
$V=v_{\perp}Bl$
- 回路の式(オームの法則,コンデンサーの基本式,電荷保存則など)
- 導体棒の運動に関する式(つり合いの式,運動方程式,運動量保存則など)
- 導体棒と回路の系全体のエネルギー収支の式
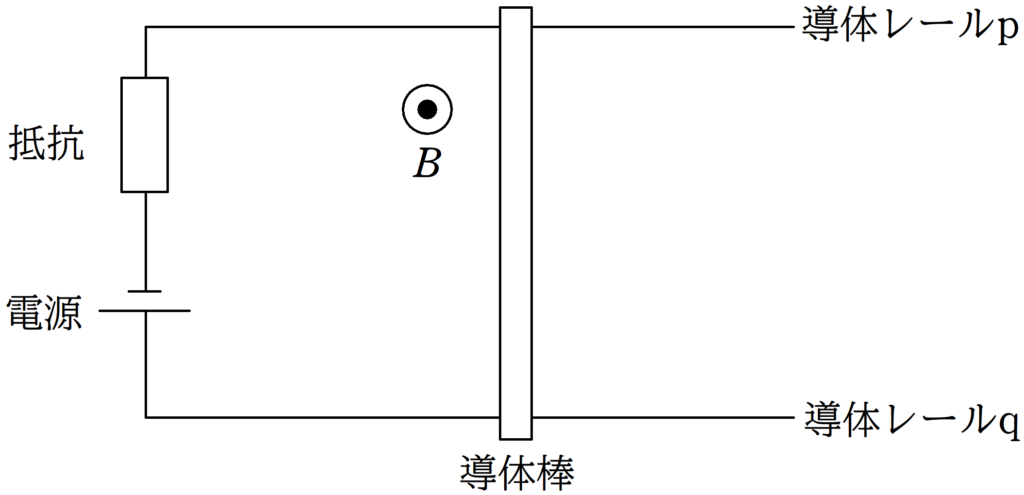
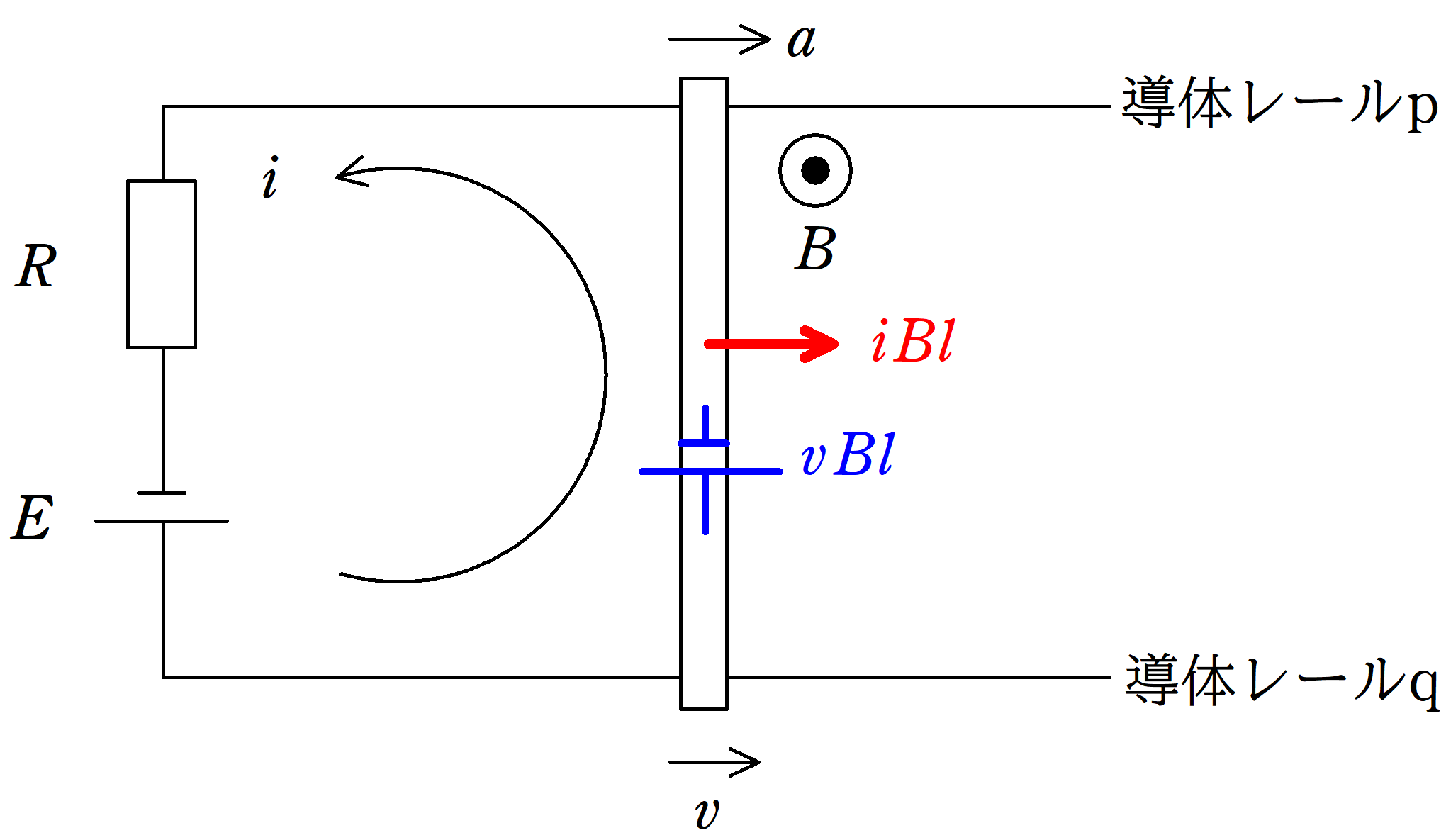
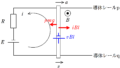
内部抵抗の無視できる起電力$E$の電池,平行に設置された導体レールp , q,電気抵抗$R$の抵抗を図のようにつなげた.また,画面奥から手前方向に一様な磁場をかけ,その磁束密度の大きさを$B$とする.
2つの導体レールに垂直に交わるように,長さ$l$,質量$m$の導体棒を静かにおいたところ,導体棒は運動をはじめた.導体棒と導体レールの間の摩擦は無視できるものとして,次の問いに答えよ.
(1) 導体棒を導体レールにおいた直後に導体棒に流れる電流の大きさを求めよ.また,このとき
の導体棒にはたらく電磁力の大きさを求めよ.
(2) 導体棒を導体レールにおいてから十分時間が経ったときの導体棒に流れる電流の大きさを求めよ.また,このときの導体棒の速さを求めよ.
<解答>
(1)
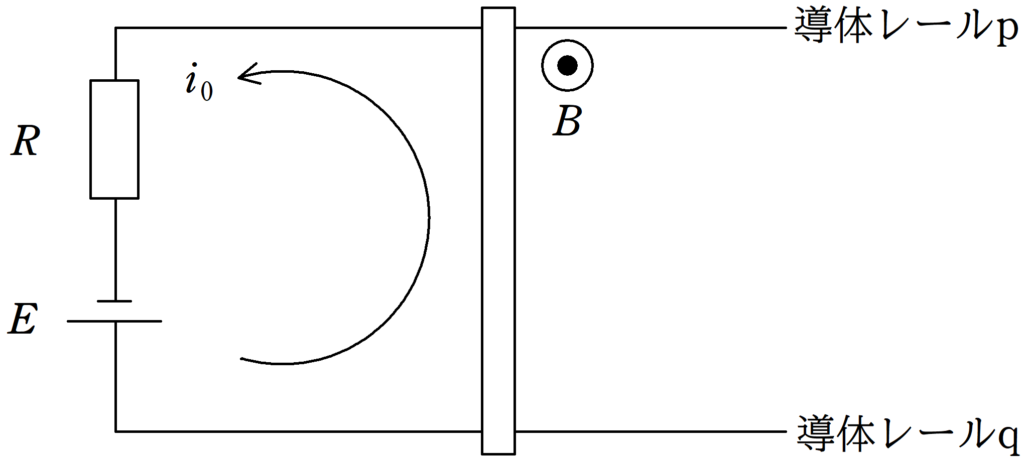

まずは,「1.回路の式」を立ててみましょう.
導体棒はまだ動いていないので,誘導起電力は生じていません.
回路に流れる電流を図のように$i_{0}$とすると,キルヒホッフの法則より
$E=Ri_{0}$ $\therefore$ $i_{0}=\dfrac{E}{R}$
電流が磁場中を流れているので,電磁力を受けます.電磁力の大きさ$F_{0}$は
$F_{0}=i_{0}Bl=\dfrac{EBl}{R}$
(2)

(2)の答えの前に,(1)と(2)の間の導体棒の運動について考えてみましょう.
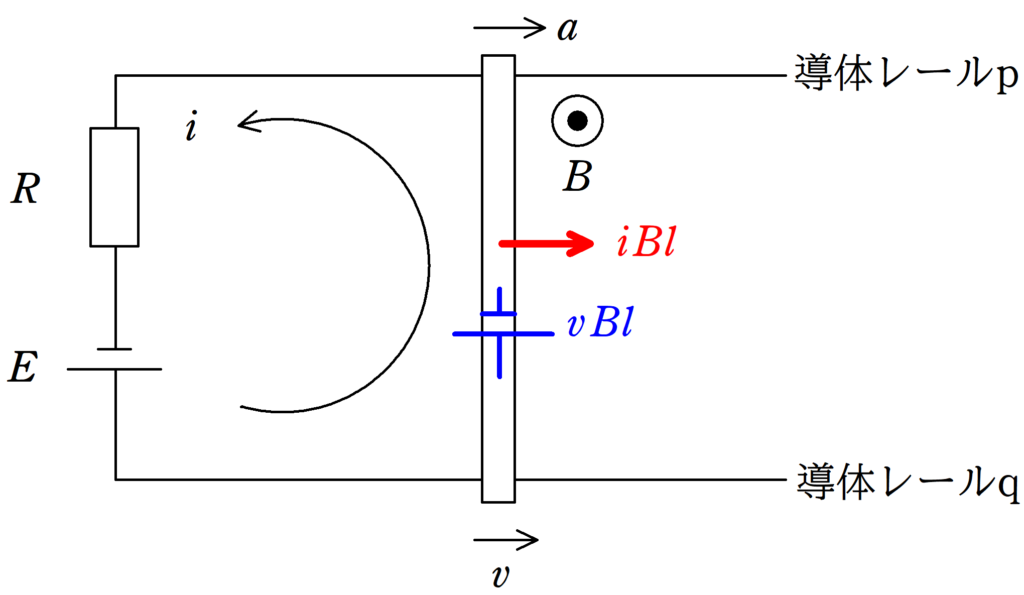

設定はこうです.
導体棒が動き始めたときの時刻を$t=0$として,時刻$t$の導体棒の速度を$v$,加速度を$a$,流れる電流を$i$と設定します.向きは上図のようにしましょう.
では,このとき
1.回路の式
2.導体棒の運動方程式
はどのようになるでしょうか?

回路の式は
$E-vBl-Ri=0$ $\dots (\ast)$
運動方程式は
$ma=iBl$ $\dots (2\ast)$
かな.

正解です.
また,加速度は
$a=\dfrac{\Delta v}{\Delta t}$
と表すことができるので,$(2\ast)$に代入すると,次のようになります.
$m\dfrac{\Delta v}{\Delta t}=iBl$
$\therefore i=\dfrac{m}{Bl}\dfrac{\Delta v}{\Delta t}$ $\dots (3\ast)$
$(3\ast)$を$(\ast)$に代入して$i$を消去しましょう.

$E-vBl-\dfrac{mR}{Bl}\dfrac{\Delta v}{\Delta t}=0$
だから
$\dfrac{mR}{Bl}\dfrac{\Delta v}{\Delta t}=E-vBl$ $\dots (4\ast)$
だね.

では,$(4\ast)$をもとに,縦軸が速度$v$,横軸が時間$t$のグラフをかいてみましょう.

力学でよく出てくる$v-t$グラフだね.
$v-t$グラフの傾きは$a=\dfrac{\Delta v}{\Delta t}$だったね.
$(4\ast)$を加速度がわかりやすいように変形すると
$\dfrac{\Delta v}{\Delta t}=\dfrac{Bl}{mR}(E-vBl)$
導体棒は$t=0$で静止してたんだから加速度は$\dfrac{BlE}{mR}$だね.
そして,導体棒がどんどん加速していくと,$E-vBl$の部分が小さくなるから,加速度がだんだんと小さくなるんだね.

そういうことです.
導体棒が速くなればはやくなるほど加速度が小さくなるので,$v-t$グラフの傾きも小さくなります.
実際にかいてみると,次のようになります.
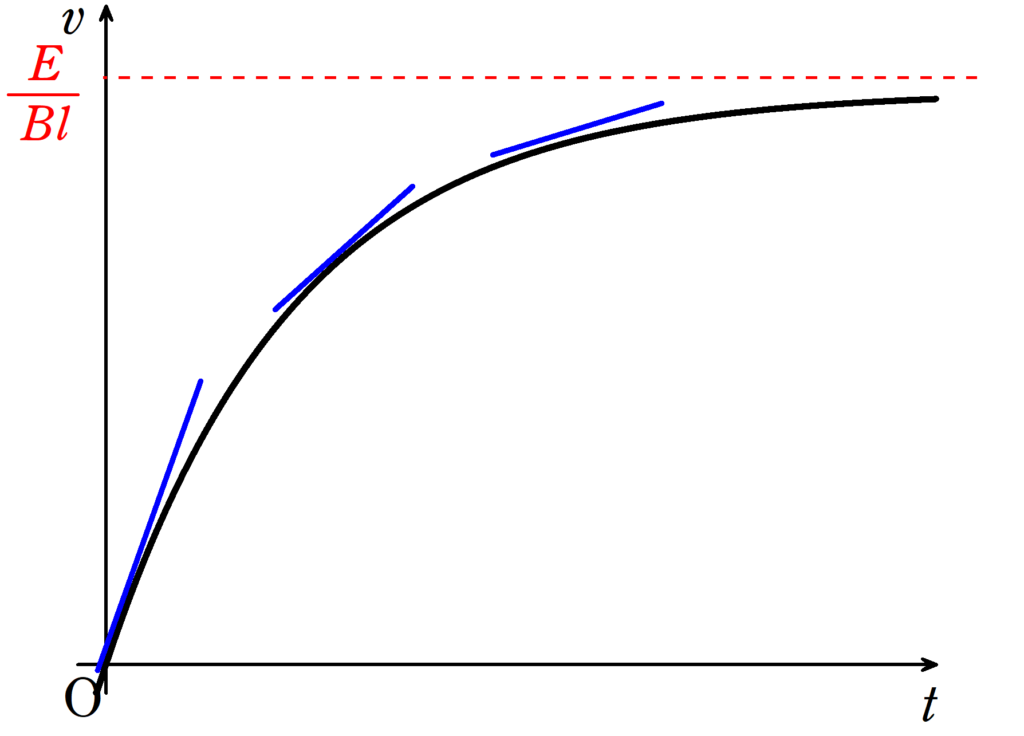

最終的には,$E-vBl=0$となってしまって,傾きが0になるんだね.
つまり,終端速度は$v=\dfrac{E}{Bl}$になるんだ.
ということは,十分時間が経つと,$a=\dfrac{\Delta v}{\Delta t}$は0になるんだから,$(3\ast)$の$i=\dfrac{m}{Bl}\dfrac{\Delta v}{\Delta t}$より,電流は0になるんだね.

そうです.
電流の時間変化のグラフは次のようになります.
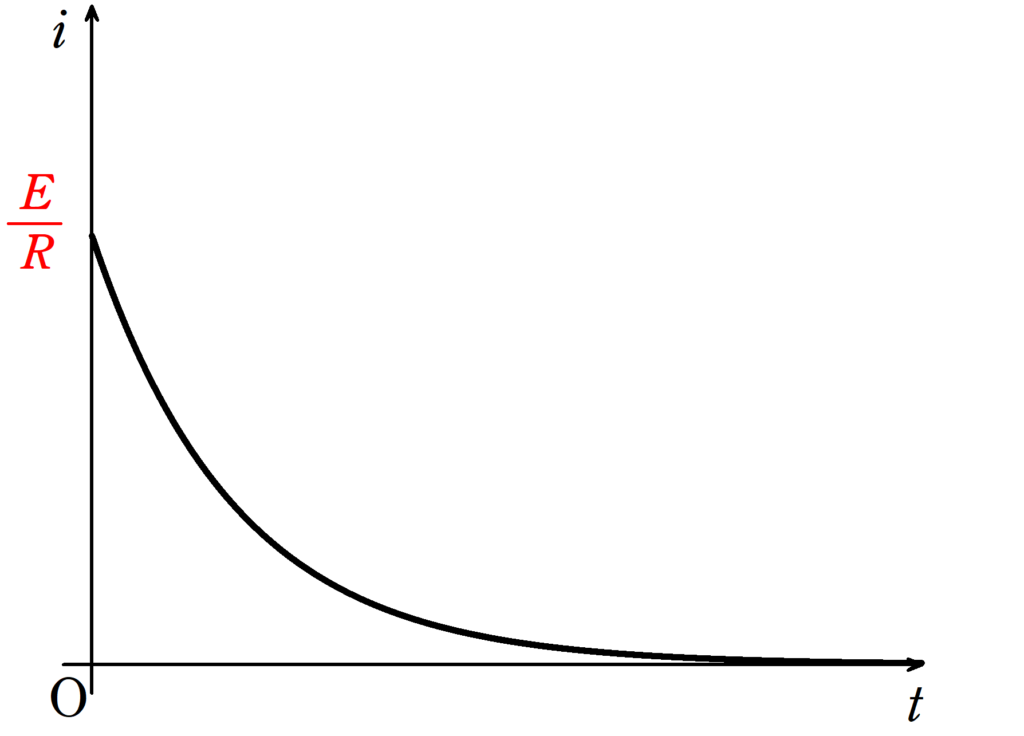

この手の問題は最終的に電流が0になって,一定の速さになるって覚えておけばいいのかな??

それはやめた方がよいです.
最終的な状態は問題によってさまざまです.
問題ごとに式を立てて考えた方がよいでしょう.

なるほど,じゃあ,問題演習を通して,どのような形があるのかを整理していくのが一番の近道かな.
ところで,(2)の答えは,最終的に導体棒に流れる電流は0,導体棒の速さは$\dfrac{E}{Bl}$ということだね.
次回の内容はこちらです.


コメント
[…] […]
[…] […]
[…] […]