
前回から,モーター(電気エネルギー→力学的エネルギー)の問題を扱っています.
今回は摩擦ありの問題です.
摩擦があると,何が変わるのでしょうか??
前回の内容です!
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は,PQの長さを$l$,PQ方向に垂直な速さを$v_{\perp}$,導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば,
$V=v_{\perp}Bl$
- 回路の式(オームの法則,コンデンサーの基本式,電荷保存則など)
- 導体棒の運動に関する式(つり合いの式,運動方程式,運動量保存則など)
- 導体棒と回路の系全体のエネルギー収支の式
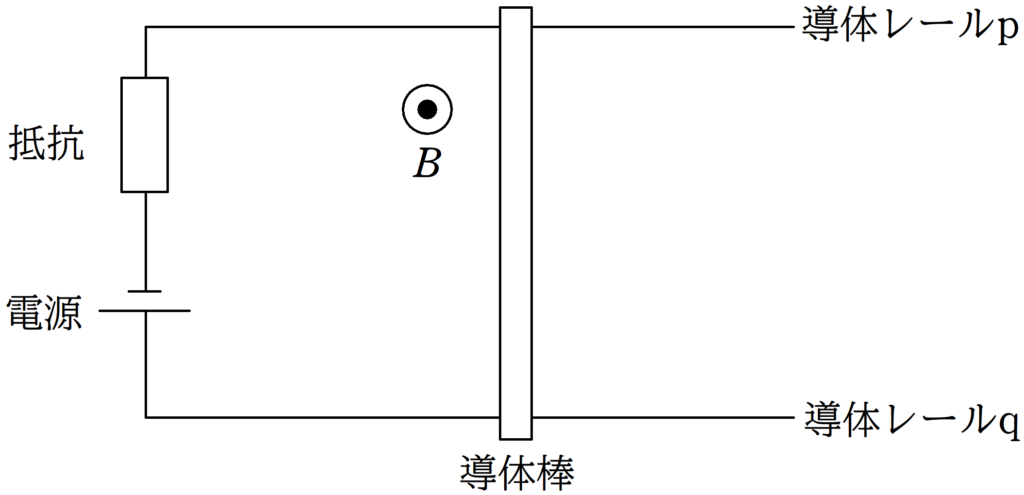
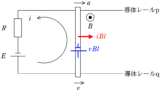
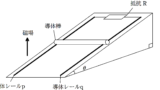
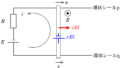
内部抵抗の無視できる起電力$E$の電池,平行に設置された導体レールp , q,電気抵抗$R$の抵抗を図のようにつなげた.また,画面奥から手前方向に一様な磁場をかけ,その磁束密度の大きさを$B$とする.
2つの導体レールに垂直に交わるように,長さ$l$,質量$m$の導体棒を静かにおいたところ,導体棒は運動をはじめた.導体棒と導体レールの間の動摩擦係数を$\mu$として,次の問いに答えよ.
(1) 導体棒を導体レールにおいた直後に導体棒に流れる電流の大きさを求めよ.また,このときの導体棒にはたらく電磁力の大きさを求めよ.
(2) 導体棒を導体レールにおいてから十分時間が経ったときの導体棒に流れる電流の大きさを求めよ.また,このときの導体棒の速さを求めよ.

動摩擦力がはたらく以外はほとんど前回と同じ内容だね.
確か,前回は,十分時間が経つと
導体棒の速さ→一定
電流→0
になったね.今回もこのようになるのかな??
<解答>
(1)
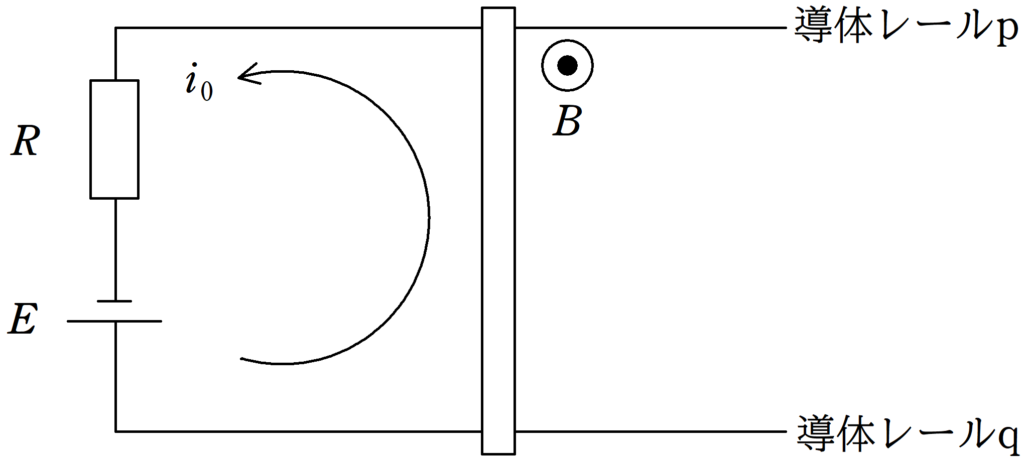
まだ,導体棒が動いていないので,誘導起電力は生じません.
回路に流れる電流を$i_{0}$とすると,キルヒホッフの法則より
$E-Ri_{0}=0$ $\therefore i_{0}=\dfrac{E}{R}$
また,このときの導体棒にはたらく電磁力の大きさ$F_{0}$は
$F_{0}=i_{0}Bl=\dfrac{EBl}{R}$
(2)
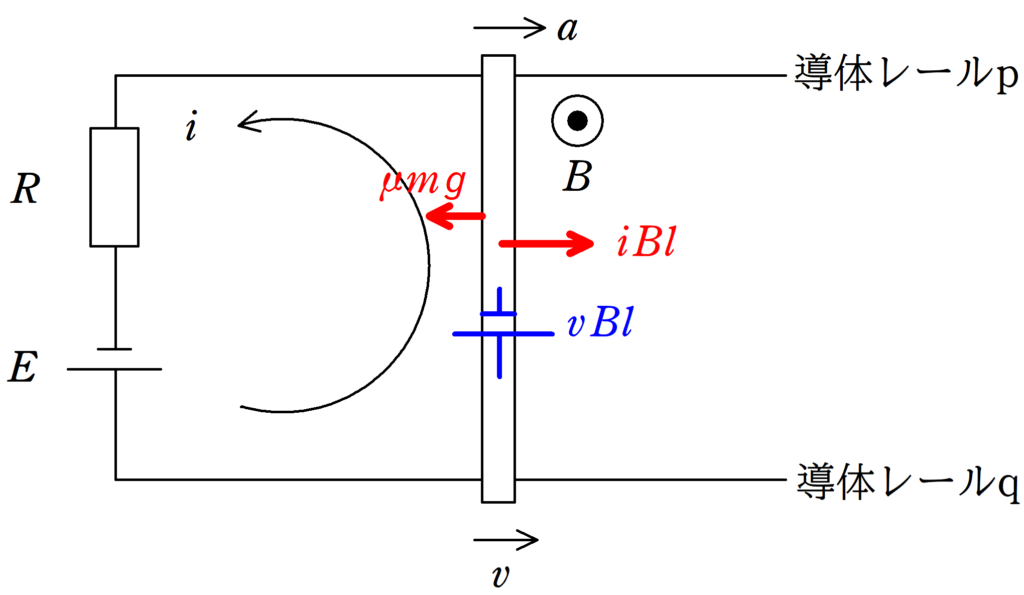

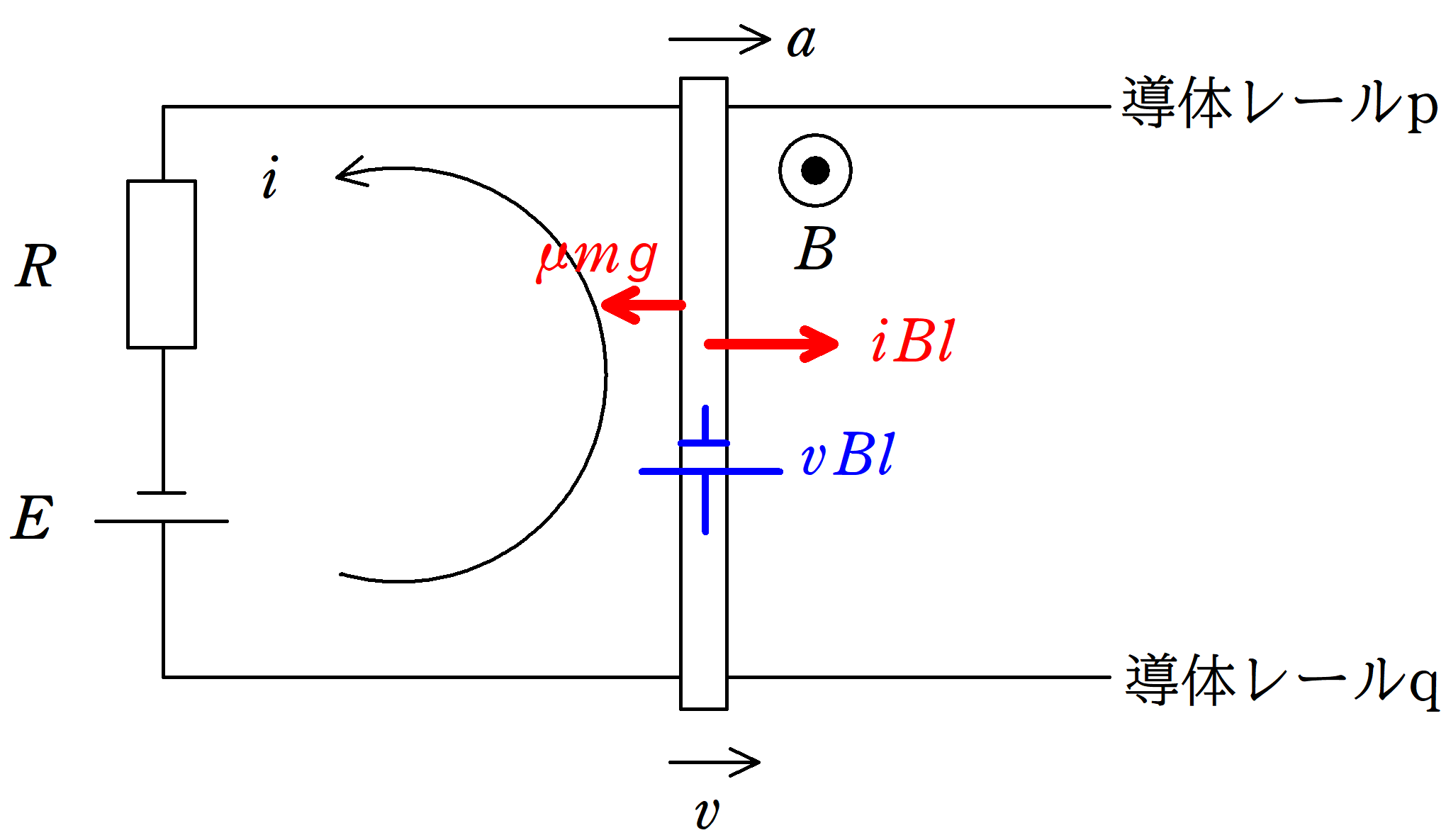
$t=0$で導体棒が動き出したとしましょう!
時刻$t$における,導体棒の速度を$v$,加速度を$a$,回路に流れる電流を$i$とすると,キルヒホッフの法則と導体棒の運動方程式はそれぞれ次のようになります.
キルヒホッフの法則より
$E-vBl-Ri=0$ $\therefore i=\dfrac{E-vBl}{R}$ $\dots (\ast)$
運動方程式より
$ma=iBl-\mu mg$
$(\ast)$を代入して
$\eqalign{ma&=\dfrac{E-vBl}{R}Bl-\mu mg\\&=-\dfrac{B^{2}l^{2}}{R}v+\dfrac{EBl}{R}-\mu mg}$

この運動方程式は前回もやったね.
まとめておこう!
質量を$m$,加速度を$a$,速度を$v$,正の比例定数を$k$,定数を$C$とする.
運動方程式
$ma=-kv+C$
は,十分時間が経つと速度が一定になる.(加速度が0になる.)

上のことは問題を解く目安として覚えておくといいね!
ただ,すべての導体棒の問題が”十分時間が経つと速度が一定になる”わけではないよ.
場合によっては等加速度運動をしたり,単振動したりすることもあるから,運動方程式を立てて確認してね.

さて,運動方程式を確認したら,十分時間が経ったときにどのようなことになるかがわかります.
十分時間が経つと,加速度が0になるので,導体棒がつり合います.
電磁力と動摩擦力のつり合いを考えて
$iBl=\mu mg$ $\therefore$ $i=\dfrac{\mu mg}{Bl}$
また,$(\ast)$の式
$E-vBl-Ri=0$ $\therefore v=\dfrac{E-Ri}{Bl}$
に$i=\dfrac{\mu mg}{Bl}$を代入します.
$\eqalign{v&=\dfrac{1}{Bl}(E-R\cdot \dfrac{\mu mg}{Bl})\\&=\dfrac{EBl-\mu Rmg}{B^{2}l^{2}}}$
したがって,十分時間が経つと,$v=\dfrac{EBl-\mu Rmg}{B^{2}l^{2}}$
になります.

十分時間が経ったら,速度が0になったり,電流が0になるという特殊な場合を覚えてはダメだよ.
途中経過のキルヒホッフの式と運動方程式から
$ma=-kv+C$
が出てきたら,十分時間が経つと$a=0$に近づくんだ!
次回の内容はこちら.


コメント
[…] モーター(摩擦あり) 導体棒の磁場中の運動演習⑦[基本]NEKO前回から,モ… 問題 […]
[…] モーター(摩擦あり) 導体棒の磁場中の運動演習⑦[基本]NEKO前回から,モ… […]
[…] [演習問題]波の式を立てる.$y(0 ,t)$から$y(x , t)$の式へ モーター(摩擦あり) 導体棒の磁場中の運動演習⑦[基本] […]