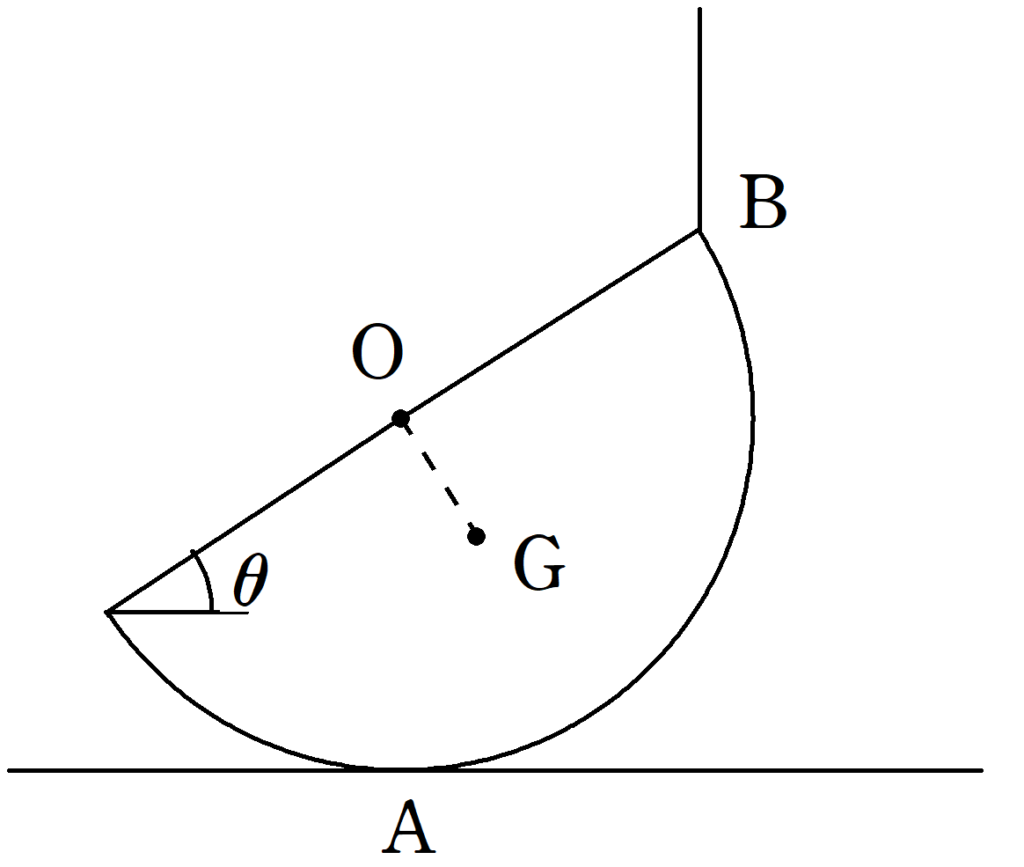
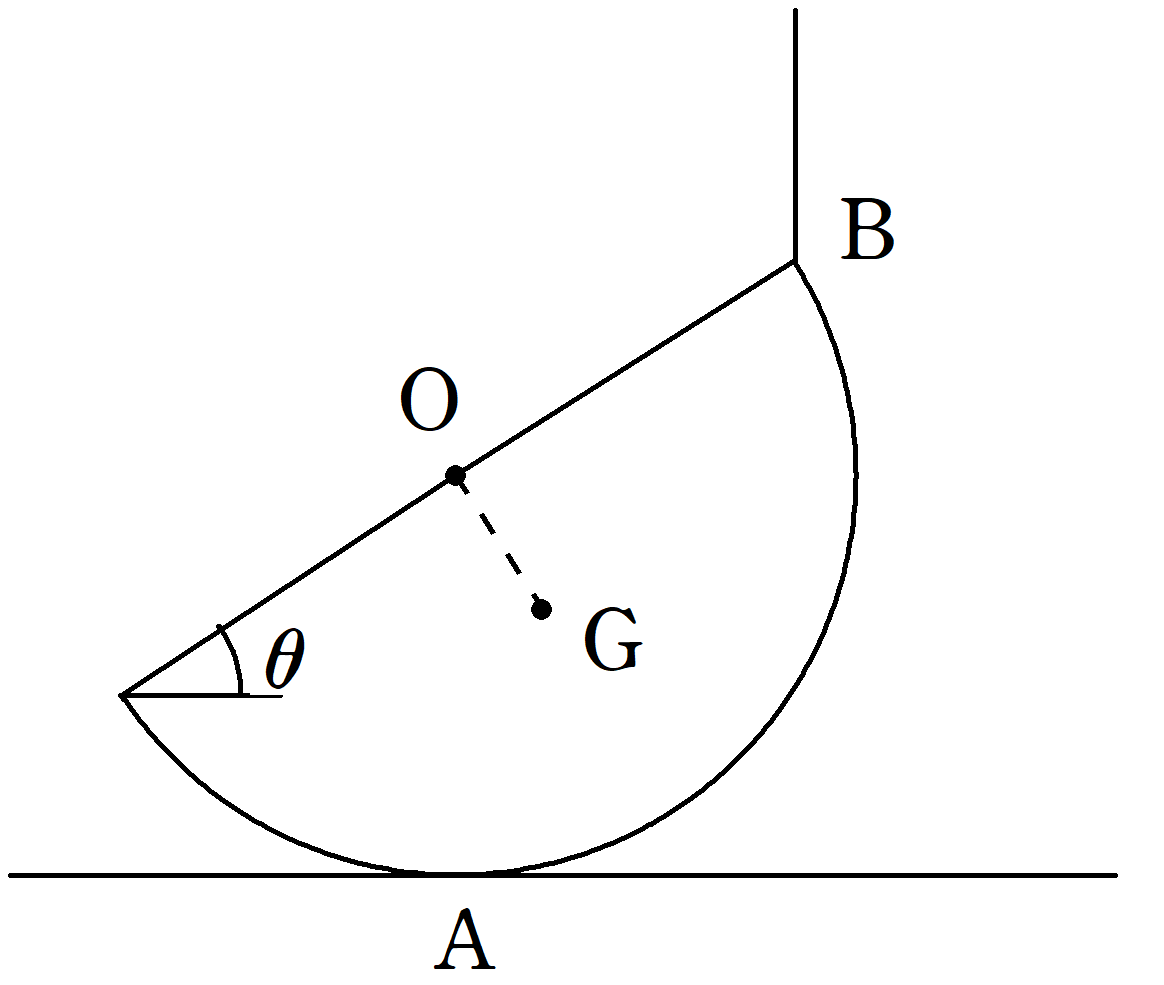
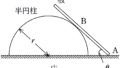
図のように,水平な床の上に,質量$m$の半円柱をおき,$\rm B$に糸を取りつけ力を加える.糸を鉛直に張ると半円柱は$\rm A$で床と接しつり合った.このとき,半円柱の上面は水平面とのなす角$\theta(0<\theta<\dfrac{\pi}{2})$である.半円柱の重心は$\rm G$であり,円柱の底面である半円の半径を$r$とし,半円の中心を$\rm O$とすると,${\rm OG}=a$であった.重力加速度の大きさを$g$として次の問いに答えよ.
(1) 点$\rm A$にはたらく垂直抗力の大きさを$N$,点$\rm B$にはたらく張力の大きさを$T$とする.このとき,半円柱にはたらく鉛直方向の力のつり合いの式を立てよ.
(2) 点$\rm A$まわりの力のモーメントのつり合いの式を立て,張力の大きさ$T$および,(1)より,垂直抗力の大きさ$N$を求めよ.
<解答>
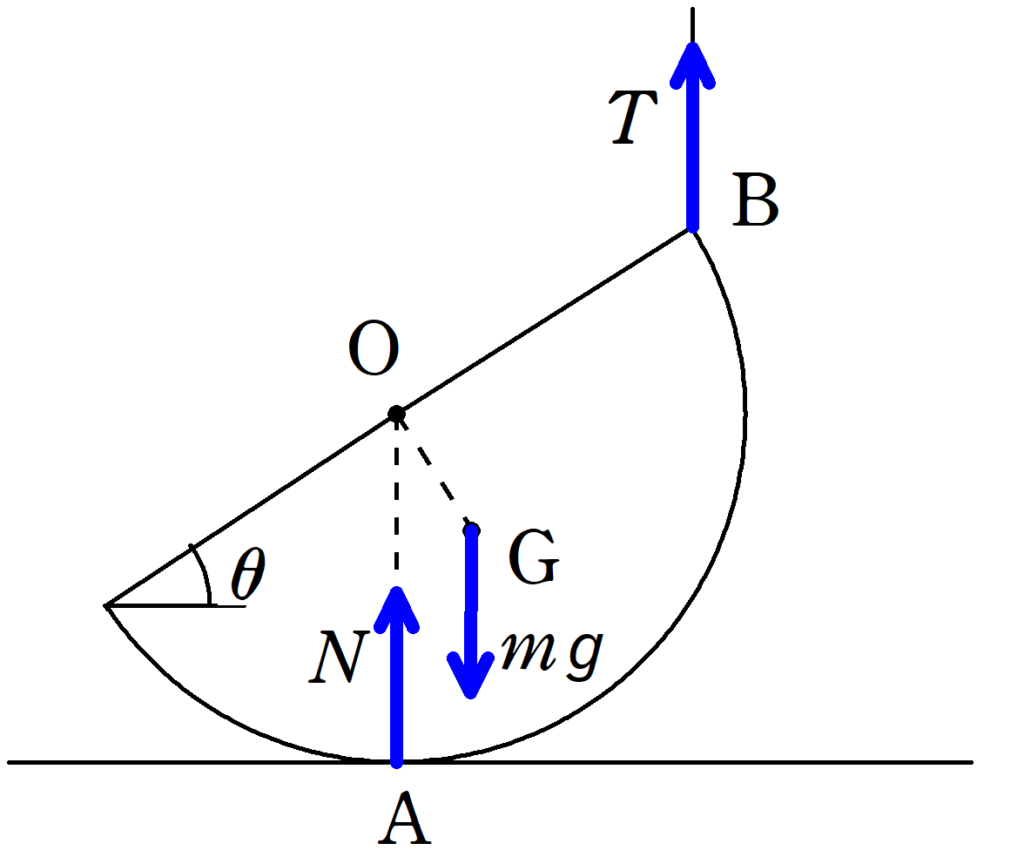

半円柱にはたらく力は上図の3つです.
$\rm A$点に垂直抗力がはたらき,重心$\rm G$に重力が,点$\rm B$には張力がはたらきます.
$\rm A$点の摩擦力は??
と疑問に思うかもしれませんが,水平方向にはたらく力のつり合いを考えれば,摩擦力ははたらかないことがわかります.
★ 鉛直方向のつり合いの式
$T+N=mg$ $\dots (\ast)$ (答)
(2)

次に,点$\rm A$まわりの力のモーメントのつり合いの式を立てます.
ここでは,「作用線平行移動の原理」を使いましょう.
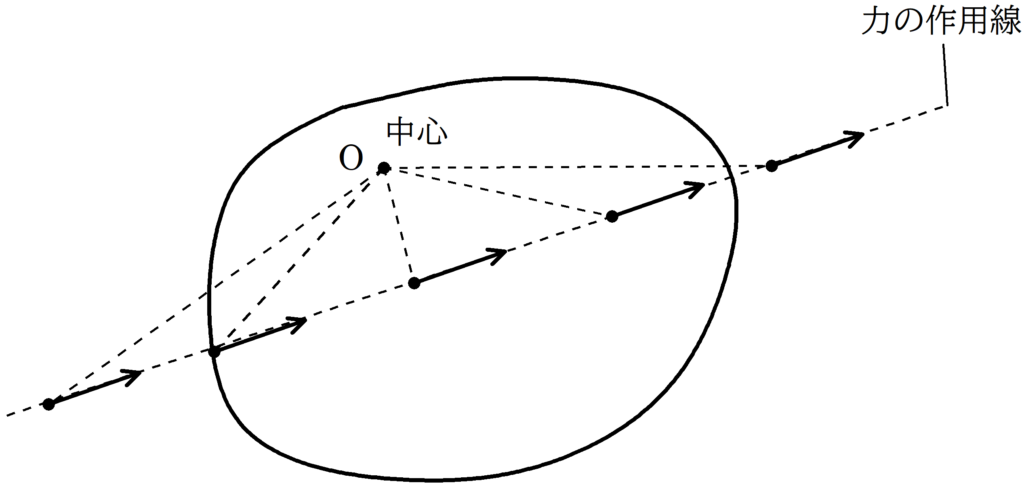
中心を$\rm O$とし,ある始点にはたらく力のモーメントを計算するとき,力の作用線上のどこに移動させても力のモーメントは同じである.
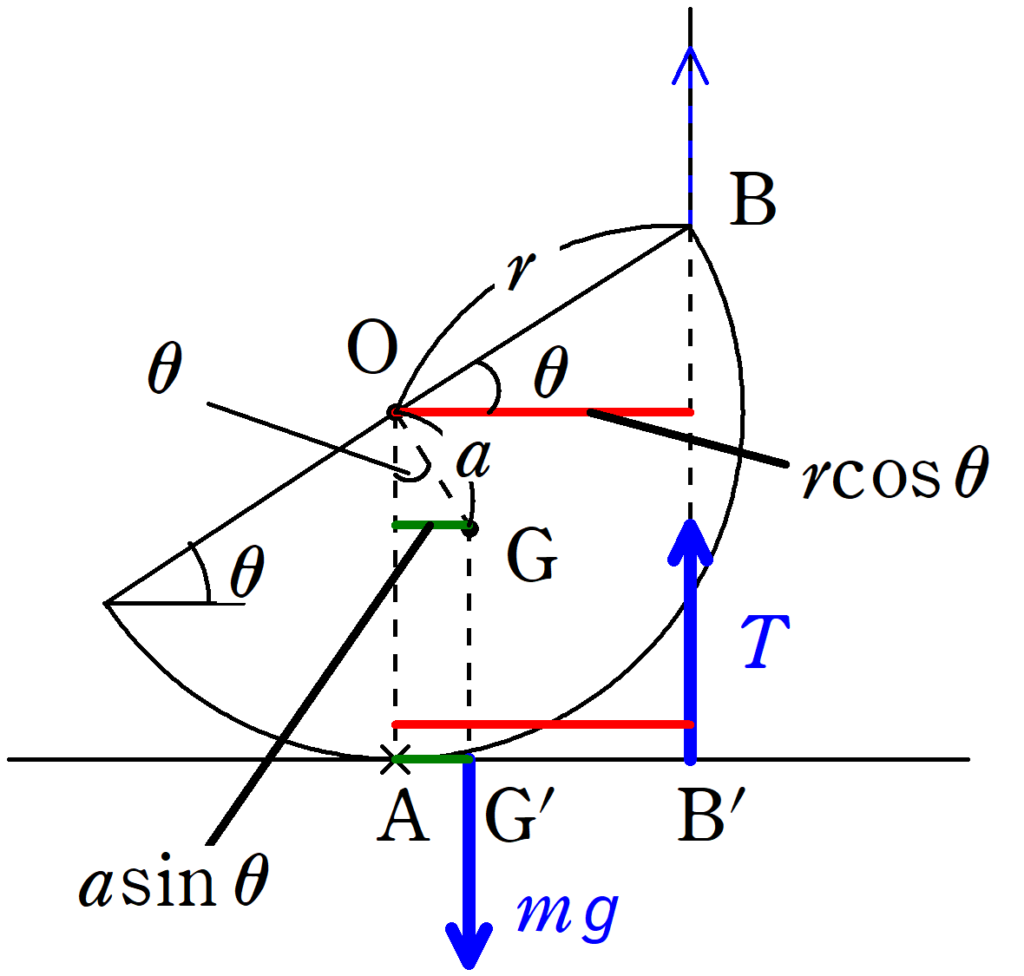

点$\rm A$から重力の作用線,張力の作用線に垂線を下し,その交点を$\rm G^{\prime}$,$\rm B^{\prime}$とし,$\rm G^{\prime}$,$\rm B^{\prime}$まで,力の始点を移動させます.
${\rm AG^{\prime}}=a\sin\theta$(緑線),${\rm AB^{\prime}}=r\cos\theta$(赤線)も確認できます.
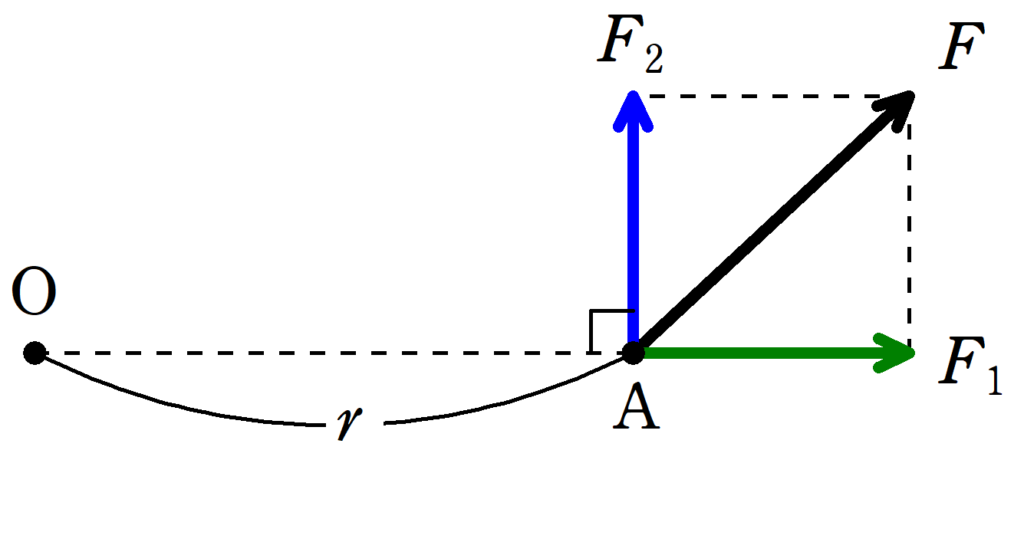
中心$\rm O$から距離$r$の点$\rm A$を始点とした大きさ$F$の力がはたらいている.この力の$\rm OA$方向の成分を$F_{1}$,$\rm OA$に垂直な成分を$F_{2}$とすると,力$F$の点$\rm O$まわりの力のモーメントの大きさ$N$は
$N=rF_{2}$
★ $\rm A$まわりの半円柱に関する力のモーメントのつり合いの式
$a\sin\theta\cdot mg=r\cos\theta\cdot T$
$\therefore T=\dfrac{a\tan\theta}{r}mg$ (答)
$(\ast)$より
$\eqalign{N&=mg-T\\&=mg-\dfrac{a\tan\theta}{r}mg\\&=\left(1-\dfrac{a\tan\theta}{r}\right)mg}$ (答)

コメント