
力のモーメントの問題を解くとき,”作用線平行移動の原理“を使うことがあるよね?
そのとき,物体の外まで作用線を平行移動できるっていうのに違和感があるんだよね.

そうですね.
対象物体にはたらく力について考えているのにも関わらず,物体の外に力がはたらいているように見えて,はじめは違和感を感じるかと思います.
しかし,実は作用線平行移動の原理は,対象物体は関係なく成り立つものであることを示すことができるです.
今日はこの話をしましょう.
作用線平行移動の原理とは

まずは,作用線平行移動の原理についてまとめましょう.
中心を$\rm O$とし,ある始点にはたらく力のモーメントを計算するとき,力の作用線上のどこに移動させても力のモーメントは同じである.
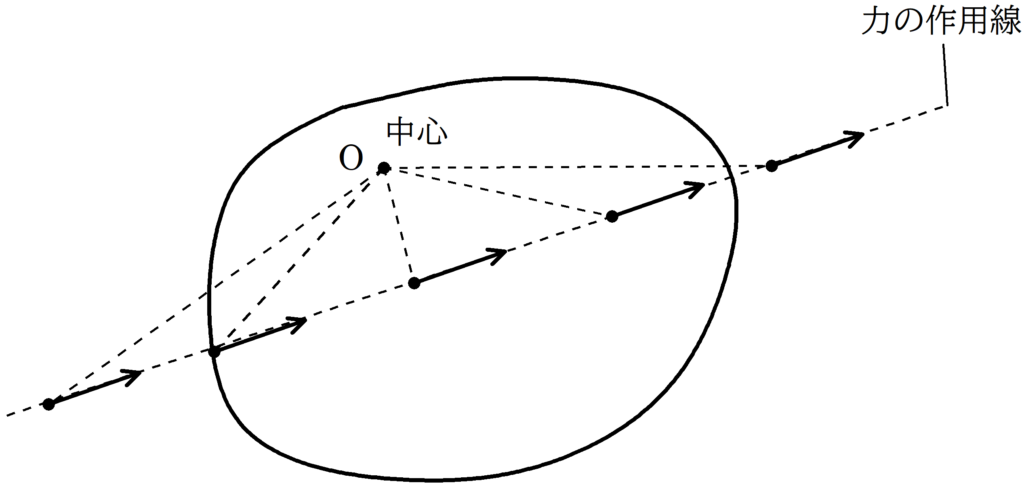

作用線平行移動の原理はやたらと敬遠する人が多いのですが,便利なので,使えるようにしておいたほうがよいでしょう.
作用線平行移動の原理の使い方

でも,”どこにでも動かしていいよ!”ってなると,じゃあどこに動かせばいいんだろう??ってなるんだよね.

そうですね.
実際,試験で使うのは,限られています.
次のことだけ覚えておけばよいでしょう.
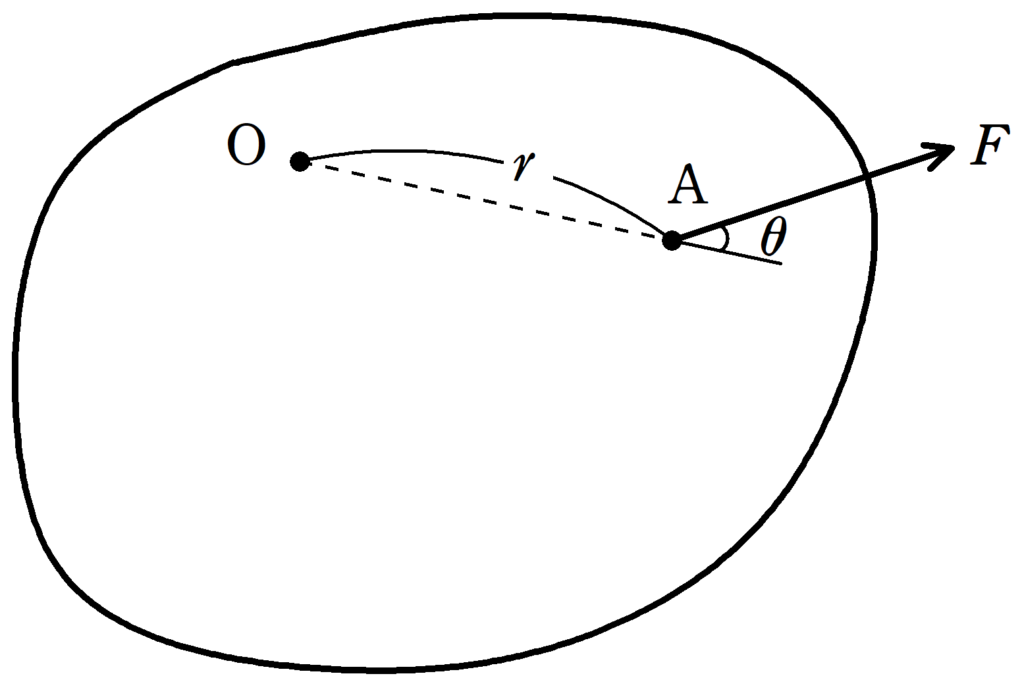

中心を$\rm O$とします.始点$\rm A$に大きさ$F$の力が図の向きにはたらいています.
このくらいの問題だと,そのまま力のモーメントの計算をしてもよいのですが,次のように考えることもできます.
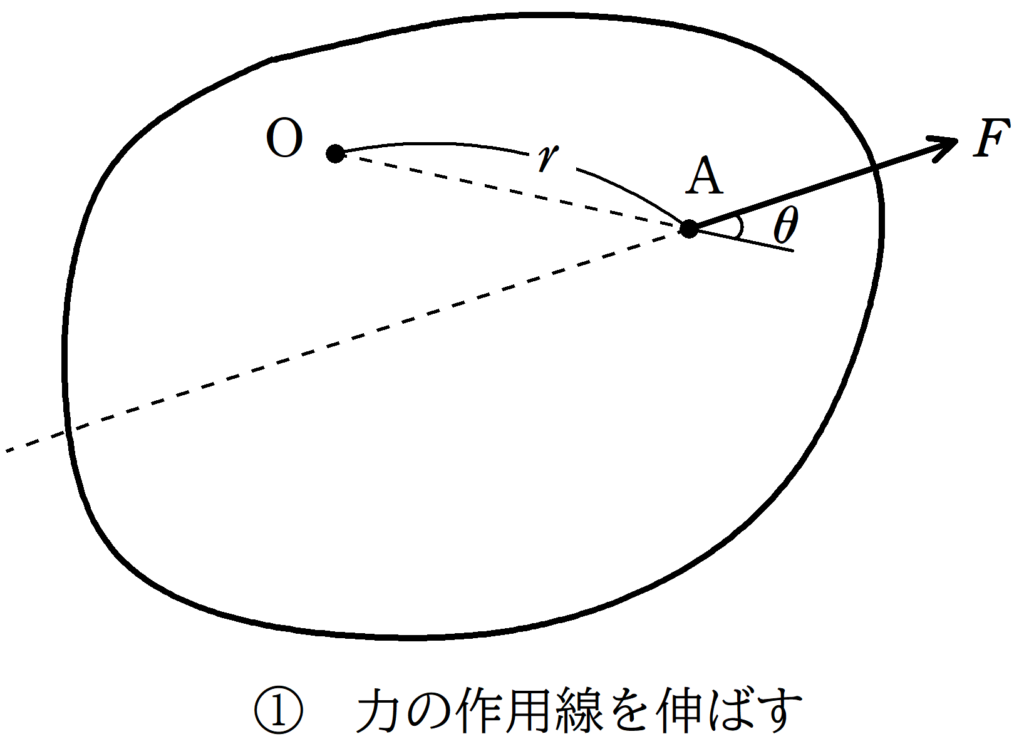
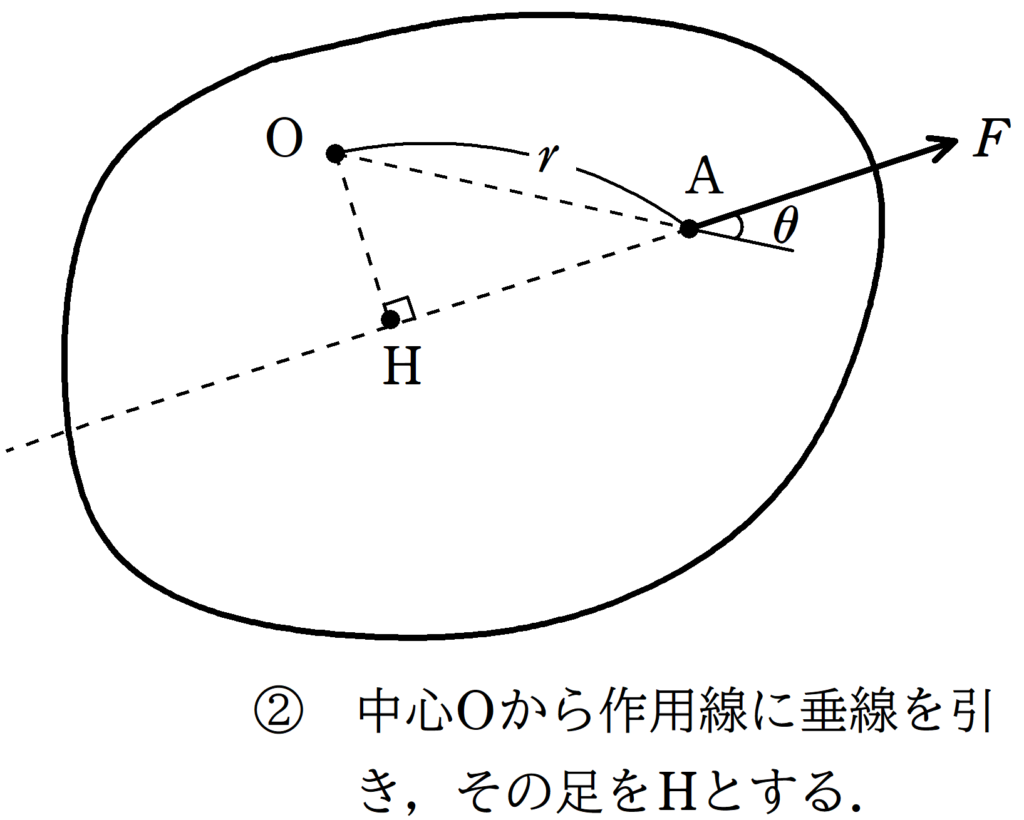
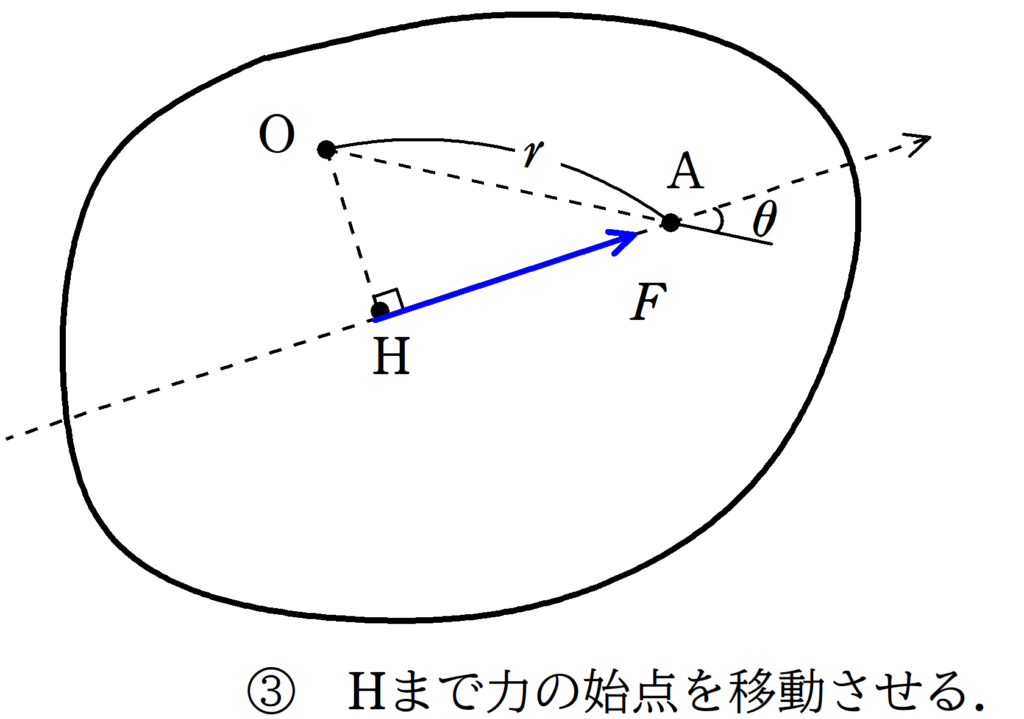

これならできそうかな.
でも,こんなことして,本当に力のモーメントは変化しないのかな?

では,確認してみましょう.
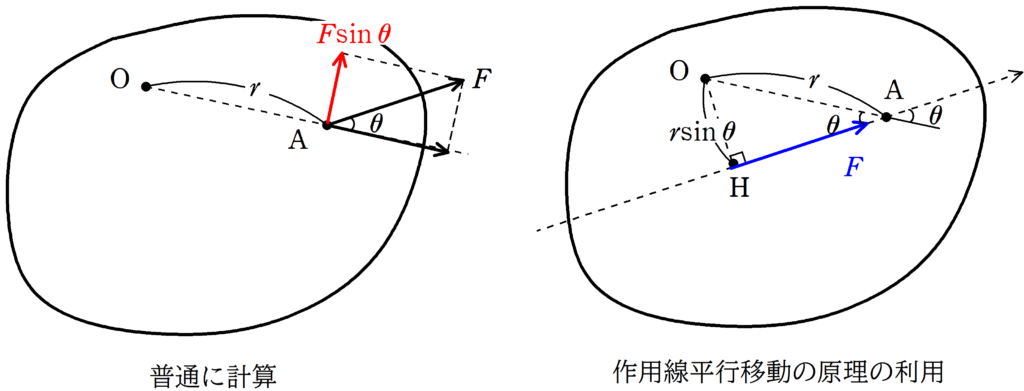
★ 普通に計算
図において,力$F$を$\rm OA$方向と$\rm OA$に垂直な方向に分解すると,$\rm OA$に垂直な方向の力は$F\sin\theta$.
したがって,力のモーメントの大きさ$N_{1}$は
$N_{1}=r\cdot F\sin\theta$
★ 作用線平行移動の原理の利用
図において,$\bigtriangleup \rm OAH$の三角比を考えれば${\rm OH}=r\sin\theta$.
したがって,力のモーメントの大きさ$N_{2}$は
$N_{2}=r\sin\theta \cdot F$

たしかに,$N_{1}=N_{2}$で力のモーメントの大きさは同じだね.
あと,向きについても$\rm O$について反時計回りで変化していないね.
もう少し一般的な作用線平行移動の原理の証明

最後に,より一般的な作用線平行移動の原理の証明をしておきましょう.
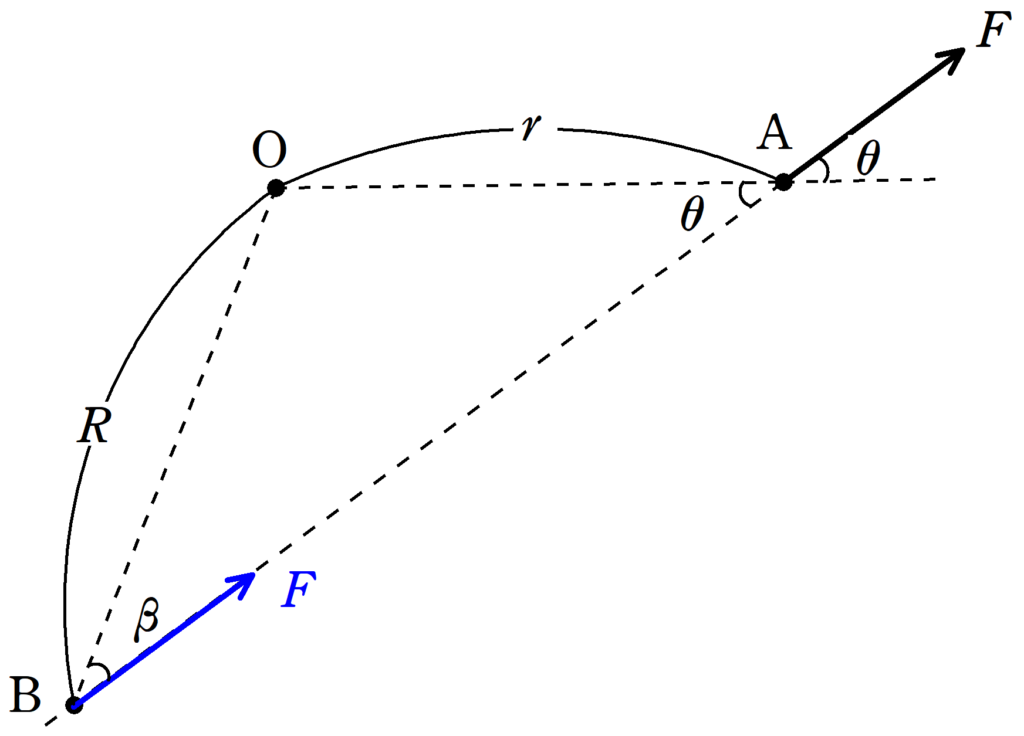

もともと,始点$\rm A$にはたらく力を作用線上の、$\rm B$まで平行移動させてみます.
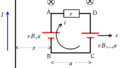
上図のように,力の大きさを$F$,${\rm OA}=r$,${\rm OB}=R$,$\rm \angle OAB=\theta$,$\rm \angle OBA=\beta$とします.
このとき,$\rm A$点と$\rm B$点の力のモーメントの向きはどちらも$\rm O$を中心に反時計回りですね.
それでは,$\rm A$点における力のモーメントの大きさ$N_{\rm A}$と,$\rm B$点における力のモーメントの大きさ$N_{\rm B}$はそれぞれどのように表されるでしょうか?
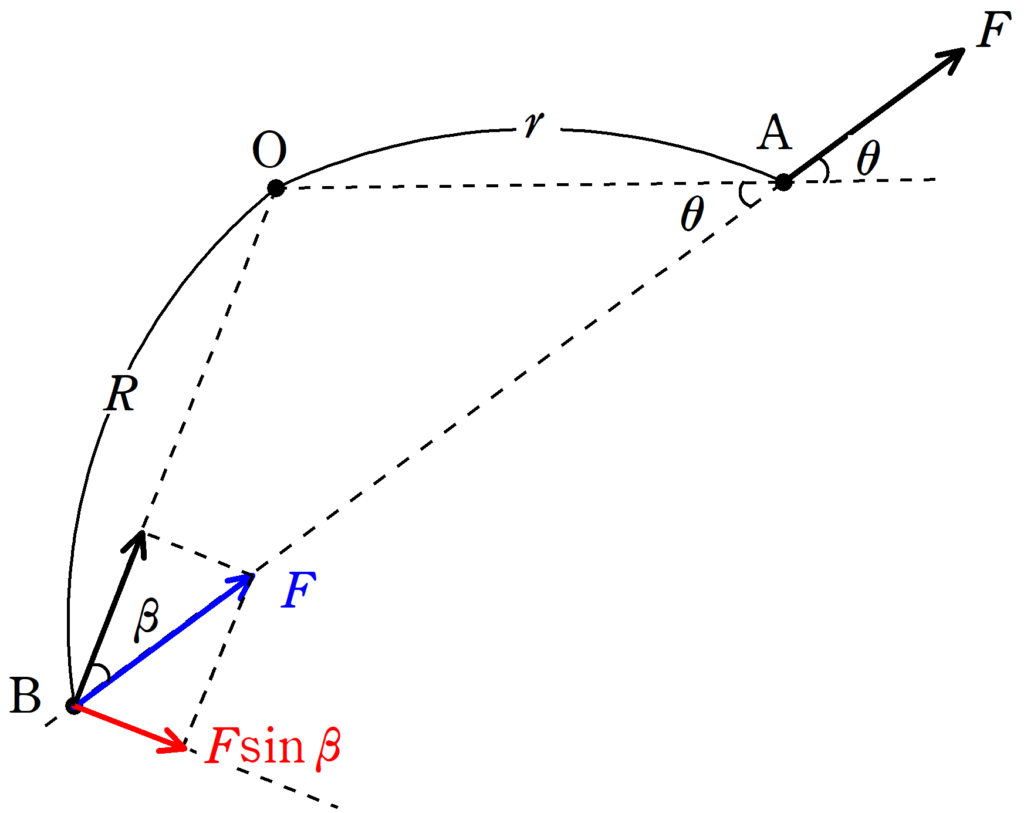

$N_{\rm A}$はさっきと同じで
$N_{\rm A}=rF\sin\theta$ $\dots (\ast)$
だね.
そして,点$\rm B$における力のモーメントの大きさは,力$F$を$\rm OB$方向とそれに垂直な方向に分解すれば
$N_{\rm B}=R\cdot F\sin\beta$ $\dots (2\ast)$
となるね.
なんか,$(\ast)$と$(2\ast)$は同じようには見えないな...

それでは,$\bigtriangleup \rm OAB$について,正弦定理の式を立ててみてください.

$\dfrac{R}{\sin\theta}=\dfrac{r}{\sin \beta}$
だね.
そうか,これを変形すると
$R\sin\beta =r\sin\theta$
だから$(2\ast)$に代入して
$N_{\rm B}=RF\sin\beta =rF\sin\theta$
となり,$(\ast)$と同じになるね!

はい.
ということで,作用線上であれば,どこに動かしても力のモーメントは等しくなります.
しかも,この証明をするときに物体がどこにあるかは関係ありませんでした.
使ったのは正弦定理くらいです.
したがって,物体の外にあっても力のモーメントの計算はできるのです.



コメント
[…] […]
[…] […]
[…] 作用線平行移動の原理[物体の外まで移動できる!?] […]