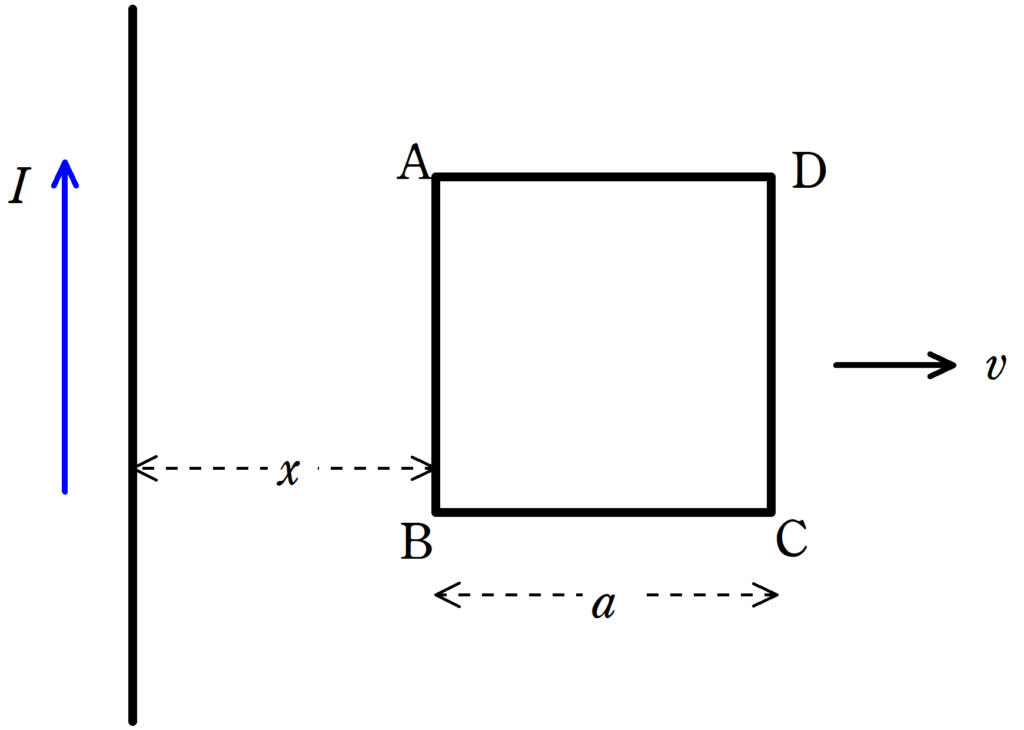
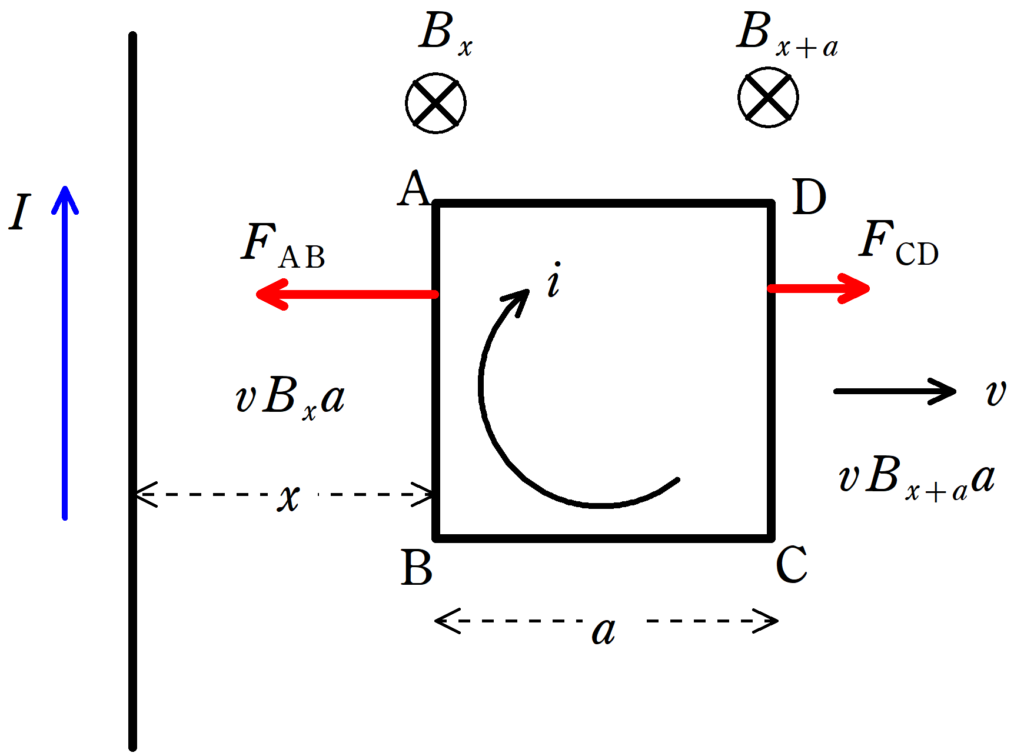
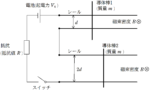
真空中で十分長い直線導線に大きさ$I$の定常電流を図の向きに流す．
さらに，一辺が$a$で全抵抗が$r$の正方形コイル$\rm ABCD$を用意し，$\rm AB$と十分長い直線導線が平行となるように，正方形コイルを一定の速さ$v$で図の向きを動かす．
ただし，コイルに流れる電流がつくる磁場は無視をする．また，真空での透磁率を$\mu_{0}$とする．
以下，十分長い導線とコイルとの距離が$x$のときのことを考える．
(1) コイルに流れる電流の大きさと向きを答えよ．
(2) コイルを等速度運動させるために，加える外力を求めよ．
(3) コイルの抵抗で生じる単位時間あたりのジュール熱を求めよ．
電流が流れるとまわりに磁場をつくるんだったね．
まずは直線電流がつくる磁場の復習をしよう！
十分長い直線電流が距離$r$の位置につくる磁場$H_{1}$は，導線に流れる電流の大きさを$I_{1}$とすると
$H_{1}=\dfrac{I_{1}}{2\pi r}$
向きは右ねじの法則にしたがいます．
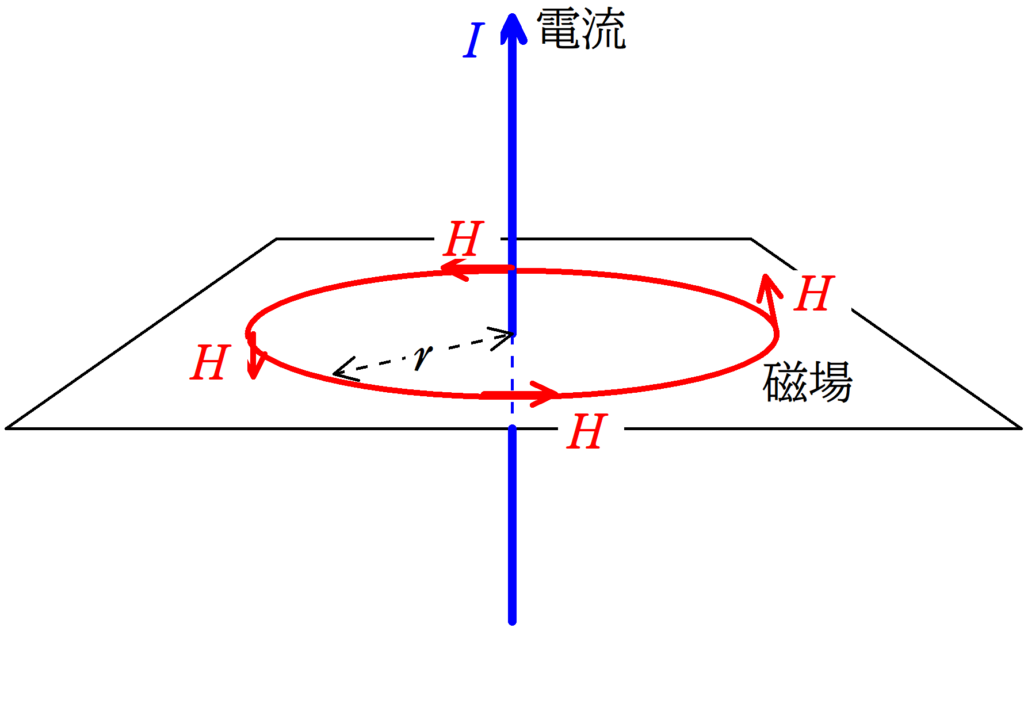
※ 右ねじの法則は右手の親指→電流，4本指→磁場 です．
そして，直線電流によってつくられる磁場内を導体棒が動いているので，導体棒が電池になります！
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は，PQの長さを$l$，PQ方向に垂直な速さを$v_{\perp}$，導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば，
$V=v_{\perp}Bl$
最後に，導体棒の問題で立てる式3つ！
これを意識できるといいですね．
- 回路の式（オームの法則，コンデンサーの基本式，電荷保存則など）
- 導体棒の運動に関する式（つり合いの式，運動方程式，運動量保存則など）
- 導体棒と回路の系全体のエネルギー収支の式
それでは，解いていきましょう．
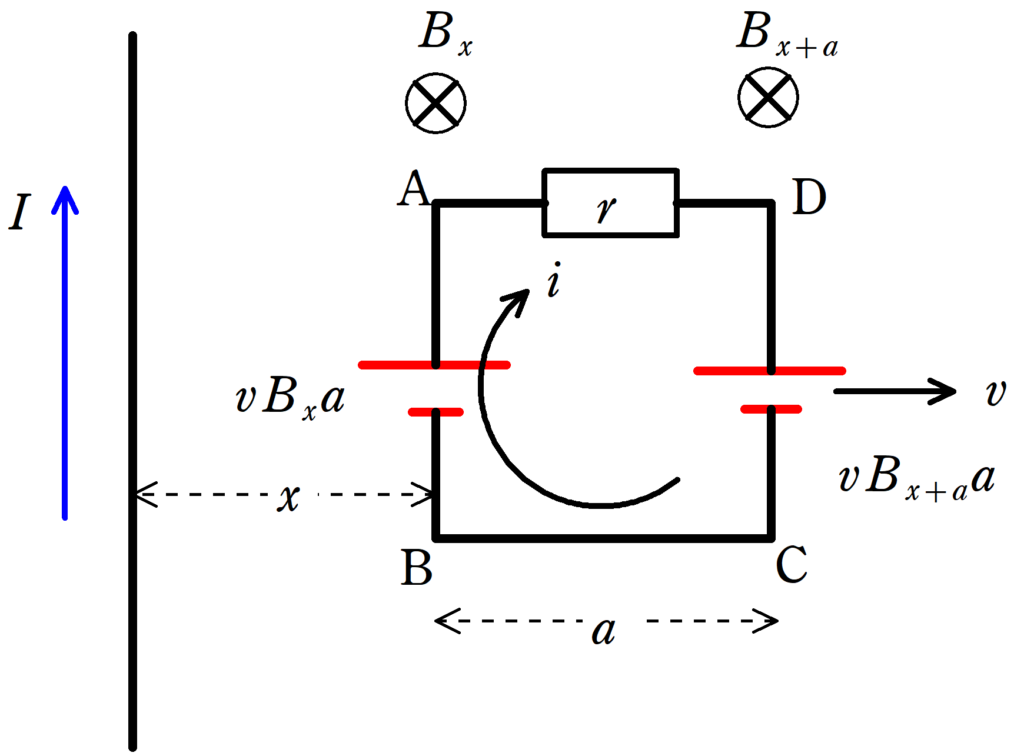
(1)
直線導線がつくる磁場は距離が遠くなると小さくなります．
つまり，$\rm AB$部分の磁場と$\rm CD$部分の磁場は異なります．
まず，十分長い直線電流がつくる磁場の式を使って，$\rm AB$部分の磁場$H_{x}$と$\rm CD$部分の磁場$H_{x+a}$を計算してみましょう．
★ 直線電流がつくる磁場の式
直線電流と$\rm AB$，$\rm CD$との距離はそれぞれ$x$，$x+a$なので，磁場$H_{x}$と$H_{x+a}$は
$H_{x}=\dfrac{I}{2\pi x}$
$H_{x+a}=\dfrac{I}{2\pi(x+a)}$
さらに，次の式を使って$\rm AB$部分と$\rm CD$部分の磁束密度$B_{x}$と$B_{x+a}$を計算しましょう．
磁束密度$B$と磁場$H$は，透磁率を$\mu$とすると
$B=\mu H$
の関係がある．
★ 磁束密度
$B_{x}=\mu_{0}H_{x}=\dfrac{\mu_{0}I}{2\pi x}$
$B_{x+a}=\mu_{0}H_{x}=\dfrac{\mu_{0}I}{2\pi (x+a)}$
これで，$\rm AB$部分と$\rm CD$部分の誘導起電力がわかります．
それぞれ起電力を$V_{\rm AB}$，$V_{\rm CD}$とすると，誘導起電力の式より次のようになります．
★ 導体棒に生じる誘導起電力
$V_{\rm AB}=vB_{x}a=\dfrac{\mu_{0}vIa}{2\pi x}$
$V_{\rm CD}=vB_{x+a}a=\dfrac{\mu_{0}vIa}{2\pi (x+a)}$
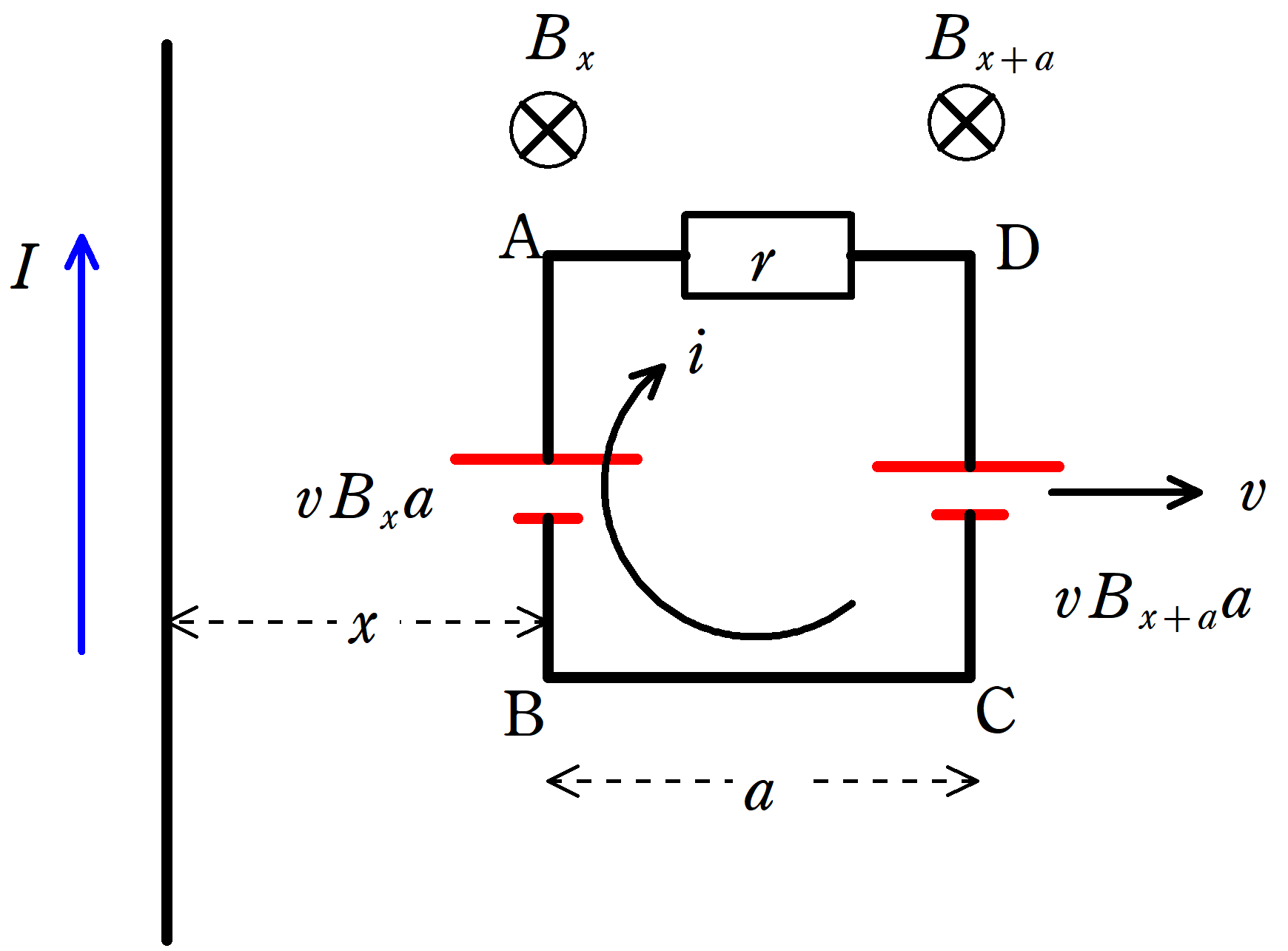
それでは，「1.回路の式」を立てましょう．
★ キルヒホッフの法則
回路に流れる電流を図の向きに$i$としましょう．
キルヒホッフの法則より
$\eqalign{V_{\rm AB}-V_{\rm CD}-ri&=0\cr ri&=\dfrac{\mu_{0}vIa}{2\pi x}- \dfrac{\mu_{0}vIa}{2\pi (x+a)}\cr i&=\dfrac{\mu_{0}vIa^{2}}{2\pi rx(x+a)}}$
したがって，(1)の答えは$i=\dfrac{\mu_{0}vIa^{2}}{2\pi rx(x+a)}$．向きは$\rm DCBA$の方向です．
(2)
次に，「2.導体棒の運動に関する式」を立てます．
今回は等速度運動をしているので，加速度0です．
すなわち，運動方程式
$ma=F$
の$a=0$を代入すればわかる通り，$F=0$となります．
つまり，つり合いの式ですね．
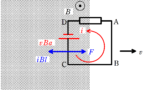
磁場中を電流が流れると電磁力を受けます．
電流の大きさを$I$，磁束密度の大きさを$B$とする．磁場の方向と電流の方向が垂直な関係にあるとき，導線の長さ$l$あたりにはたらく電磁力の大きさ$F$は
$F=IBl$
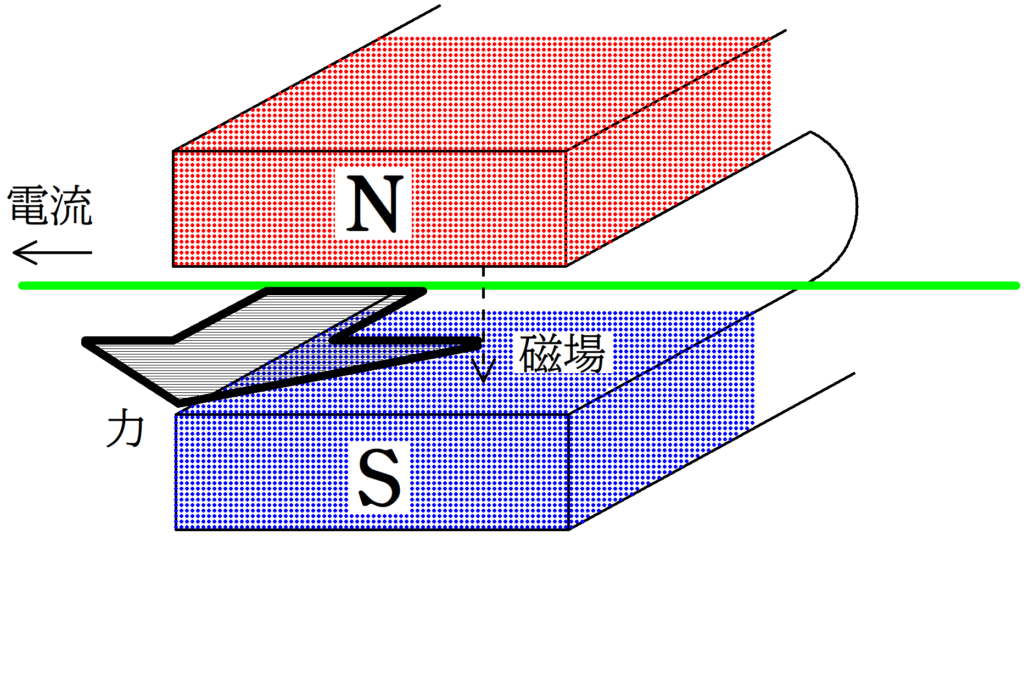
電磁力の向きはフレミング左手の法則にしたがいます．
※ 左手の親指→力の向き，人差し指→磁場の向き，中指→電流の向き
★ 電磁力
$\rm AB$と$\rm CD$にかかる電磁力の向きは上図のようになります．
それぞれの力の大きさ$F_{\rm AB}$と$F_{\rm CD}$は
$F_{\rm AB}=iB_{x}a=\dfrac{\mu_{0}^{2}vI^{2}a^{3}}{4\pi^{2}rx^{2}(x+a)}$
$F_{\rm CD}=iB_{x+a}a=\dfrac{\mu_{0}^{2}vI^{2}a^{3}}{4\pi^{2}rx(x+a)^{2}}$
以上より，コイルにはたらく電磁力の合力$F$は，右向きを正として
$\eqalign{F&=F_{\rm CD}-F_{\rm AB}\\&=\dfrac{\mu_{0}^{2}vI^{2}a^{3}}{4\pi^{2}rx(x+a)^{2}}-\dfrac{\mu_{0}^{2}vI^{2}a^{3}}{4\pi^{2}rx^{2}(x+a)}\\&=-\dfrac{\mu_{0}^{2}vI^{2}a^{4}}{4\pi^{2}rx^{2}(x+a)^{2}}}$
したがって，合力を0にする外力$F^{\prime}$は
$F^{\prime}=\dfrac{\mu_{0}^{2}vI^{2}a^{4}}{4\pi^{2}rx^{2}(x+a)^{2}}$
向きは図の右向きですね．
(3)
最後は「3.エネルギー収支の式」を立てましょう．
導体棒の運動エネルギーや位置エネルギーは変化していません．
すなわち
外力がした仕事率=単位時間当たりの抵抗で生じるジュール熱
となります．
電磁力がした仕事や誘導起電力がする仕事を入れない理由はこちらです．
求める単位時間あたりのジュール熱を$Q$として
$Q=Fv=\dfrac{\mu_{0}^{2}v^{2}I^{2}a^{4}}{4\pi^{2}rx^{2}(x+a)^{2}}$
コメント