
前回の内容はこちらです.

運動方程式は以下の式のことをいいます.
前回は運動方程式を扱いました.
質量$m$の物体に力$F$がはたらいているとき,物体の加速度$a$をすると,次の関係式が成り立つ.
$ma=F$
これを運動方程式という.

また,運動方程式を立てる手順は次のようになります.
運動方程式を立てる際には
1. +の向きを決め,その+の向きを加速度の向きとする.
2. 物体の速度の向きとは関係なく,はたらく力をかき,運動方程式を立てる.
3. 力の向きは1.で決めた正の方向であれば,正とし,負の方向に向いていれば負としてかく.

特に,
「2. 物体の速度の向きとは関係なく,はたらく力をかき,運動方程式を立てる.」
が間違いやすいよ!

では,問題を解いていきましょう.
今回は,1段レベルアップして,力を分解して運動方程式を立てます.
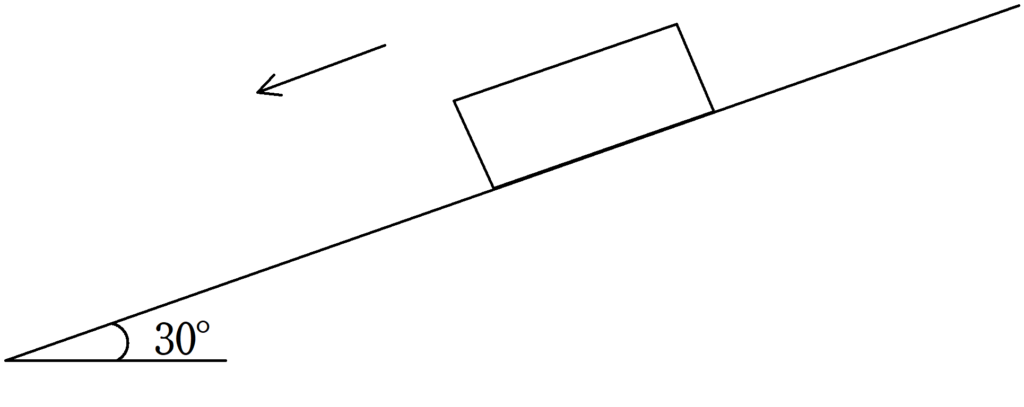
上図のように,傾角30°のなめらかな斜面上に質量$m$の物体が置かれ,静かに手をはなしたところ,物体は動き出し,加速度運動をした.
このとき,斜面下方向の加速度を$a$として運動方程式を立て,加速度を求めよ.
ただし,重力加速度の大きさを$g$とする.
<解答>

問題文によると,斜面下向きを正とするんだね.
まず,物体にはたらく力をかいてみよう.
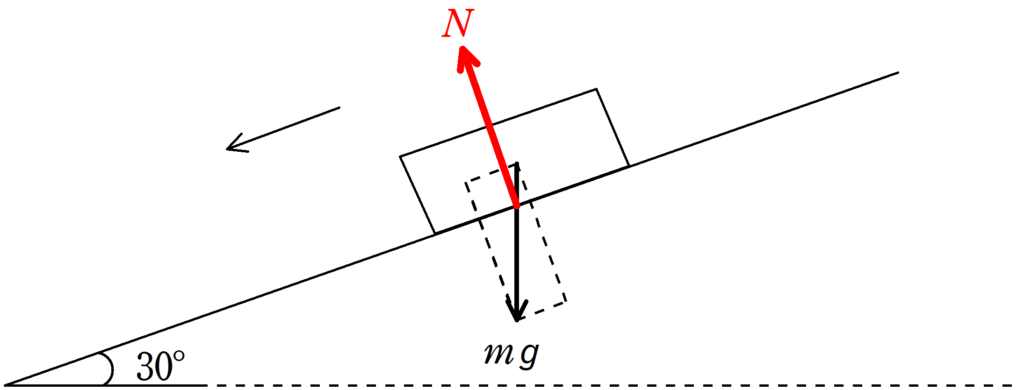

まずは,重力をかきましょう.
重力は鉛直下向きで大きさは$mg$です.
じつは,重力加速度の大きさは場所によって違います.
地球だと大体$g=9.8(\rm m/s^{2})$となっています.

また,その他の力は物体に接触している部分をみれば予想ができます.
今回は斜面と接触しているので,垂直抗力がはたらきます.
垂直抗力は,少し難しく言うと束縛条件から決まるのですが,今回は斜面に垂直高な方向のつり合いの式で垂直抗力の大きさを決めましょう.

そして,つり合いの式を立てるために,重力を斜面に平行な方向と垂直な方向に分解しましょう.
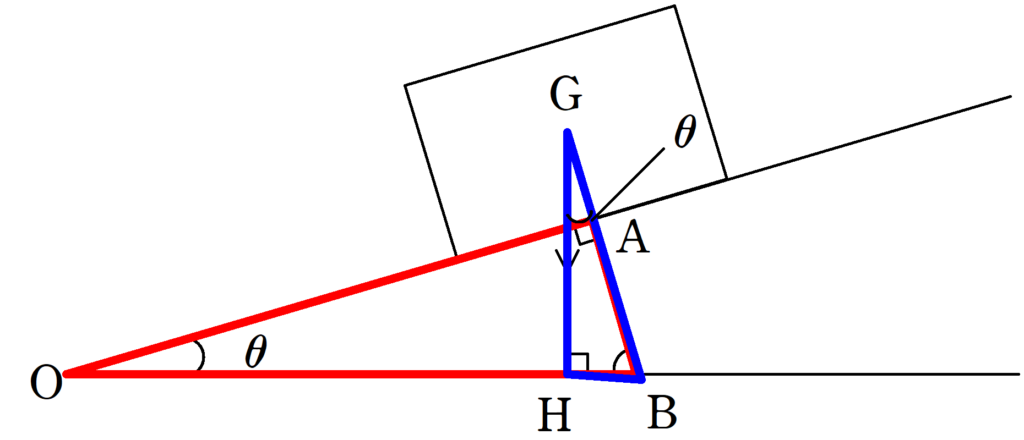
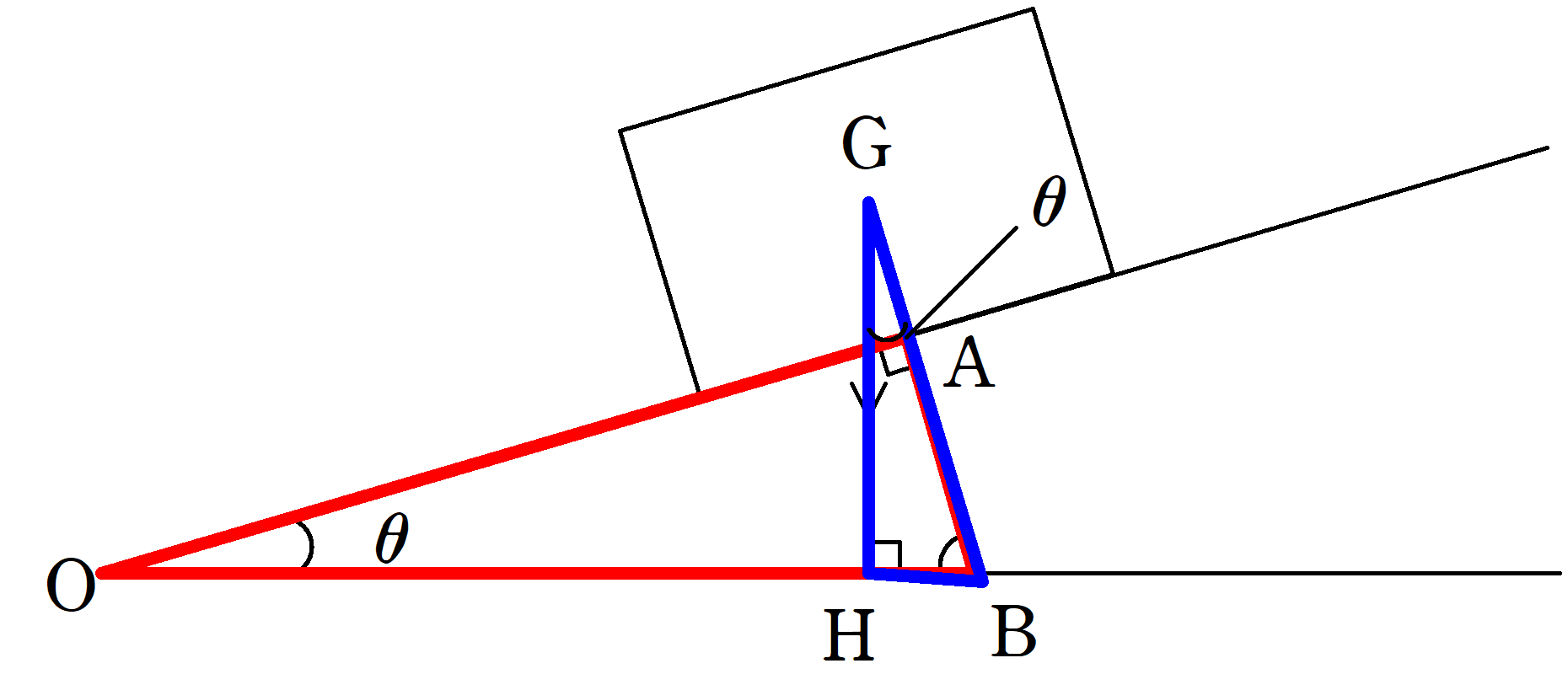
そのためには,次図のように斜面の角度が$\theta$のときに,
$\rm \triangle OAB$∽$\rm \triangle GHB$
より,$\rm \angle BGH=\theta$となります.
これはよくでるので覚えておいてもよいでしょう.

また,斜辺の長さがわかっているときの底辺と高さを求める計算は物理でよく出てくるので覚えておくとよいでしょう.
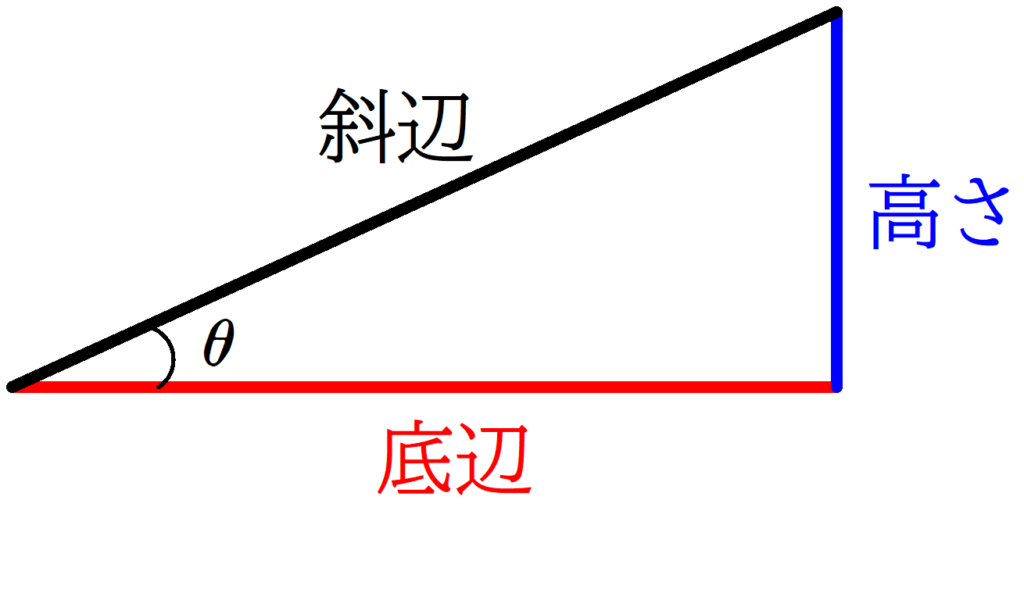
★ 底辺について
$\cos\theta =\dfrac{底辺}{斜辺}$ $\therefore$ 底辺$=$斜辺$\cos\theta$
★ 高さについて
$\sin\theta =\dfrac{高さ}{斜辺}$ $\therefore$ 高さ$=$斜辺$\sin\theta$

これらのことを使うと,重力$mg$は次のように分解できるんだね.
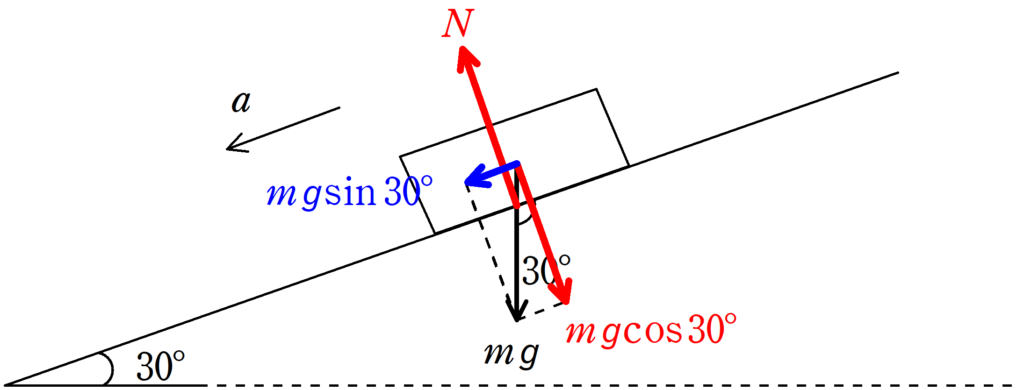

斜面に平行な方向が$mg\sin 30°$,垂直な方向は$mg\cos 30°$だね.
ちなみに,
$\cos 30°=\dfrac{\sqrt{3}}{2}$,$\sin 30°=\dfrac{1}{2}$
だね.下図で確認してね.

だから,斜面に平行な方向が$\dfrac{1}{2}mg$,垂直な方向は$\dfrac{\sqrt{3}}{2}mg$だね.

以上のことから,斜面平行な方向の運動方程式は次のようになるね.
斜面平行下向きを正とした加速度を$a$とすると
★ 斜面平行方向の運動方程式
$ma=\dfrac{1}{2}mg$
$a=\dfrac{1}{2}g$

コメント
[…] […]
[…] […]