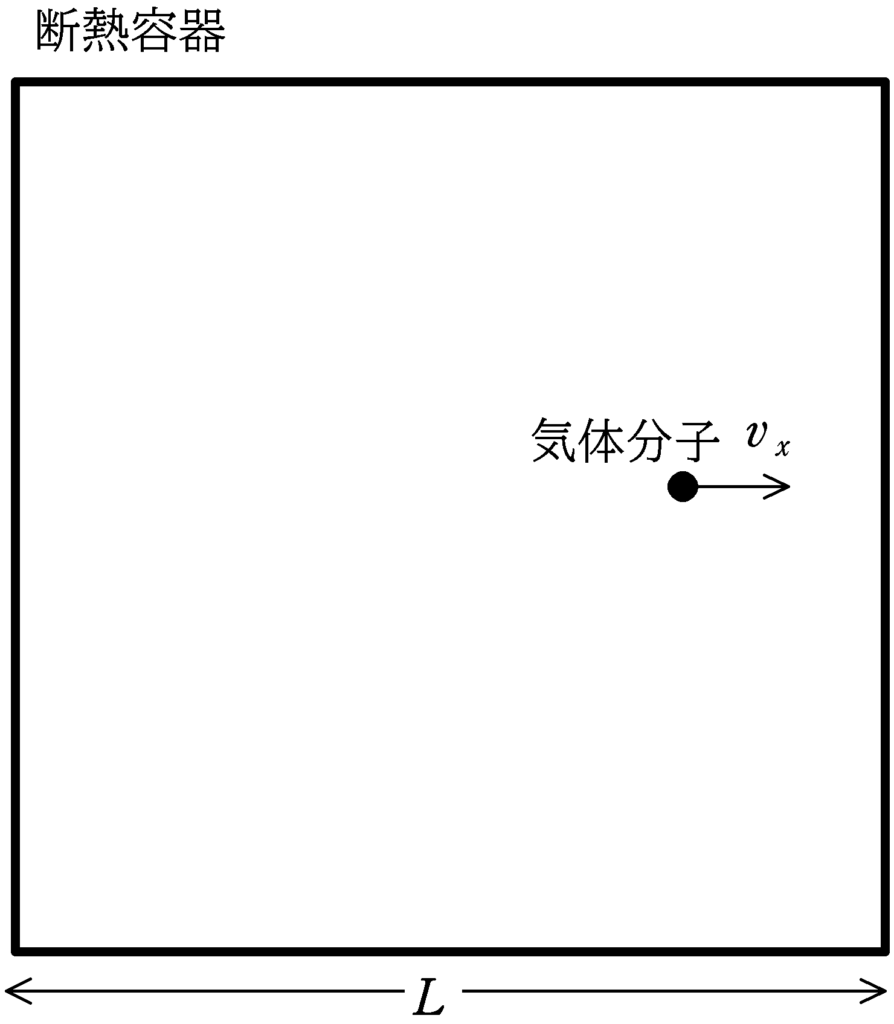
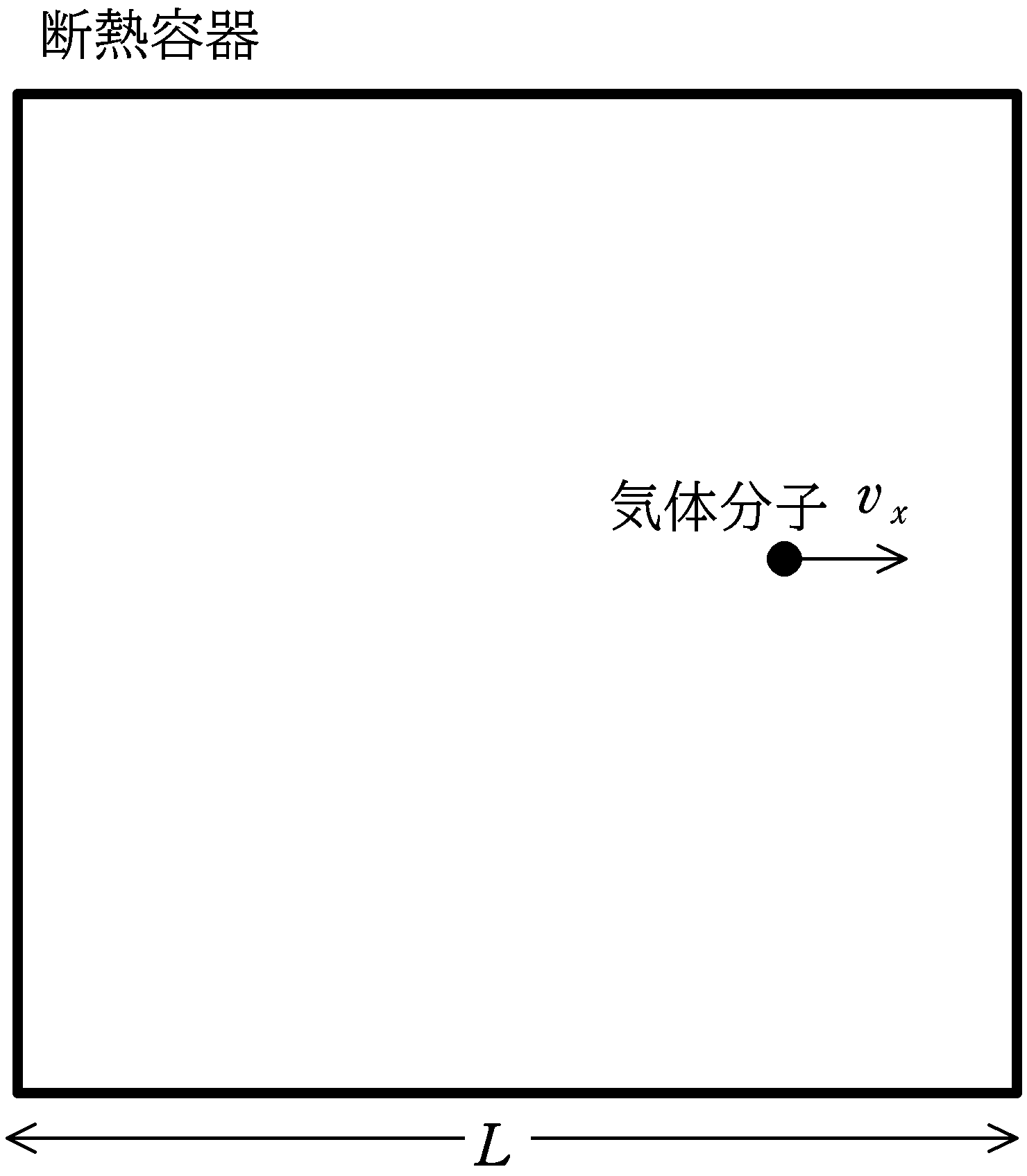
図のように横幅$L$の断熱容器の中に質量$m$の気体分子が衝突を繰り返して往復運動をしている．気体分子は衝突面と垂直な速度をもっており，その速さは$v_{x}$である．衝突はすべて完全弾性衝突をするものとして次の問いに答えよ．
(1) 気体分子が1回衝突する際に壁に与える力積の大きさを求めよ．
(2) 気体分子が右側の壁と1回衝突するのにかかる時間を求めよ．
(3) 気体分子が時間$\varDelta t$の間に右側の衝突する回数を求めよ．
(4) 気体分子が$\varDelta t$の間に右側の壁に与える力積の総和を求めることで，$\varDelta t$の間に気体分子が右側の壁に与える平均の力の大きさを求めよ．
<解答>
(1) 壁は静止していて，完全弾性衝突をするので，衝突によって向きは変えるが速さは変化しない．
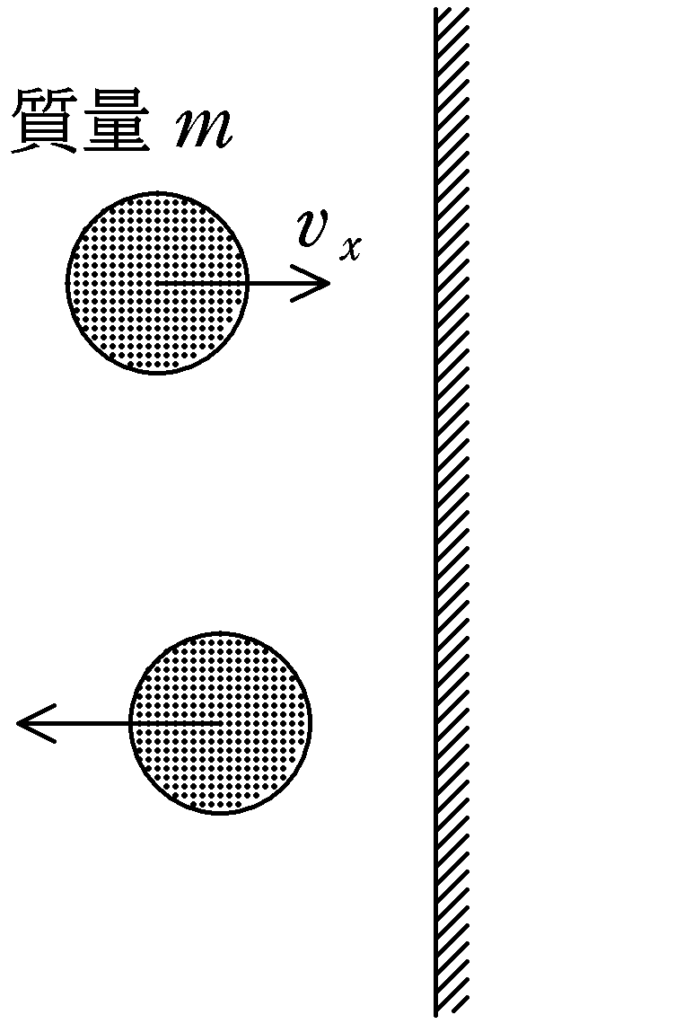
右側の壁に当たる直前の速度を$v_{x}$とすると，衝突後の速度は$-v_{x}$．
運動量変化と力積の関係より，気体分子が受ける力積は
気体分子が受ける力積$=m\times (-v_{x})-mv_{x}=-2mv_{x}=-2mv_{x}$
作用反作用の法則より，壁が受ける力積は$2mv_{x}$でその大きさも$2mv_{x}$(答)
(2)
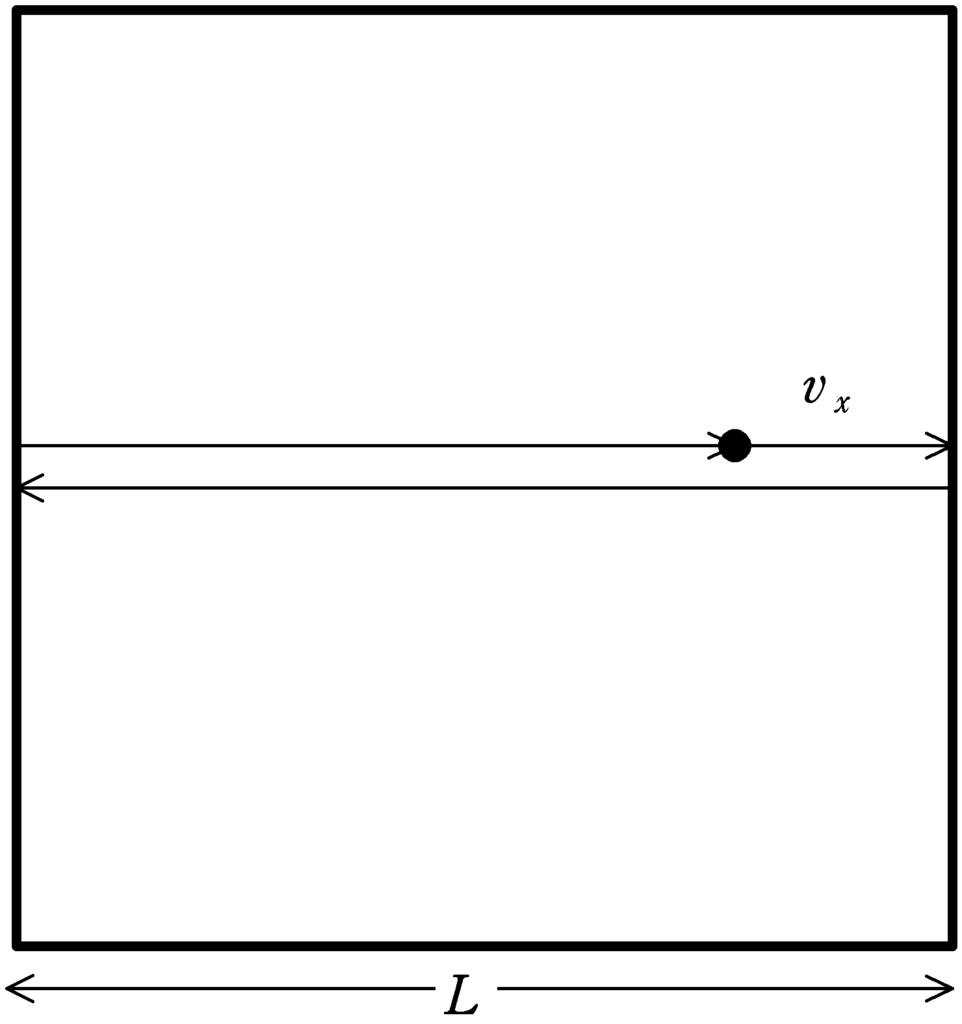
往復距離は$2L$なので，1回衝突するのにかかる時間は$\dfrac{2L}{v_{x}}$(答)
(3) 比例式を考える．時間$\varDelta t$の間に右側の壁と衝突する回数$A$は
$1\,[回数]\,：\,\dfrac{2L}{v_{x}}\,[時間]\,=\,A\,[回数]\,：\,\varDelta t\,[時間]$
$\therefore\,\, A=\dfrac{v_{x}}{2L}\varDelta t$(答)
(4) 1回の衝突で壁に与える力積の大きさが$2mv_{x}$で，これが$\varDelta t$の間に$\dfrac{v_{x}}{2L}\varDelta t$回ぶつかるので
力積の和$=2mv_{x}\times \dfrac{v_{x}}{2L}\varDelta t=\dfrac{mv_{x}^{2}}{L}\varDelta t$
力積の和を（平均の力）$\times \varDelta t$とみなす．平均の力の大きさを$F$とすれば
$F\varDelta t=\dfrac{mv_{x}^{2}}{L}\varDelta t$
$\therefore\,\, F=\dfrac{mv_{x}^{2}}{L}$(答)
コメント