気体分子運動論基礎の基礎4 | Physicmath（フィジクマス）

PHYさん

前回の内容はこちらです．

前回と同じ問題を今回は文字で考えていきます．

問題

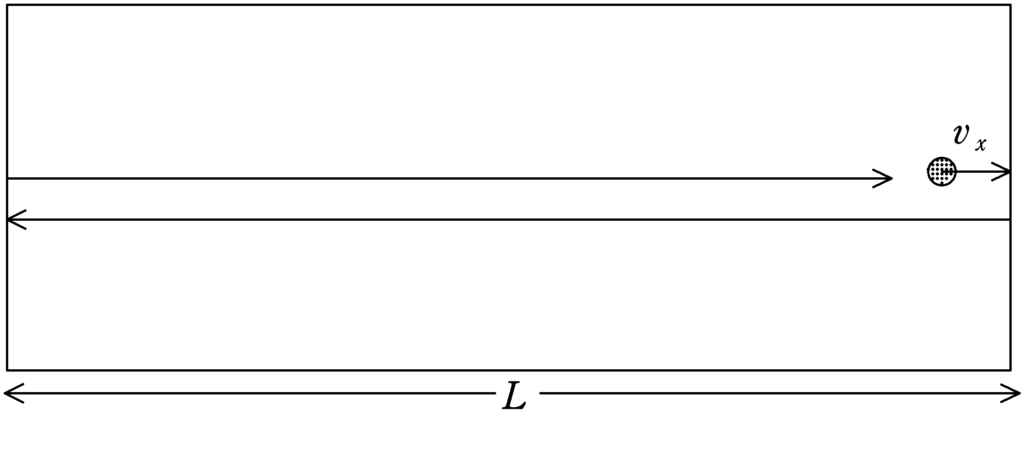
物体が一定の速さ$v_{x}$で幅$L$の部屋を何度も往復している．このとき，次の問いに答えよ．

(1)　一度壁にぶつかってから，往復して再び同じ壁にぶつかるまでの時間を求めよ．

(2)　時間$T$の間に上図の右側の壁にあたる回数を求めよ．

<解答>

(1)

NEKO

往復距離は$2L$で物体の速さが$v_{x}$だから

距離$=$速さ$\times $時間

の関係を使ってみましょう．求める時間を$\varDelta t$として

$2L=v_{x}\times \varDelta t$

$ \varDelta t=\dfrac{2L}{v_{x}}$ (答)

(2)　　

NEKO

比例式で考えましょう．

(1)より，右側の壁と1回衝突する時間が$\varDelta t=\dfrac{2L}{v_{x}}$なので，時間$T$の間に衝突する回数$A$は，

$1[回数]\,：\,\dfrac{2L}{v_{x}}\,[時間]\,=\,A\,[回数]\,：\,T\,[時間]$

$A\times \dfrac{2L}{v_{x}}=1\times T$

$\therefore\,\, A=\dfrac{v_{x}}{2L}$ (答)

PHYさん

次回はここまでの流れを一気に確認する問題を扱います．

気体分子運動論　基礎の基礎4