$X$の問題2　滑車による運動と衝突

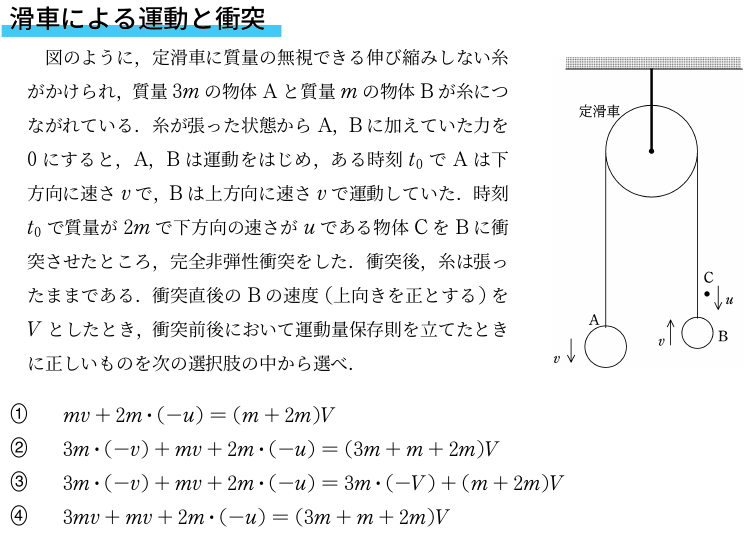
＜問題＞

<解答>

ポイントは次の2つです．

まず，「ポイント1」ですが，運動量保存則を立てる物体系は「AとBとC」の3つにしなくてはいけません．

いま，CがBと衝突し，この衝突によってBの速度が急激に変化するわけですが，糸が滑車を介してAにつながっており，同時にAの速度も急激に変化します．Aの速度が急激に変化するので，張力が「撃力」となるため，BとCだけを対象とすると，Bに張力による撃力がはたらき，運動量が保存しなくなります．

ちなみに運動量保存則が成り立つ条件はこちらの記事でも書いてあります．

「AとBとC」を対象にすれば，張力の力の和が$0$になるので，運動量が保存します．

次に「ポイント2」ですが，これは「ポイント1」でも話しましたが，張力の和が0になるには，Aの速度（と力）の正の向きをBと反対方向にとらないといけません．

もし，Aも上向きを正にとると，張力の大きさを$T$とすれば，$T+T=2T$となってしまいます．

したがって，答えは④になります．

①はBとCだけを系にとっているので×です．

②はAはB，Cの速度の向きと反対にとっていないので×です．

③も②と同じ理由で×です．

したがって，答えは④になります．

では，仮にすべての速度の向きを正にとったときはどのように考えればいいのかを考えていきたいと思います．

Aについて，衝突前後での「運動量変化と力積」の関係式を立てます．衝突後のBの速度を$V$としていて，AとBの束縛条件(AとBの速度の向きが反対で大きさが同じ)を考えれば，衝突後のAの速度は$-V$です．重力による力積は非常に小さいので無視します．張力による力積を$I_{T}$，上向きを正にとって式を立てると

$3m\cdot (-V)-3m\cdot (-v)=I_{T}$　$\cdots (\ast)$

Bについても「運動量変化と力積」の関係式を立てます．張力による力積は$I_{T}$でCとの衝突によるBが受ける力積は$I$とします．重力の力積は無視します．

$mV-mv=I_{T}+I$　$\cdots (2\ast)$

Cについても「運動量変化と力積」の関係式を立てます．衝突によりCが受ける力積は「作用反作用の法則」から$-I$と書けます．重力の力積は無視します．

$2mV-2m\cdot (-u)=-I$　$\cdots (3\ast)$

$(\ast)，(2\ast)，(3\ast)$から，$I_{T}$と$I$を消去した式が「運動量保存則」です．$(\ast)-(2\ast)-(3\ast)$を計算すればうまく消えます．

$3m\cdot (-V)-3m\cdot (-v)-\{mV-mv \}-\{2mV-2m\cdot (-u)\}=0$

$\therefore\,\, 3mv+mv+2m\cdot (-u)=(3m+m+2m)V$

このように，運動量保存則を示す際に用いる「運動量変化と力積」の関係を使えば理解ができます．

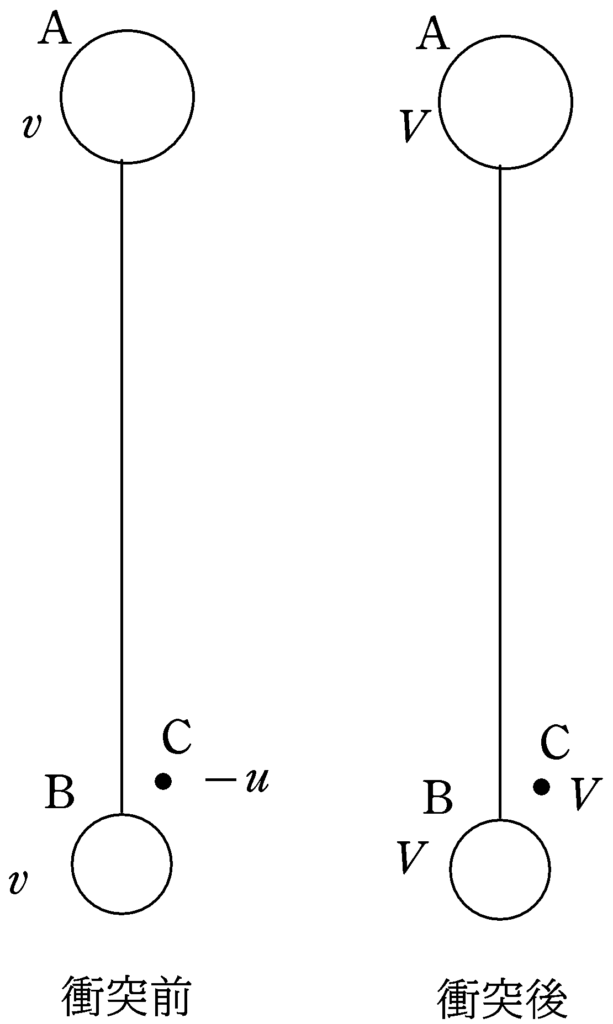
ただ，もっと感覚的に立てたい場合もあると思うので，今回のようなシンプルな問題ではAを便宜的にBの上側にもってきて，下図のように考えてもいいかと思います．