
前回の内容はこちらです.
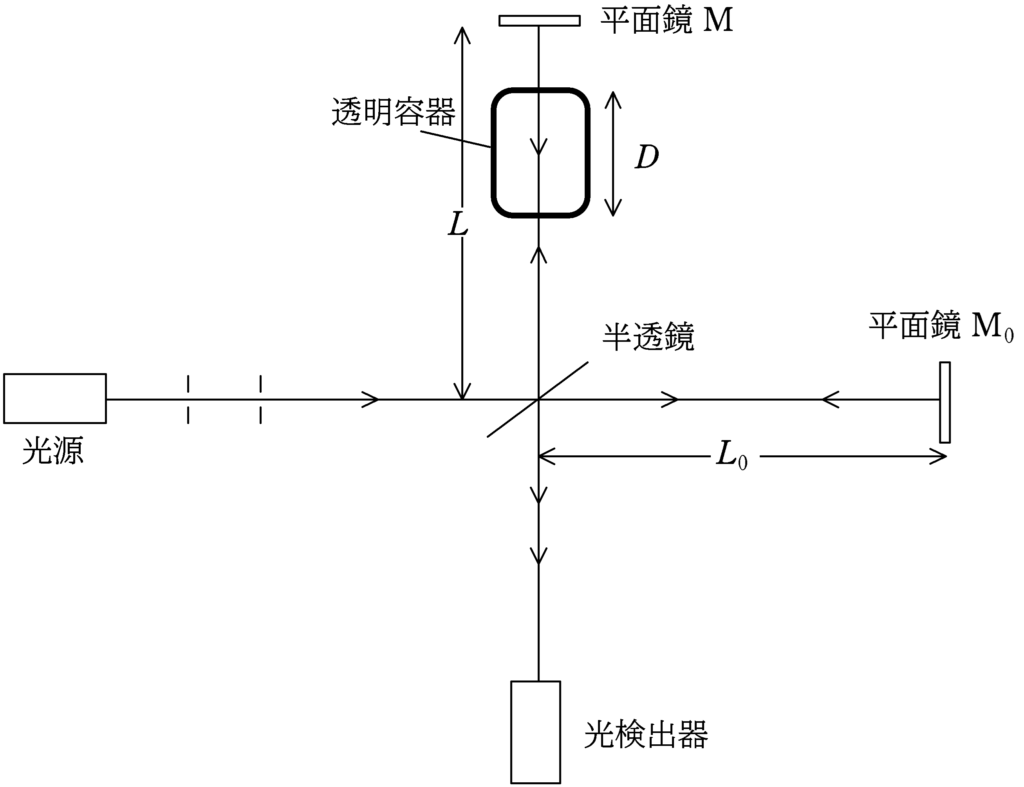
図に示す装置で光の干渉の実験を行う.単色光源を出た波長$\lambda$の光は半透鏡で2つに分けられ,一方は平面鏡$\rm M$で反射されて,同じ経路をもどり,その一部が半透鏡を通過して光検出器に到達する.他方は平面鏡$\rm M_{0}$で反射されて同じ経路をもどり,その一部が半透鏡で反射されて光検出器に到達し,鏡Mからの光と干渉する.物質の水溶液濃度$p$とその屈折率の間に,$n=n_{0}+kp$($k$は物質固有の定数,$n_{0}$は水の屈折率)の関係があるとき,この装置を用いて物質の水溶液濃度を測定することができる.手順は以下の通りである.
手順1 半透鏡と$\rm M$の間に置かれた長さ$D$の透明な容器に水を入れ,検出器での光の強度が最大になる位置に$\rm M$の位置を調整した.
手順2 透明な容器の中に物質を少しずつ入れていくと検出器の強度が最大と最小を繰り返す.物質を入れてから検出器の強度が$m$回目に最大となった.
このとき,水溶液の濃度$p$を$m,\lambda,k,D$を用いて表せ.

干渉による位相差の条件をまとめると次のようになります.
地点Pにおける2つの波の位相差を$\phi$,整数を$m$とすると,
強め合いの条件:$\phi=2\pi m$
弱め合いの条件:$\phi=(2m+1)\pi $
位相差$\phi$は次の3つの要素で決まる.
$\phi_{1}$:初期位相のずれ
同位相なら$\phi_{1}=0$,逆位相なら$\phi_{1}=\pi$
$\phi_{2}$:反射による位相のずれ
自由端反射なら$\phi_{2}=0$,固定端反射なら$\phi_{2}=\pi$
$\phi_{3}$:距離の差(屈折率が変わることで生じる光学的な距離の差を含む)による位相のずれ
距離の差が$\Delta l$のとき,次の比例式を立てて,位相差$\phi_{3}$を計算する.
$2\pi : \lambda =\phi_{3} : \Delta l$
$\therefore \phi_{3}=\dfrac{2\pi}{\lambda}\Delta l$
このとき,位相差$\phi$は
$\phi=\phi_{1}+\phi_{2}+\phi_{3}$

ちなみに,途中で使う屈折の法則はこちら
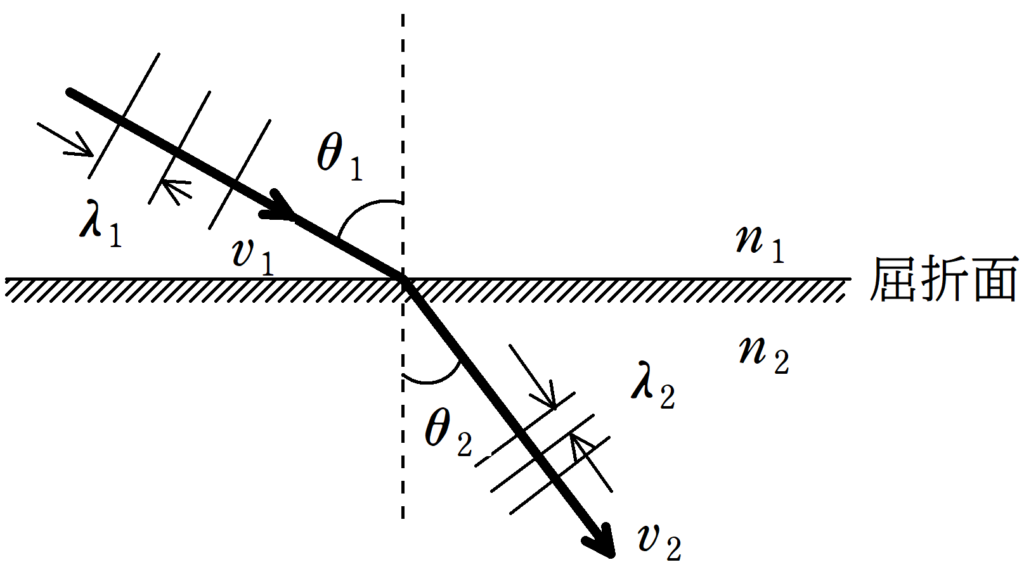
速さ$v_{1}$,波長$\lambda_{1}$の波が入射角$\theta_{1}$で屈折面に入射し,その後屈折角が$\theta_{2}$,速さ$v_{2}$,波長が$\lambda_{2}$となった.入射側の媒質の屈折率を$n_{1}$,屈折する側の媒質の屈折率を$n_{2}$とすると,次の関係が成り立つ.
$\dfrac{v_{1}}{v_{2}}=\dfrac{\sin\theta_{1}}{\sin\theta_{2}}$
また,屈折により,媒質の振動数$f$および周期$T$は変化しないことから,次のことが成り立つ.
$\dfrac{v_{1}}{v_{2}}=\dfrac{\cancel{f}\lambda_{1}}{\cancel{f}\lambda_{2}}=\dfrac{\lambda_{1}}{\lambda_{2}}$
一方,屈折率との関係は次のようになる.
$n_{1}\sin\theta_{1}=n_{2}\sin\theta_{2}$
$n_{1}v_{1}=n_{2}v_{2}$
$n_{1}\lambda_{1}=n_{2}\lambda_{2}$
最後に,$n_{12}=\dfrac{n_{2}}{n_{1}}$を屈折率$n_{1}$の媒質に対する屈折率$n_{2}$の媒質の相対屈折率という.
<解答>
※ 実際は半透鏡での反射によって,2経路の位相差が$\pi$分ずれ,強め合いの条件と弱め合いの条件が真逆になりますが,差をとると同じ答えが出ます.

まずは,手順1について立式していきましょう.
手順1「半透鏡と$\rm M$の間に置かれた長さ$D$の透明な容器に水を入れ,検出器での光の強度が最大になる位置に$\rm M$の位置を調整した.」
水内での屈折率$\lambda_{1}$は屈折の法則より,$\lambda_{1}=\dfrac{\lambda}{n_{0}}$です.位相差を考える際は,空気内と水内で波長が異なるので分けて考える必要があります.

整数$l$を用いて,強め合いの条件を立てます.
★ 強め合いの条件
$\dfrac{2\pi}{\lambda}\{2(L_{1}-D)\}+\dfrac{2\pi}{\lambda_{1}}\cdot 2D-\dfrac{2\pi}{\lambda}\cdot 2L_{0}=2\pi l \cdots (\ast)$

次に手順2を立式します.
手順2 「透明な容器の中に物質を少しずつ入れていくと検出器の強度が最大と最小を繰り返す.物質を入れてから検出器の強度が$m$回目に最大となった.」
液体濃度を$p$とすると,屈折率$n$は,問題文より,$n=n_{0}+kp$になることから,液体の波長は$\lambda_{2}=\dfrac{\lambda}{n_{0}+kp}$となります.$(\ast)$の左辺の式は$\lambda_{1}\to \lambda_{2}$になるだけです.また,問題文によると$m$回明るくなったことから,$(\ast)$の右辺は$2\pi l\to 2\pi(l+m)$にすればよいでしょう.
★ 強め合いの条件
$\dfrac{2\pi}{\lambda}\{2(L_{1}-D)\}+\dfrac{2\pi}{\lambda_{2}}\cdot 2D-\dfrac{2\pi}{\lambda}\cdot 2L_{0}=2\pi (l+m) \cdots (2\ast)$

$(2\ast)-(\ast)$を計算すると邪魔なものがごそっと消えます.
$(2\ast)-(\ast)$
$\dfrac{\cancel{2\pi} \times 2D}{\lambda_{2}}-\dfrac{\cancel{2\pi} \times 2D}{\lambda_{1}}=\cancel{2\pi} m$

$\lambda_{1}=\dfrac{\lambda}{n_{0}}$と$\lambda_{2}=\dfrac{\lambda}{n_{0}+kp}$を代入しましょう.代入する際はあらかじめ逆数をとった
$\dfrac{1}{\lambda_{1}}=\dfrac{n_{0}}{\lambda}$
$\dfrac{1}{\lambda_{2}}=\dfrac{n_{0}+kp}{\lambda}$
を計算しておくとよいでしょう.
$2D\times \dfrac{n_{0}+kp}{\lambda}-2D\times\dfrac{n_{0}}{\lambda}= m $
$\lambda$をかけて式を整理すると
$2Dkp=m\lambda$ $\therefore\,\, p=\dfrac{m\lambda}{2kD}$ (答)

つまり,光の強度が最大になる数を数えれば,液体の濃度を計算できるんだね.





コメント