
前回の内容はこちらです.

また,平面波の図を書く練習をしたい人はこちらもどうぞ.
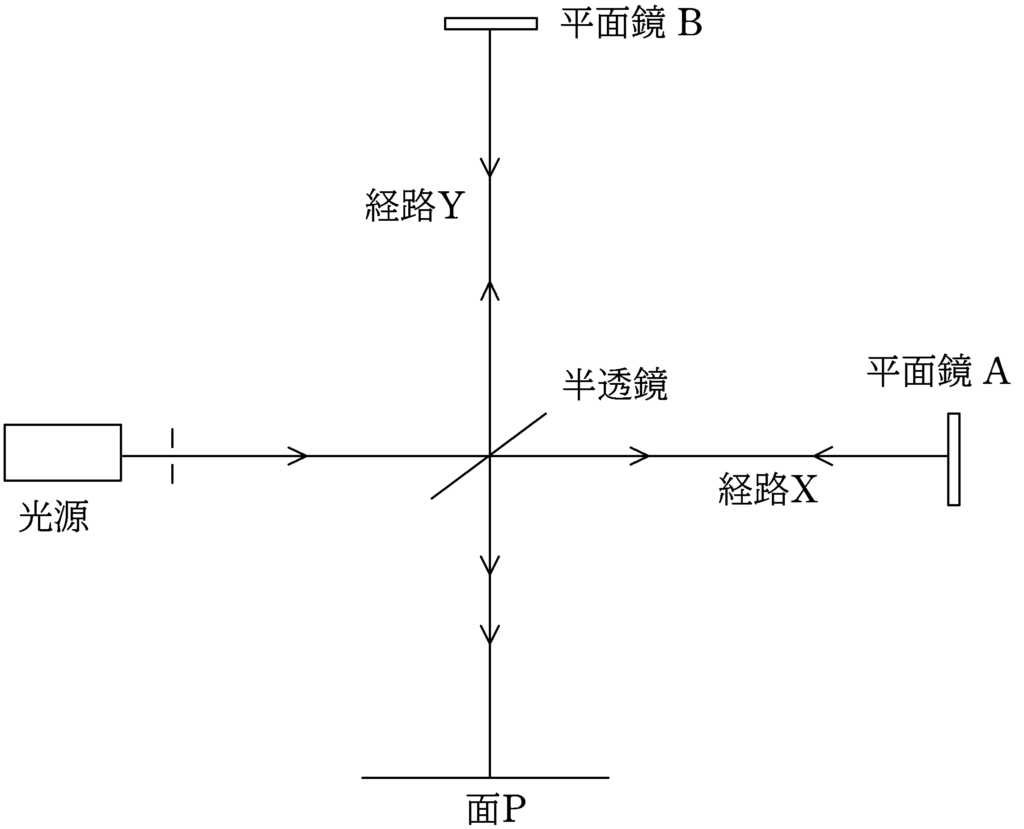
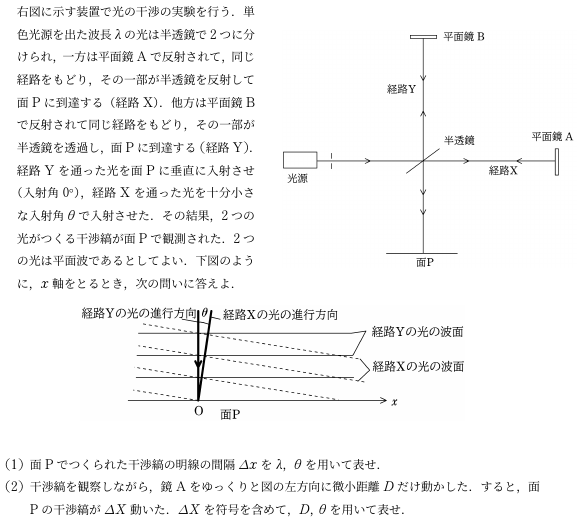
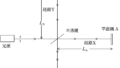
上図に示す装置で光の干渉の実験を行う.単色光源を出た波長$\lambda$の光は半透鏡で2つに分けられ,一方は平面鏡$\rm A$で反射されて,同じ経路をもどり,その一部が半透鏡を反射して面Pに到達する(経路$\rm X$).他方は平面鏡$\rm B$で反射されて同じ経路をもどり,その一部が半透鏡を透過し,面Pに到達する(経路$\rm Y$).経路$\rm Y$を通った光を面Pに垂直に入射させ(入射角$0^{\circ}$),経路Xを通った光を十分小さな入射角$\theta$で入射させた.その結果,2つの光がつくる干渉縞が面Pで観測された.2つの光は平面波であるとしてよい.下図のように,$x$軸をとるとき,次の問いに答えよ.
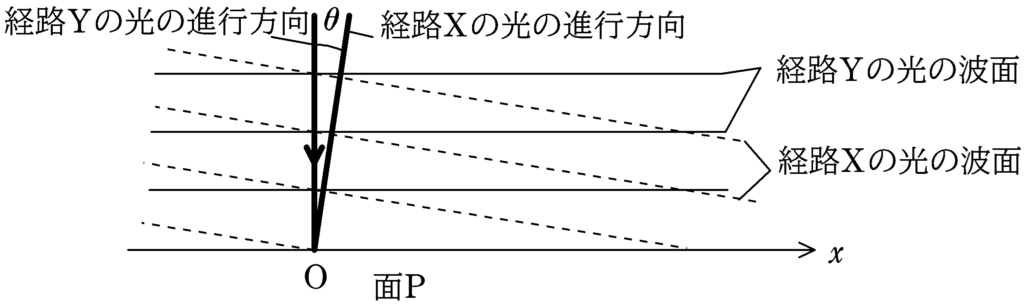
(1) 面Pでつくられた干渉縞の明線の間隔$\varDelta x$を$\lambda$,$\theta$を用いて表せ.
(2) 干渉縞を観察しながら,鏡Aをゆっくりと図の左方向に微小距離$D$だけ動かした.すると,面Pの干渉縞が$\varDelta x$動いた.$\varDelta x$を符号を含めて,$D,\theta$を用いて表せ.
<解答>
(1)

平面波の問題をなるべく
- 大きく
- 丁寧に
図をかくとよいでしょう.また,2つの平面波の交点は速さが同じとき,それぞれの波面の角の2等分線の方向に移動することを確認しておきましょう.
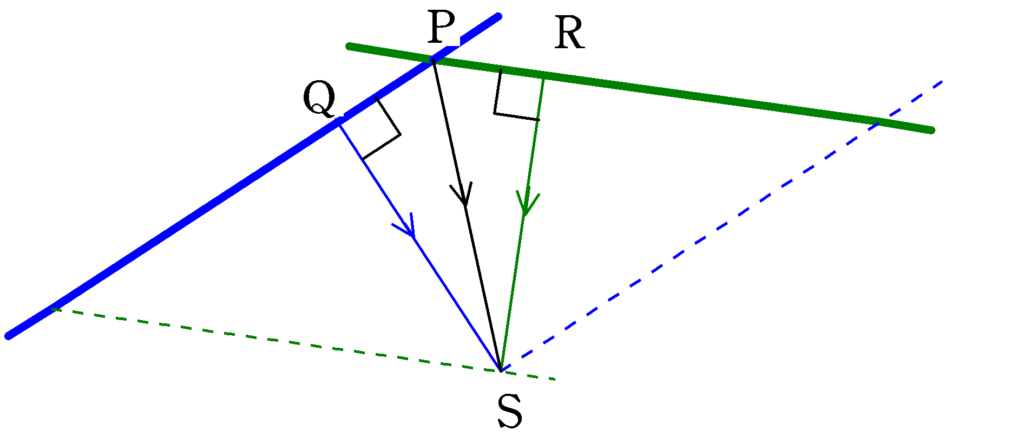

上図は青の波面(太線),緑の波面(太線)の交点Pが,それぞれの波面の移動によって,Sに移動する様子をかいてあります.青の波面と緑の波面の速さは等しいので,上図において
$\rm QS=RS$
であり,$\rm PS$が共通で,$\angle{\rm PQS}=\angle{\rm PRS}=90^{\circ}$であるから,直角三角形の合同条件より,$\bigtriangleup{\rm PQS}$と$\bigtriangleup{\rm PRS}$は合同です.したがって,対応する角が等しいので$\angle{\rm QPR}=\angle{\rm RPS}$となり,確かに角の2等分線の方向に移動していることが確認できます.
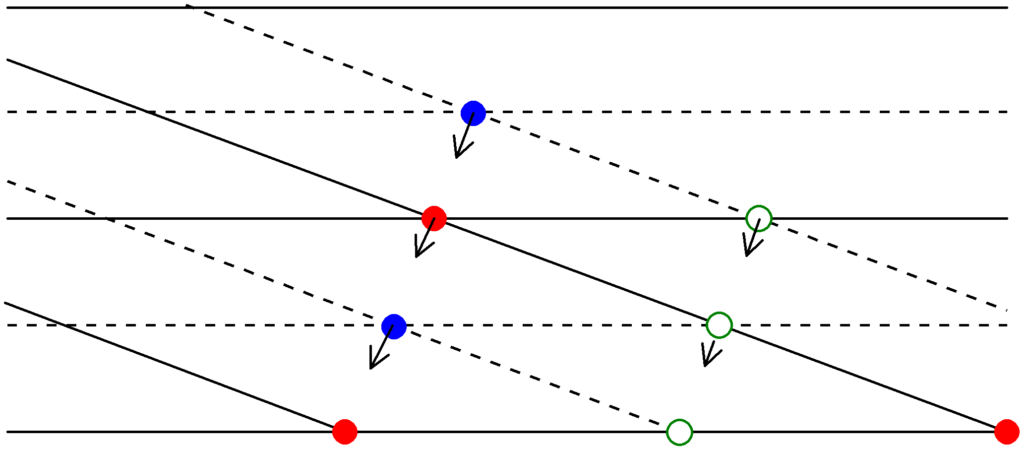

上図はある瞬間の平面波の様子を描いています.つまり,ただの写真です.
明線(腹の部分,つまり,大きく振動しているところ)を見つけるためには,その後波の動きをする必要があります.
実線はそれぞれの波面の山,点線が谷です.また,2つの波面が重なりあったときの合成波について,赤丸は山,青丸は谷,緑白丸は変位$0$の点です.それぞれの山,谷,変位$0$は矢印の方向に動きます.
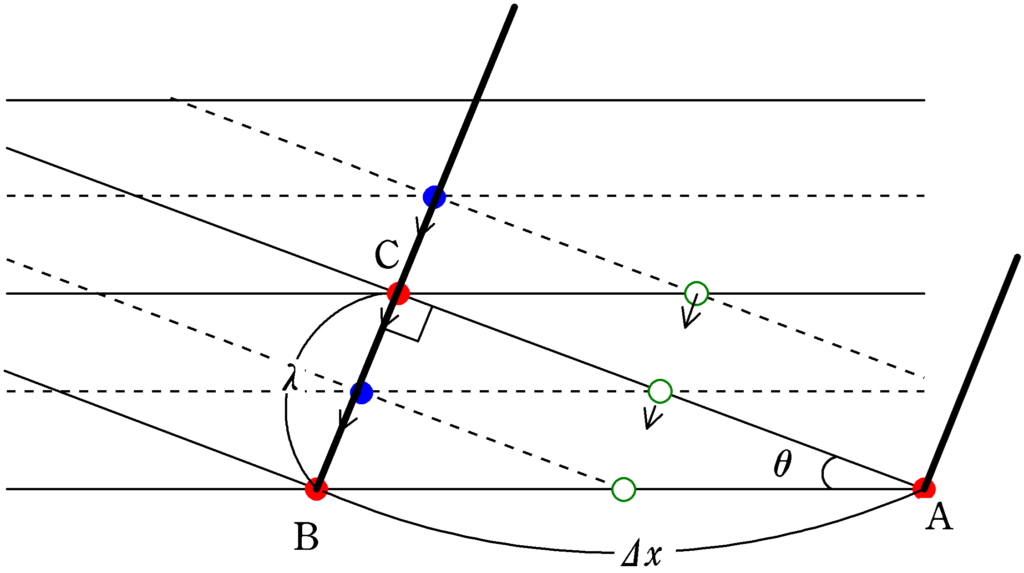

図のB点で観測すると,今現在は山ですが,いずれ青丸の谷がきて,さらに時間が経つと赤丸の山がきます.つまり,山と谷が交互にくるような大きな振動をすることになり,ここが明線が見える場所です.上図の太線は腹線です.A点を通る腹線との距離$\varDelta x$は直角三角形$\rm ABC$に着目して
$\sin\theta=\dfrac{\lambda}{\varDelta x}$ $\therefore\,\, \varDelta x=\dfrac{\lambda}{\sin\theta}$(答)
ちなみに,$\angle{\rm BAC}=\theta$の理由は「2つの直線のなす角とその法線同士のなす角が等しい」からです.
(2)
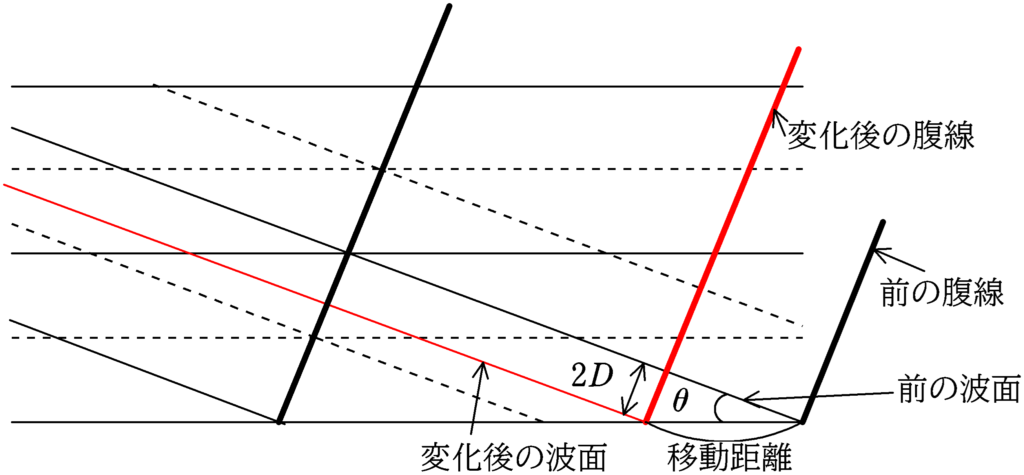

鏡を微小距離$D$だけ移動させると,その往復分$2D$だけ距離が縮むので,上図のように,経路Xが前の波面(黒の細実線)より,$2D$分だけ進んだ形(赤の細実線)になります.すると,波面と波面の交点にずれが生じ,その結果明線の位置もずれることになります.鏡Aを移動する前の腹線より,左方向に移動する(赤の太実線)ことが上図から確認できます.その移動距離は
$\sin\theta=\dfrac{2D}{移動距離}$ $\therefore\,\, 移動距離=\dfrac{2D}{\sin\theta}$
なので,移動が左方向だから,符号に注意して,$\varDelta X=-\dfrac{2D}{\sin\theta}$(答)




コメント