
磁石内の磁束線がどのようになっているかの問題です.
かなり簡略化した問題なので,もっとしっかりと解きたい方は「2000年早稲田理工」の問題を解くことをおすすめします.
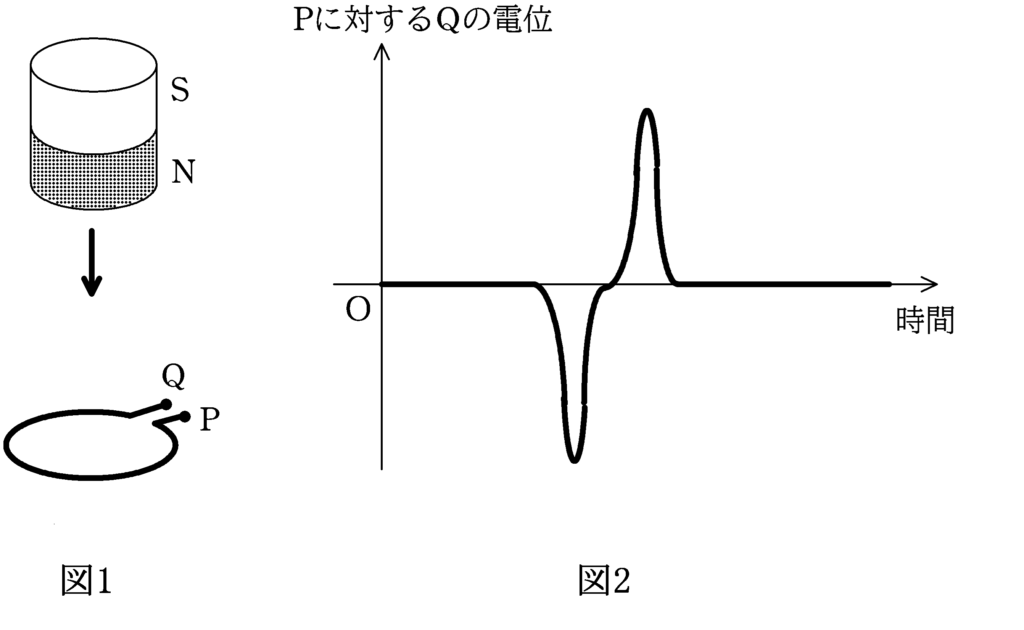
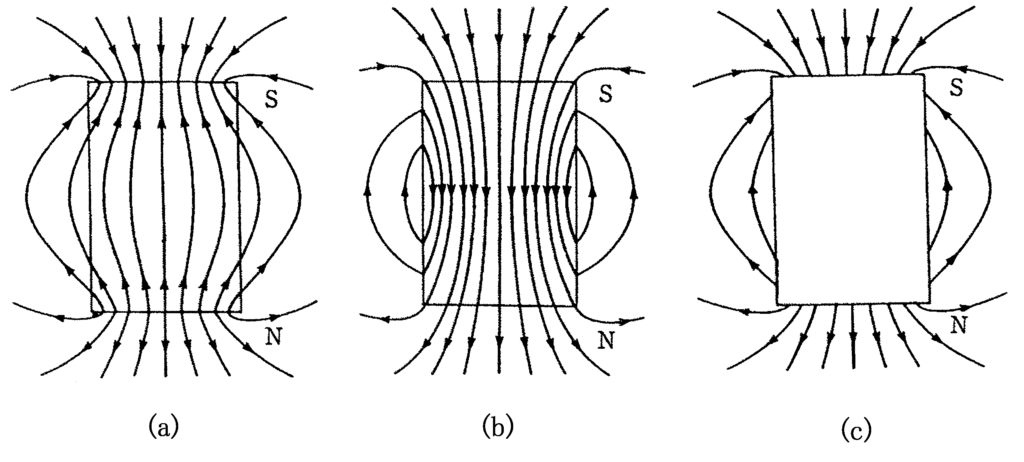
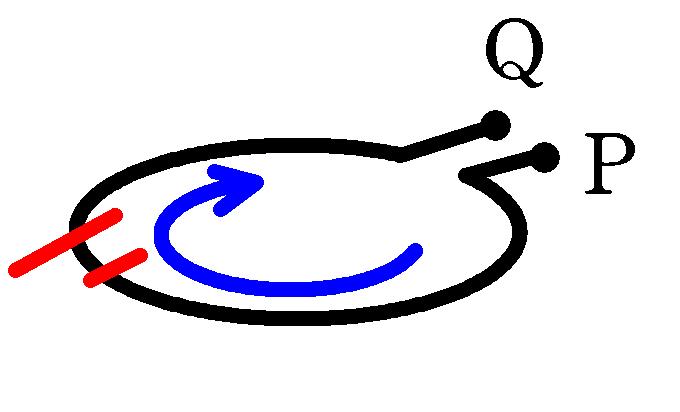
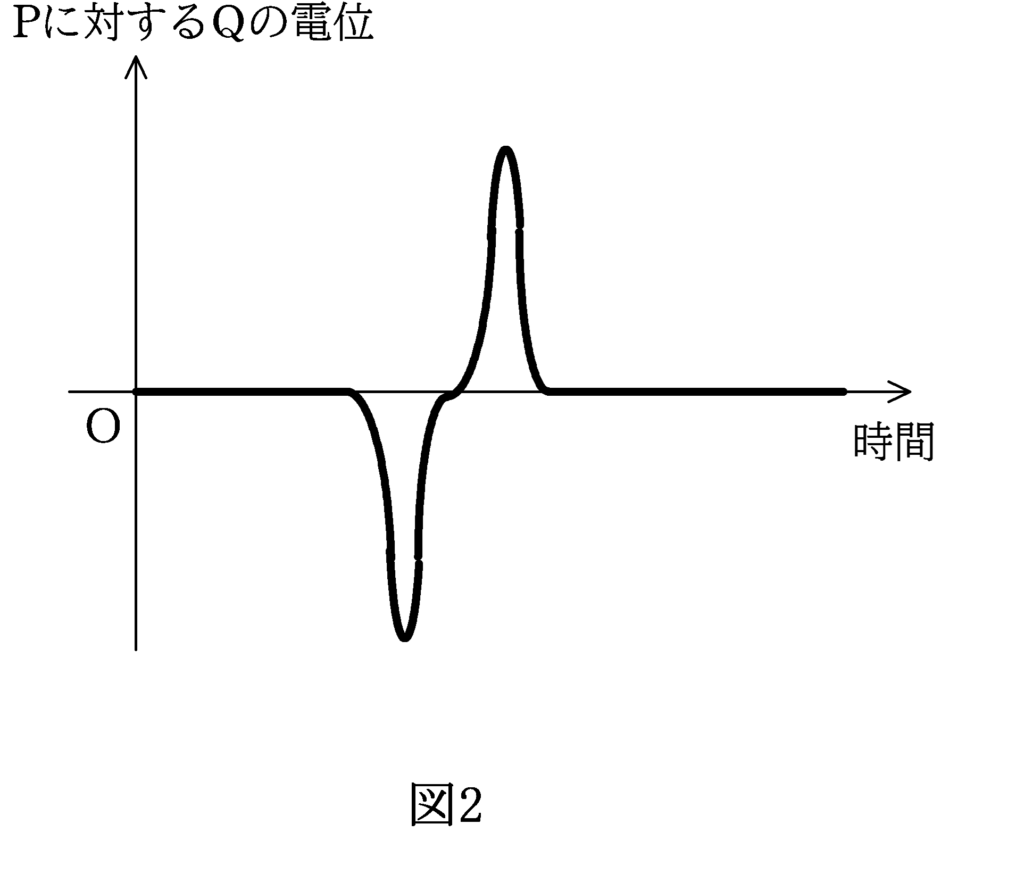
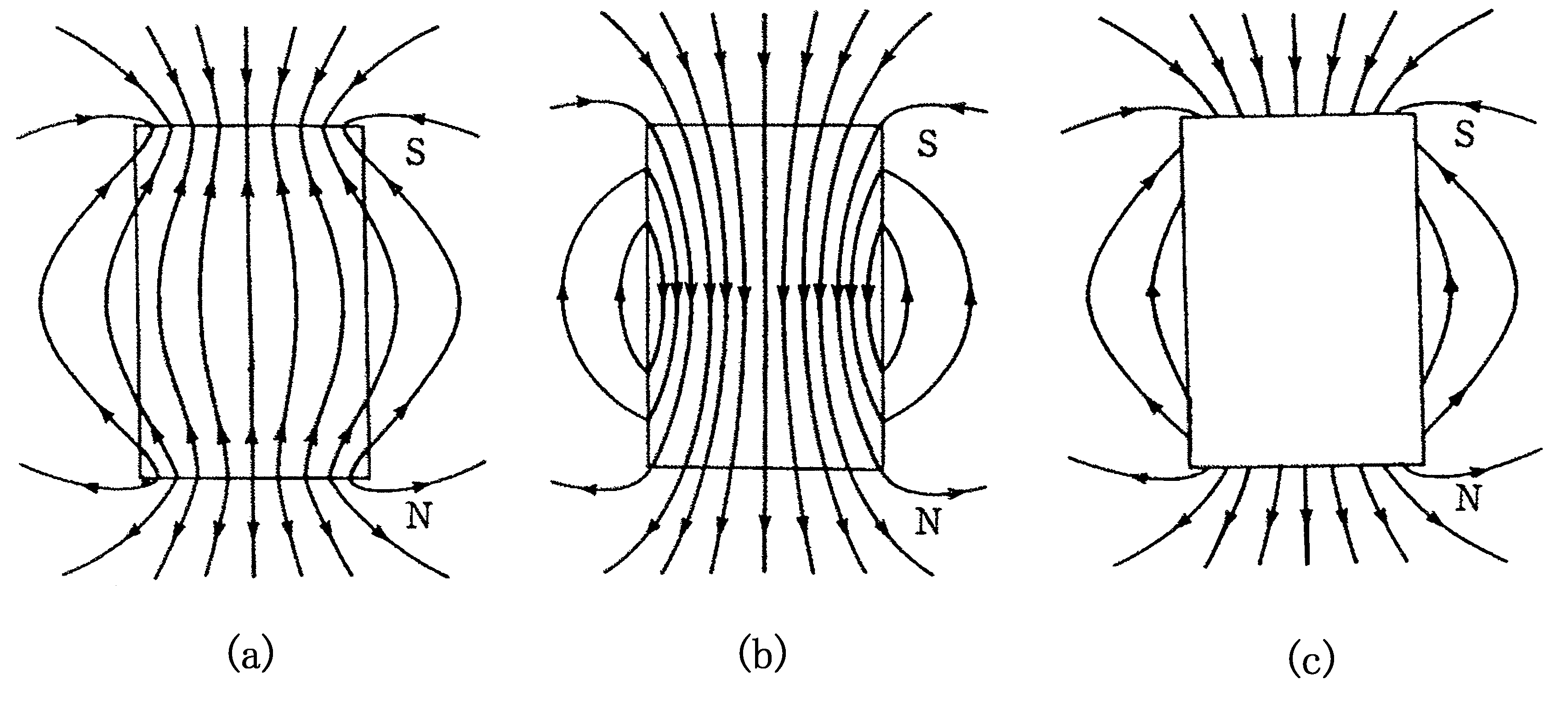
図1のように,軸を鉛直においたコイル中に磁石を落下させ,コイルの端Pに対するQの電位の時間変化を測定した結果,図2のようになった.磁石内の磁束の様子として最も適当なものを次の(a)~(c)の選択肢の中から一つ選べ.
<解答>
コイル内の磁束が変化すると誘導起電力が生じます.その誘導起電力の大きさは次のように計算できます.
$\varDelta t$の間に磁束が$\varDelta \varPhi$変化するときに生じる誘導起電力の大きさ$V$は
$V=|\dfrac{\varDelta \varPhi}{\varDelta t}|$
また,起電力の向きは次のレンツの法則で決まります.
磁束をもとにもどす方向に右手親指を向け,残りの4本指の方向の方向に起電力が生じる.
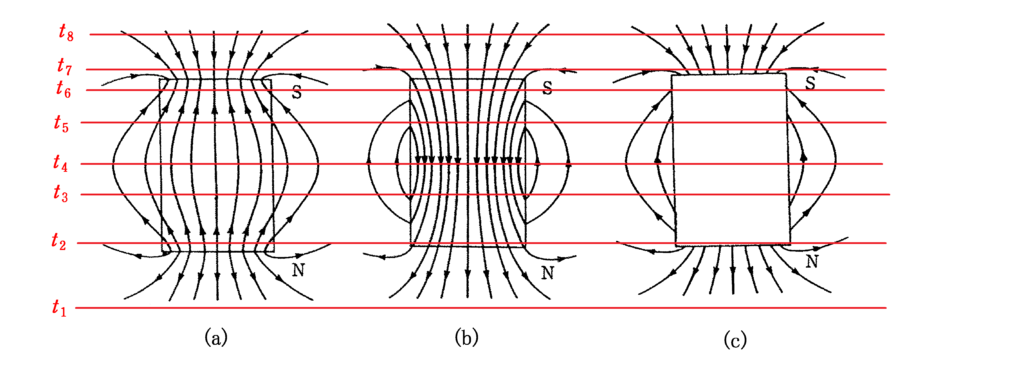
時刻$t=t_{1}$のときの磁石とコイル($t=t_{1}$と書かれている右の赤線の場所にコイルがある)の位置関係のときは(a),(b),(c)ともに下向きの磁束が増えていくので,もとの磁束にもどすように右手親指を上向きに向けると,残り4本指は下図のように鉛直上向きからみると反時計回りを向きます.
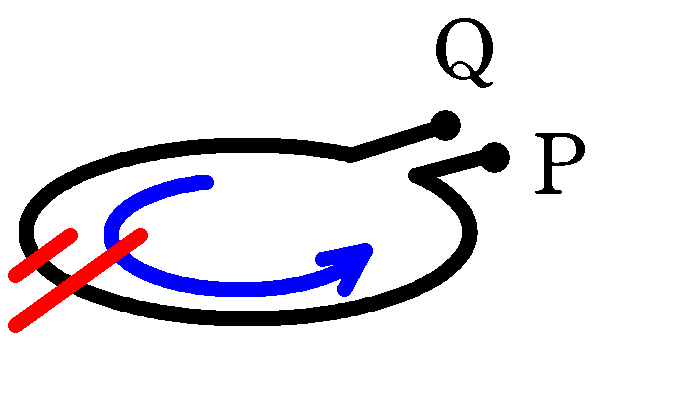
するとPに対するQの電位は負となり,これは(a)~(c)すべて同じなので区別がつきません.

時刻$t=t_{2}$のときの磁石とコイル($t=t_{2}$と書かれている右の赤線の場所にコイルがある)の位置関係のときは(a)はもともと下向きの磁束であったものが急に上向きの磁束がコイルを貫くため,もとの磁束にもどすように右手親指を下向きに向けると,下図のようにPに対するQの電位が正になります.
これは(c)も同じで,もともと下向きの磁束があったものが急に磁束が0になるので,右手親指を下向きに向けることでPに対するQの電位が正になります.
一方,(b)はそこまで磁束が変化していないので(少しは変化しますが),少なくとも急に電位が正になることはないでしょう.

時刻$t=t_{3}$~$t_{6}$までは(a)~(c)すべてゆるやかな変化となので,誘導起電力も$0$付近となるでしょう.(正確にいうと(c)は変化なしで,(a)は上向きの磁束が減っていって(電位が負),ほぼ一定となり,その後に増えます(電位が正).そして,(b)は下向きの磁束が増えていって(電位が負),一定(電位0)となり,その後減って(電位が正)いきます.早稲田理工の問題はここらへんの違いも含めて考察するような問題になっています.)
$t=t_{7}$では,(a)はもともと上向きの磁束だったものが急に下向きの磁束を貫くので右手親指を上向きに向けると下図のように,Pに対するQの電位が負になります.

これは(c)も同じで,もともと磁束がない状態から,急に下向きの磁束が増えるので,Pに対するQの電位は負になります.
一方(b)は$t=t_{6}$のときと比べればそこまで磁束は大きく変化しません.なので,誘導起電力も$0$付近でしょう.

さいごに$t=t_{8}$ですが,(a)から(c)すべて下向きの磁束が小さくなっていくので,右手親指を下に向けると下図のようにPに対するQの電位は正になります.

ここまでの考察から
(a)は電位が
負→正→0付近→負→正
(b)は電位が
負→0付近→正
(c)は
負→正→0付近→負→正
となっています.
この中で一番図2に近いのは(b)と予想できます.(答)
ちなみに(a)は磁力線の図になっています.なんで$B=\mu H$なのに,磁力線と磁束線が違うの?と思うかもしれません.実は,磁石内のように磁化されているような場所では,$B=\mu H+J$と磁化$J$を加える必要があります.普段は$J=0$なので,$B=\mu H$で磁束密度と磁場がほぼ同じように見えるのです.



コメント