[ヤングの実験とは全然違う！？]単スリット

今回は単スリットについて説明をします．2スリットはヤングの実験でよく知られていると思います．2つのスリットを通る光が干渉し，スクリーンに明線と暗線を交互に作ります．一方，単スリットは1つのスリットを通る無数の光が干渉し，明線と暗線を作ります．干渉条件に違いがあるので，注意をしましょう．

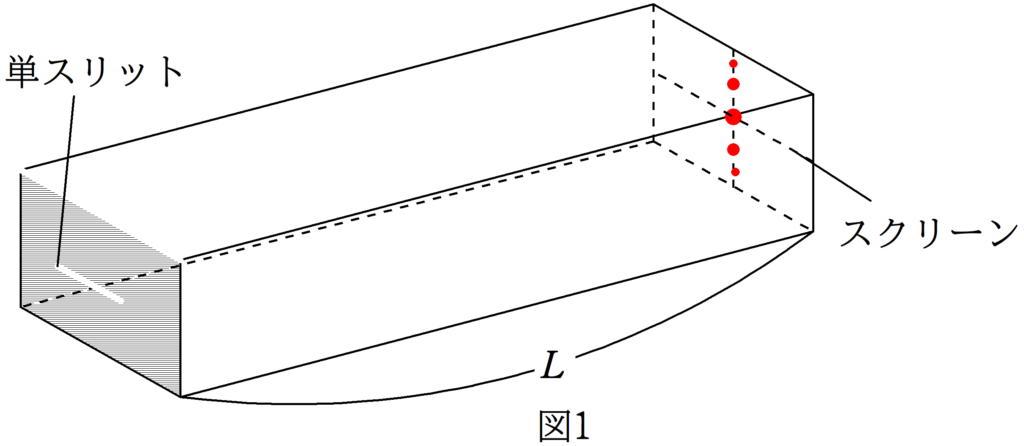
　単スリットの明線条件，暗線条件

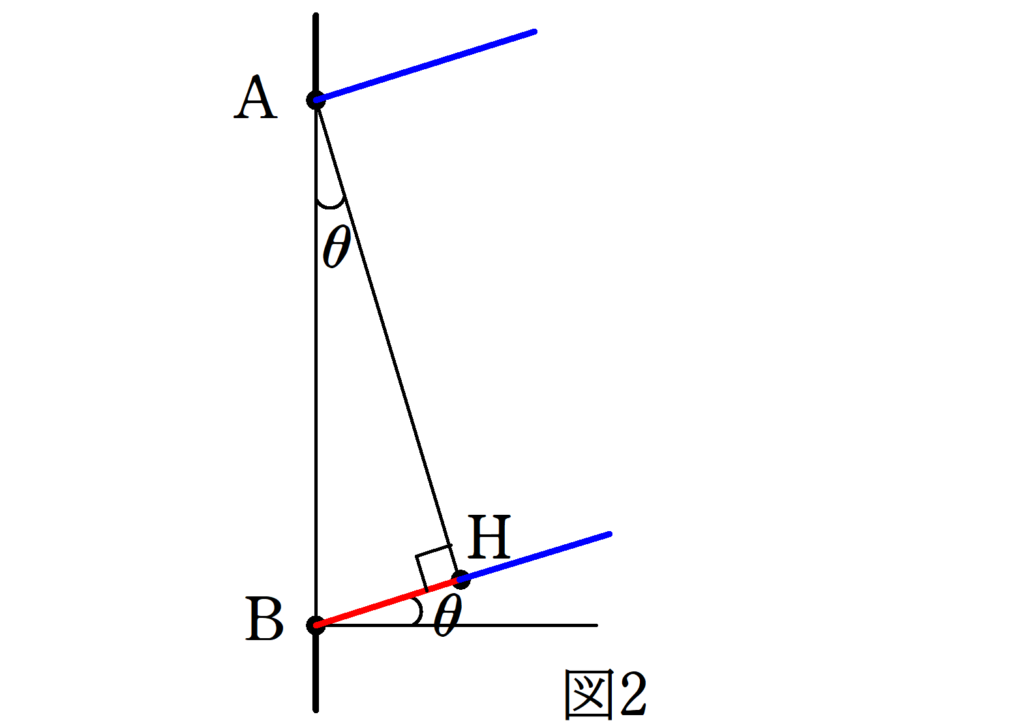
図2において，スリットの幅を$D$としてAからスクリーンの方向にいく光（青の方向）と，Bからスクリーンの方向にいく光を考えます．このとき，AからBの光線の方向の直線へ下した垂線の足をHとし，AとBの光線の方向を$\theta$とします．このとき，

$\rm{BH}$$=D\sin \theta$

となることが確認できます．光の波長を$\lambda$，整数$m$を使えば，明線条件と暗線条件は次のようになります．

明線条件$\left\lbrace \matrix{ D \sin \theta =0 \dots 明るい　\cr D\sin \theta =(m+\dfrac{1}{2})\lambda \dots やや明るい }\right\rbrace $

暗線条件$\{D\sin \theta =m\lambda (m\neq 0) \dots暗い　\}$

見た目はヤングの実験と真反対のように見えますが，物理法則が違うというわけではありません．なぜ，上のような干渉条件になるのかを考えてみましょう．

　$D\sin \theta =0$

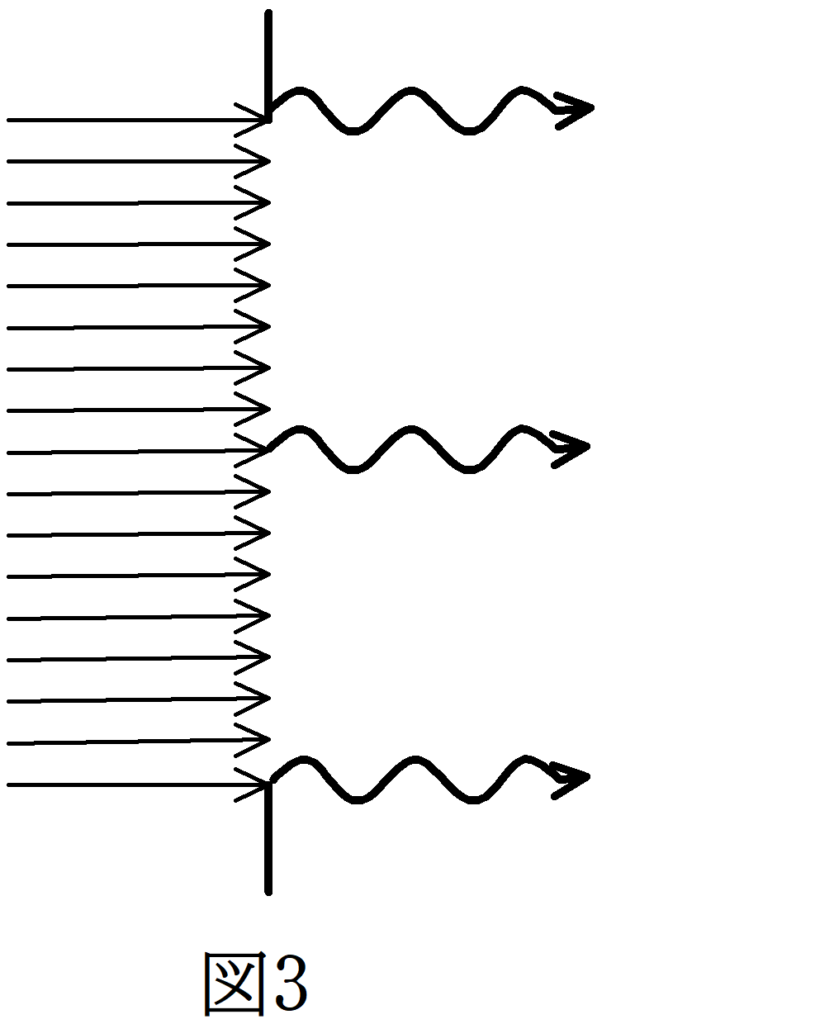
$D\sin \theta =0$のとき，すべての光の振動は同じタイミングであるから，スクリーンでの振幅が大きくなります．そのため，単スリットの真正面にある場所では明るい線が見えます．

　$D\sin \theta =\lambda$

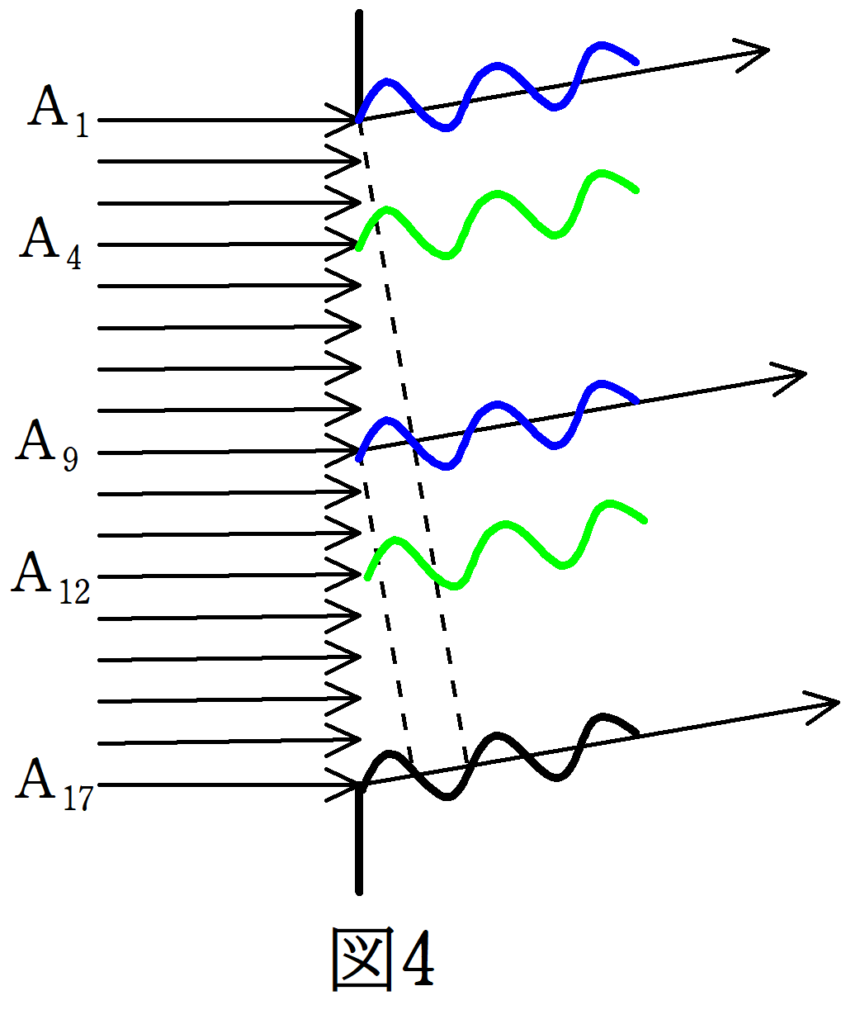
図4では便宜的に17本の光線を考えてみました．上の光線から番号をふって$\rm{A_{1} , A_{2} , \dots , A_{17}}$とします．$D\sin \theta =\lambda$であるから，$\rm{A_{1}}$からスクリーンまでの距離と$\rm{A_{17}}$からスクリーンまでの距離は$\lambda$の差があります．すると，$\rm{A_{1}}$と$\rm{A_{9}}$はちょうど真反対の振動となり，スクリーンにおいて振動が打ち消す形となります．振動を打ち消すのはこれだけではありません．$\rm{A_{4}}$と$\rm{A_{12}}$も打ち消します．このように，必ず真反対の振動のものが存在し，同様に，$\rm{A_{2}}$と$\rm{A_{10}}$ ，$ \dots $，$\rm{A_{8}}$と$\rm{A_{16}}$が打ち消し合います．唯一この図では$\rm{A_{17}}$だけ残ることになりますが，ほぼすべてが打ち消すので，スクリーンでは暗くうつります．

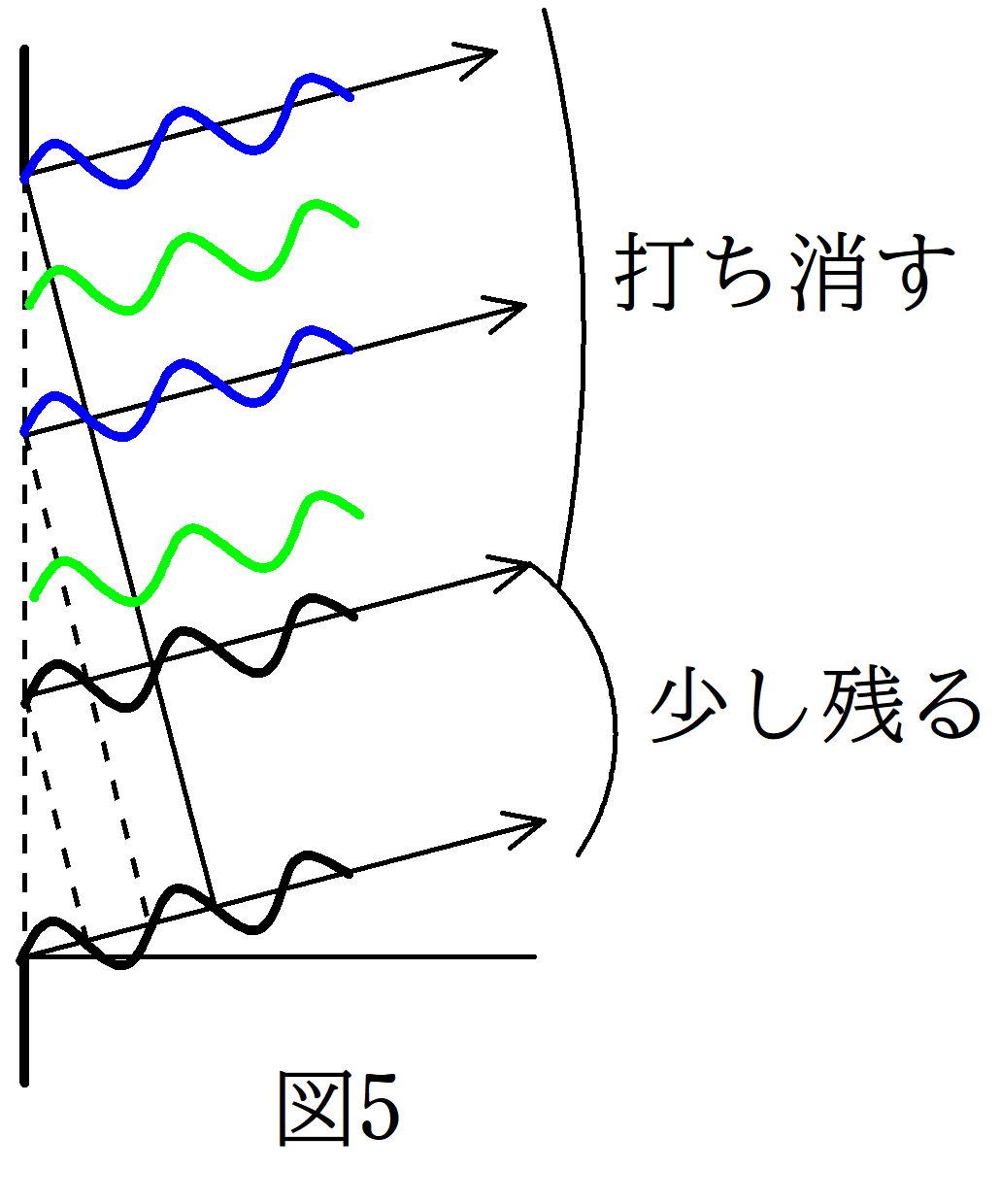
　$D\sin \theta=\dfrac{3}{2}\lambda$

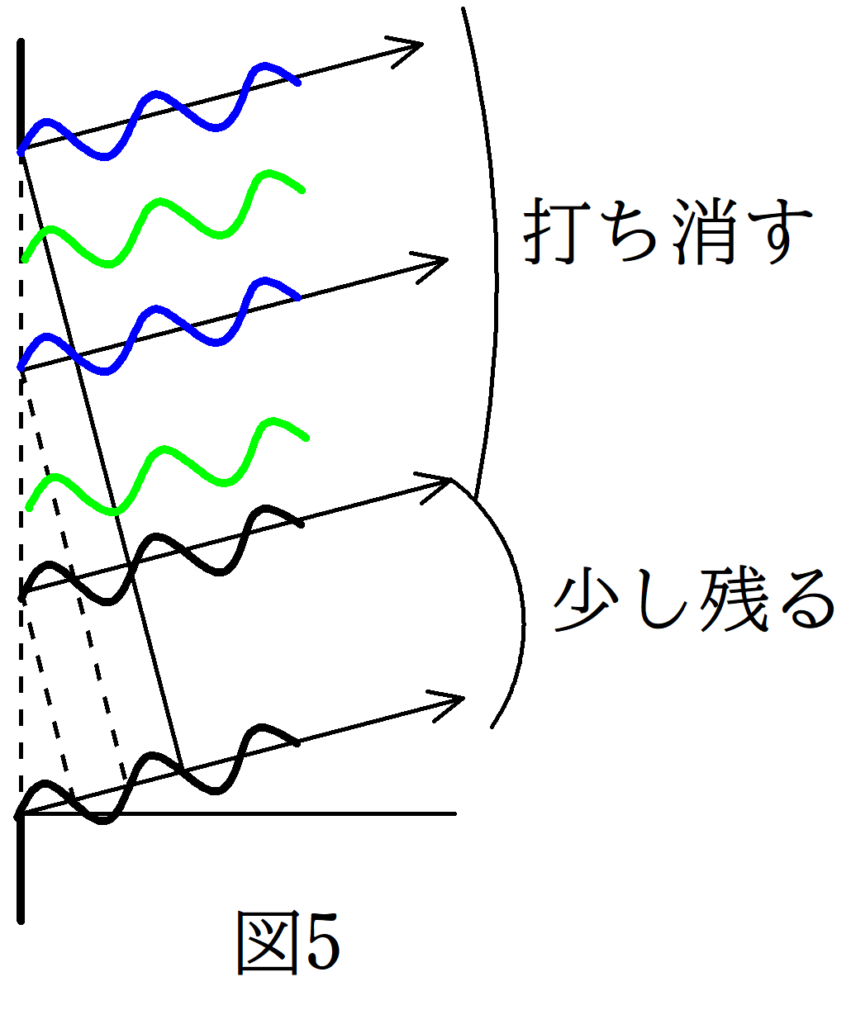
今度は，$D\sin \theta=\dfrac{3}{2}\lambda$であるから，一番上の光線と一番下の光線は$\dfrac{3}{2}\lambda$の差があります．ということは，図4と同じように一番上の光線との距離の差が$\lambda$の場所もありますし，$\dfrac{1}{2}\lambda$のところもあります．上図のように青と青の光線は打ち消し，緑と緑も打ち消し，大部分は打ち消すこととなります．しかし，距離の差が$\dfrac{1}{2}\lambda$以下の下部分では打ち消す相手が見つからず少し残ります．この方向にできるのは$D\sin \theta=0$ほど明るくはありませんが，それでもやや明るく見えるはずです．

　$D\sin \theta =2\lambda$

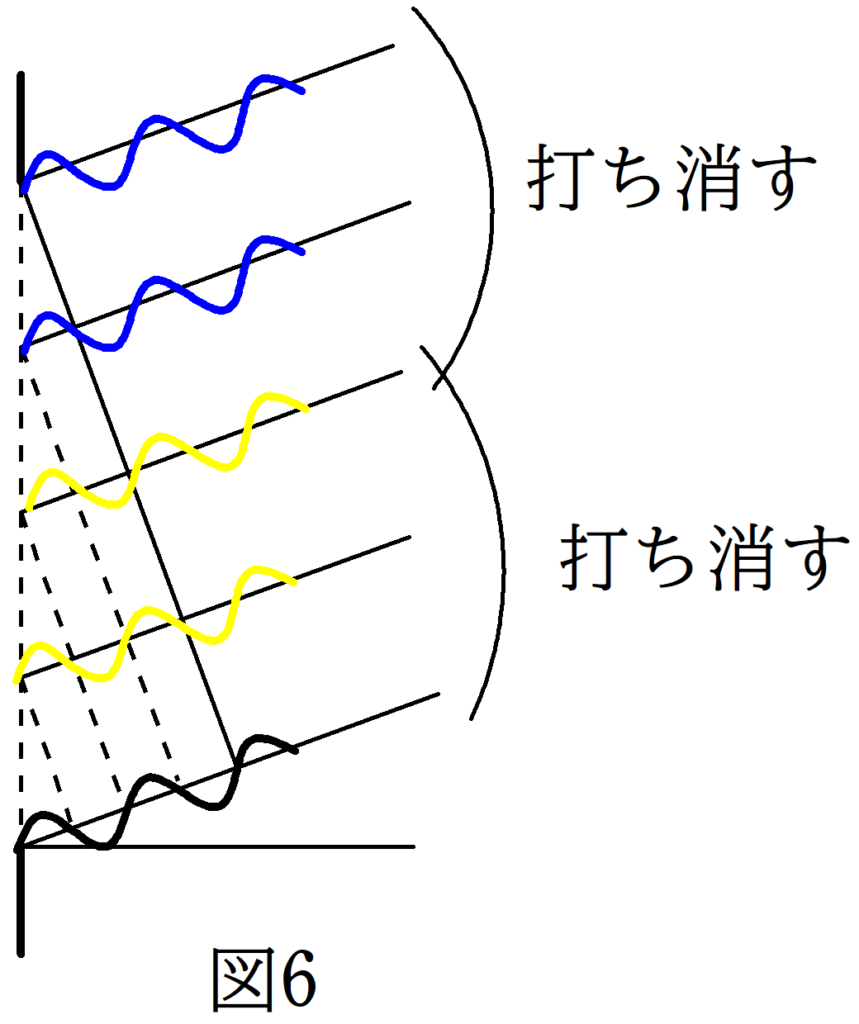
図6では，図4と同様に，ほぼすべての光が打ち消し合います．図6では青と青，黄色と黄色が打ち消し合います．結局この方向は暗くなるでしょう．

　$D\sin \theta =\dfrac{5}{2}\lambda$

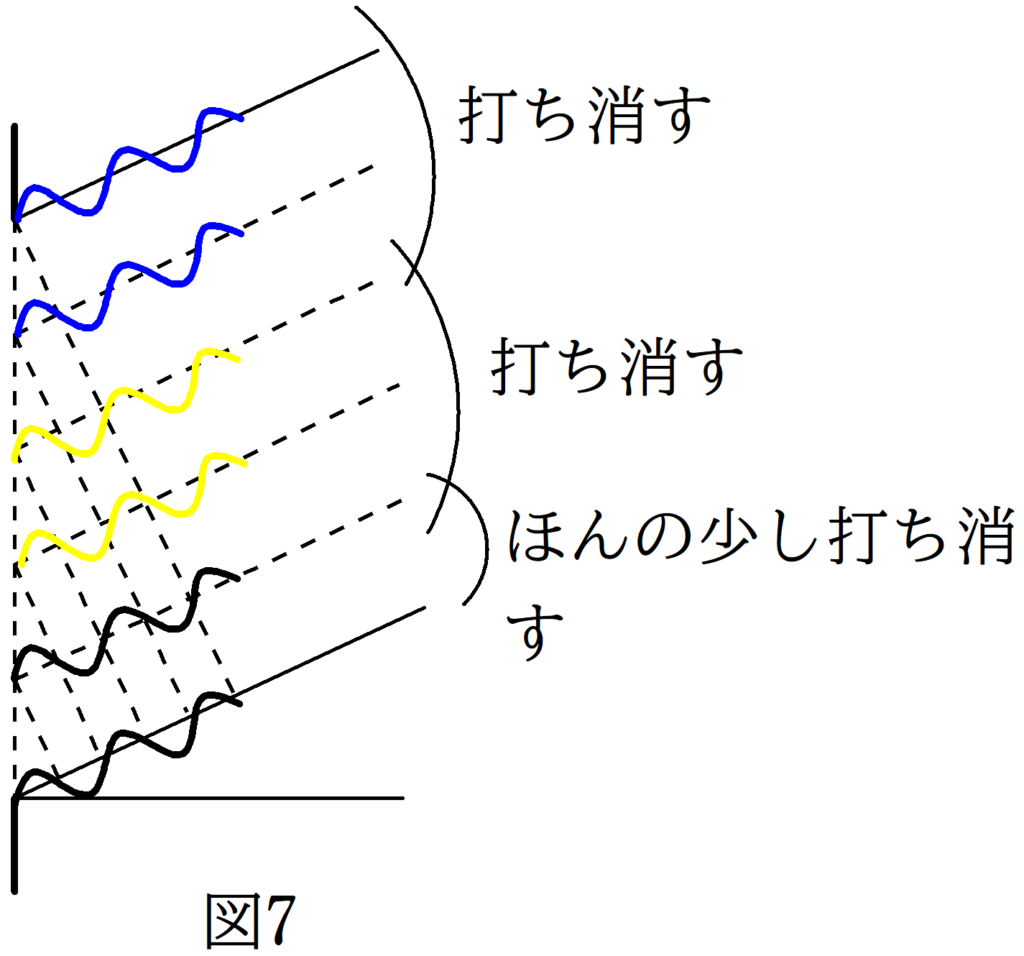
さらに，角度が傾いていくと，打ち消す部分が多くなっていきます．なので，まわりよりは明るいのですが，やや明るい程度でしょう．

　まとめ

単スリットの問題では，ヤングの実験のように2つの光線だけのタイミングを考えるのではなく，単スリットを通る無数の光線のタイミングをかんがえていきます．したがって，ある光線の振動と他の振動のタイミングが真反対で，打ち消してしまうものもたくさんあります．このとき，すべて打ち消してしまえば，暗くなるし，少しでもうち消さないものが残れば明るくなります．

今まで考えてきたように，単スリットの真正面は明るく，その後，真正面の部分から離れると，暗い→明るい→暗い，を繰り返しますが，同じ明線でも真正面から距離が離れるほど薄暗くなっていきます．

実はヤングの実験でも同じような効果が起こります．真正面からの距離が離れるほど明線が暗くなっていきます．これは，単スリットの効果で，各スリットで単スリットの干渉を起こしているからです．（実際の入試問題では，この単スリットの効果を無視する問題もあるので，よく問題文を読みましょう．）