
今回は重心の問題です!早速解いてみましょう.
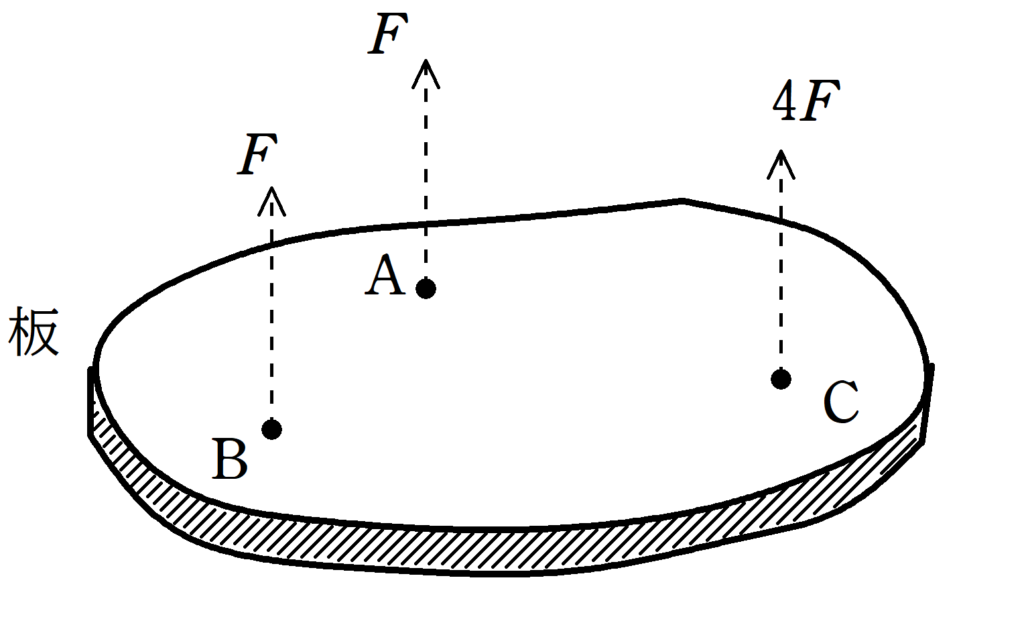
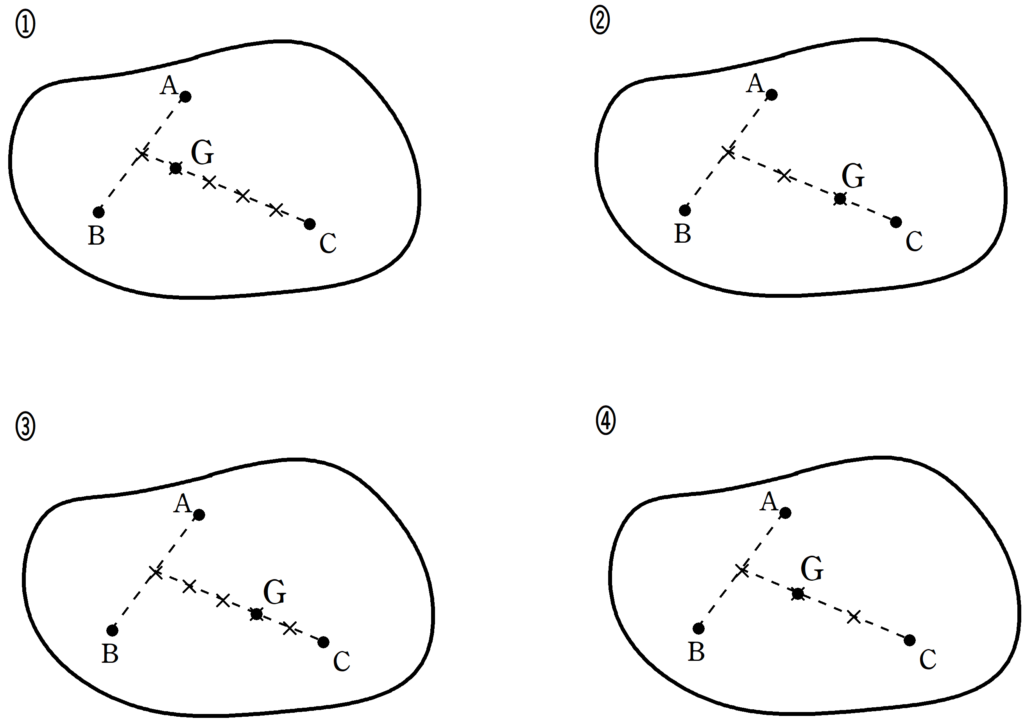
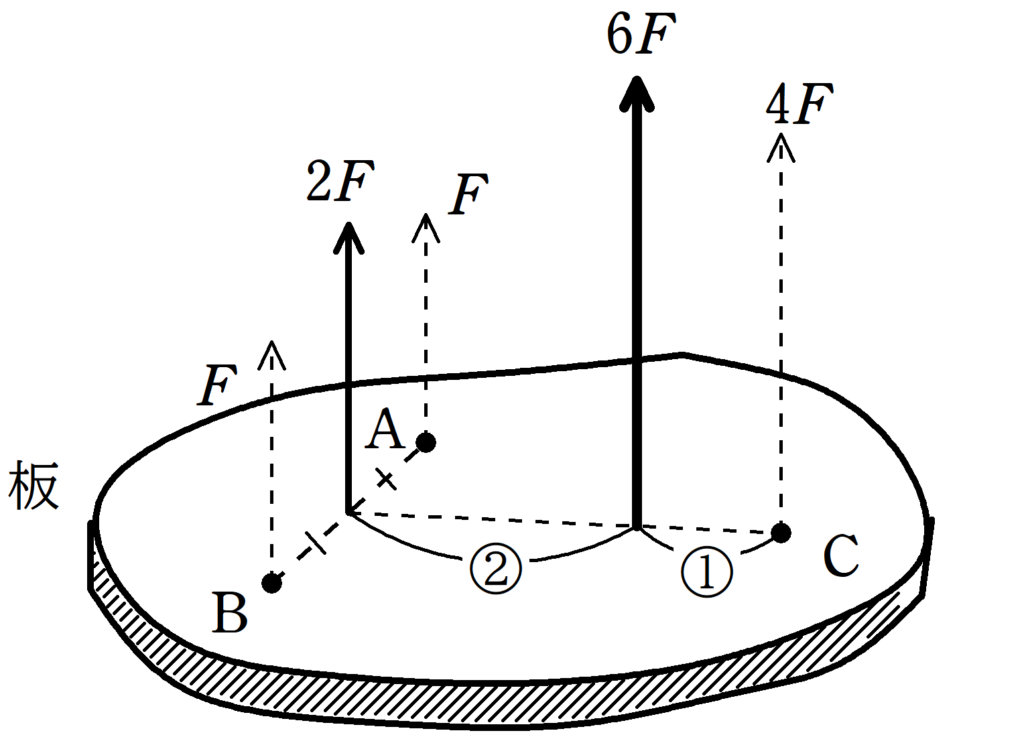
下図のような板がある.板上のA , B , Cの場所にそれぞれ力の大きさ$F , F , 4F$の力を鉛直方向に加えて支えたところ,板は水平につりさげられた.板の重心Gとして最も適当なものを次の①~④の中から選べ.

では,重心は何か?から復習しましょう.
重心とは
質量$m_{1}$の物体Aと質量$m_{2}$の物体Bがそれぞれ,$x_{1}$,$x_{2}$の場所にあります.
このとき,AとBの重心$x_{\rm{G}}$は次のように定義されています.
$x_{\rm{G}}=\dfrac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}$
重心のまわりの重力のモーメントはつり合います.
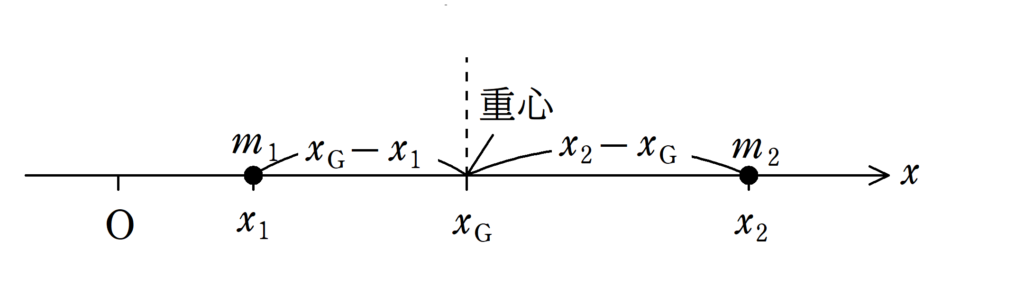
重心を力のモーメントの中心とすると,Aの方が反時計回りの力のモーメントで大きさが$(x_{\rm{G}}-x_{1})m_{1}g$,Bの方が時計回りの力のモーメントで大きさが$(x_{2}-x_{\rm{G}})m_{2}g$なので
$\eqalign{(x_{\rm{G}}-x_{1})m_{1}g&=(x_{2}-x_{\rm{G}})m_{2}g\cr x_{\rm{G}}&=\dfrac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}}$

多数の質量があるときは,
重心に物体の全質量が集まったと考えていいです!
同じ向きの平行力の合成
同じ向きで平行な力は合成することができます.

上図のように,A点とB点にそれぞれ平行で同じ向きに,大きさ$F_{1}$と$F_{2}$の力がかかっているとします.このとき,A点にはたらく力とB点にはたらく力を合成すると
- 向き→2つの力と同じ向き
- 大きさ$F_{1}+F_{2}$
- 合力の始点→ABを$F_{2}:F_{1}$に内分した点P(つまり,2力の逆比)

PはAにはたらく力とBがはたらく力のモーメントがつり合う場所でもあるね!
解答

これで準備が整いました.
まず,板の全質量は重心にあると考えてよいです.
そして,板がつり合っているということは,A点,B点,C点にはたらく平行力の合力が重心と同じ場所で逆向きにかかっているということですね.それでは,問題を解きましょう.
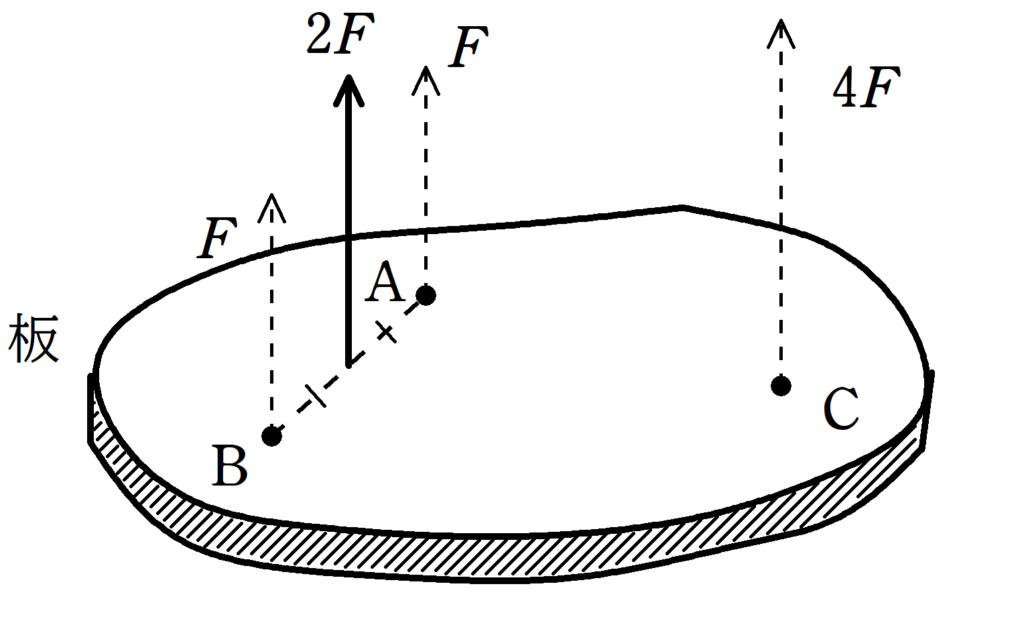
まず,AとBにはたらく平行力を合成します.どちらも同じ大きさの力なので,AとBの中点に合力がはたらきます.合力の大きさは$2F$です.
次にAとBの平行力の合力とCにはたらく力を合成します.力の大きさの比が$2:4=1:2$なのでAとBの中点とCを$2:1$に内分する場所に力の合力がはたらきます.
板が水平につり下げられた,ということからA , B , Cにはたらく力の合力と重心にはたらく重力が同じ場所にはたらき向きが逆で,同じ大きさであるということがわかります.

ということで,答えは②です!
なんとなくできた!という人も,どのように考えればいいのかをもう一度整理しておきましょう!




コメント