
プリズムの問題はできなくはないけど,時間がかかる!という人はいませんか?
次の問題を通して,次の2つを復習しましょう.
1. 屈折の法則
2. プリズムの問題で着目する3つのこと.
下図のように,屈折率$n$の媒質でつくられた頂角$\alpha$のプリズムが置かれている.今,プリズムに単色光を当てる.単色光はA点を入射し,プリズム中を進む.その後,B点を通り抜ける.A点での入射角と屈折角をそれぞれ$\theta_{1}$,$\theta_{1}^{\prime}$,B点での入射角と屈折角をそれぞれ$\theta_{2}^{\prime}$,$\theta_{2}$とする.
A点から入射される光線とB点から出る光線のなす角(偏角)を$\delta$とする.また,プリズムは空気中におかれており,空気の屈折率を1とみなす.以下の問いに答えよ.
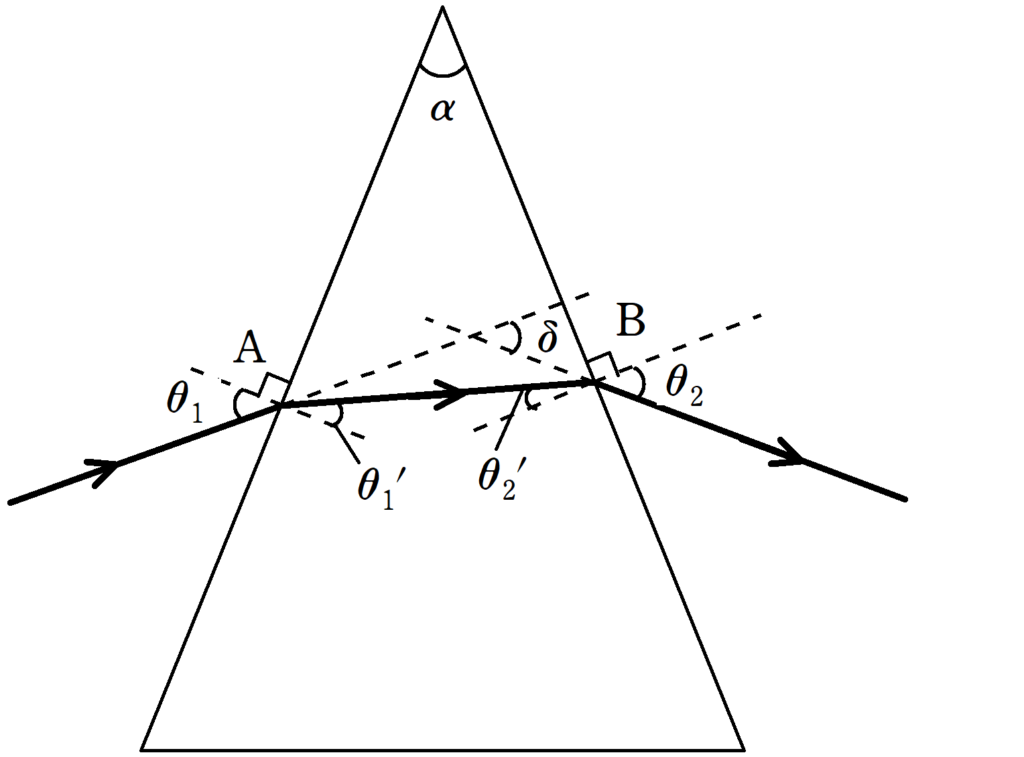
(1) A点における屈折の法則を表す式として,適当なものを次の中から選べ.
$① \sin \theta_{1}=n\cos \theta_{1}^{\prime}$ $② n\sin \theta_{1}=\cos \theta_{1}^{\prime}$
$③ \cos \theta_{1}=n\cos \theta_{1}^{\prime}$ $④ n\cos \theta_{1}=\cos \theta_{1}^{\prime}$
$⑤ \sin \theta_{1}=n\sin \theta_{1}^{\prime}$ $⑥ n\sin \theta_{1}=\sin \theta_{1}^{\prime}$
(2) 偏角$\delta$を表したものとして正しいものを次の中から選べ.
$① \delta=\theta_{1}+\theta_{2}+\alpha$ $② \delta=\theta_{1}-\theta_{2}-\alpha$
$③ \delta=\theta_{1}+\theta_{2}-\alpha$ $④ \delta=\alpha-\theta_{1}-\theta_{2}$
$⑤ \delta=\alpha-\theta_{1}+\theta_{2}$ $⑥ \delta=\alpha+\theta_{1}-\theta_{2}$

解答は一番最後にあるからチェックしてみてくださいね!
それでは,まず,屈折の法則から復習します.
屈折の法則

屈折の法則は,間違うポイントがたくさんあるから,しっかりと整理しておきましょう.
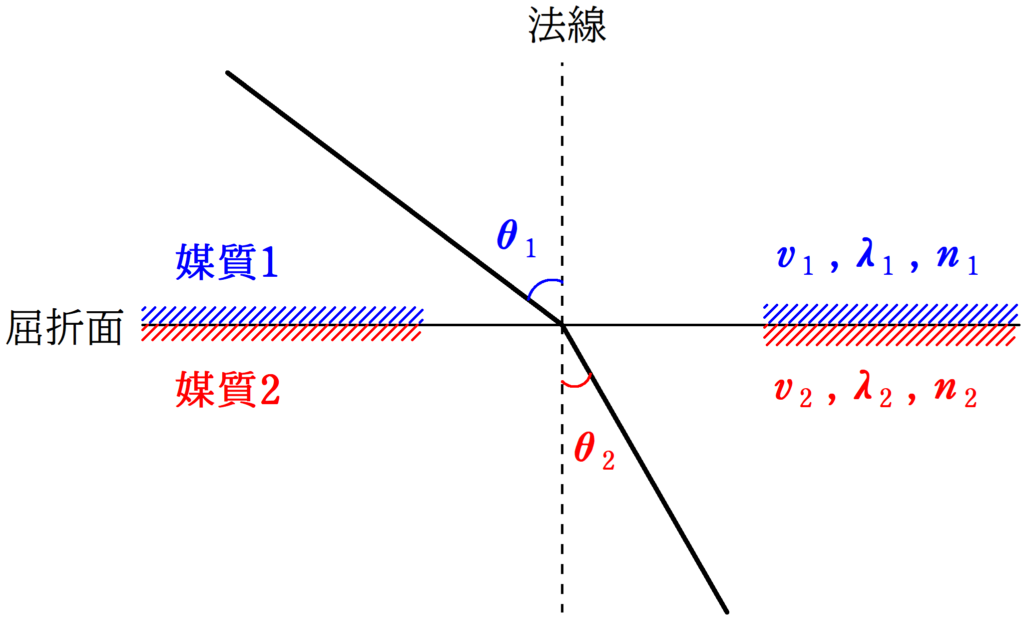
光が媒質1に入射し,媒質2へ屈折することを考える.
媒質1の入射角を$\theta_{1}$,波が伝わる速さを$v_{1}$,波長を$\lambda_{1}$,絶対屈折率を$n_{1}$とする.また,媒質2の入射角を$\theta_{2}$,波が伝わる速さを$v_{2}$,波長を$\lambda_{2}$,絶対屈折率を$n_{2}$とする.このとき,次の関係が成り立つ.
$\dfrac{\sin \theta_{1}}{\sin \theta_{2}}=\dfrac{v_{1}}{v_{2}}=\dfrac{\lambda_{1}}{\lambda_{2}}=\dfrac{n_{2}}{n_{1}}$

よくある間違いは次の3つです...
- $\dfrac{\sin \theta_{1}}{\sin \theta_{2}}$ではなく,$\dfrac{\theta_{1}}{\theta_{2}}$としてしまう.(近似できるときはこの形もあるんですが..)
- 屈折によって,振動数や周期まで変化すると勘違い.実際は屈折によって,振動数や周期は変化しません!
- $\dfrac{\sin \theta_{1}}{\sin \theta_{2}}=\dfrac{v_{1}}{v_{2}}=\dfrac{\lambda_{1}}{\lambda_{2}}=\dfrac{n_{1}}{n_{2}}$と覚えている.つまり,屈折率の分母と分子を逆にして覚えている.
特に,3はとても間違いやすいので,次のように覚えておくとよいでしょう.
$n_{1}\sin \theta_{1}=n_{2}\sin \theta_{2}$
$n_{1}v_{1}=n_{2}v_{2}$
$n_{1}\lambda_{1}=n_{2}\lambda_{2}$

あと,もう1つ!
中学生の頃も同じ間違いをしたかもしれませんが,入射角や屈折角は屈折面に垂直な線,つまり法線からのなす角です!屈折面からのなす角ではありません!
(1)の解答
問題では,法線からのなす角がとられているので,安心して屈折の法則を立てましょう.空気の屈折率が$1$,プリズムの屈折率が$n$なので,屈折の法則より
$1\cdot \sin \theta_{1}=n\cdot \sin \theta_{1}^{\prime} $
つまり,⑤が正解です.
プリズムの問題で着目する3つのこと

プリズムの問題では次の3つのことに気づかないといけません.
① 4点が同一円周上にあることに気づく.
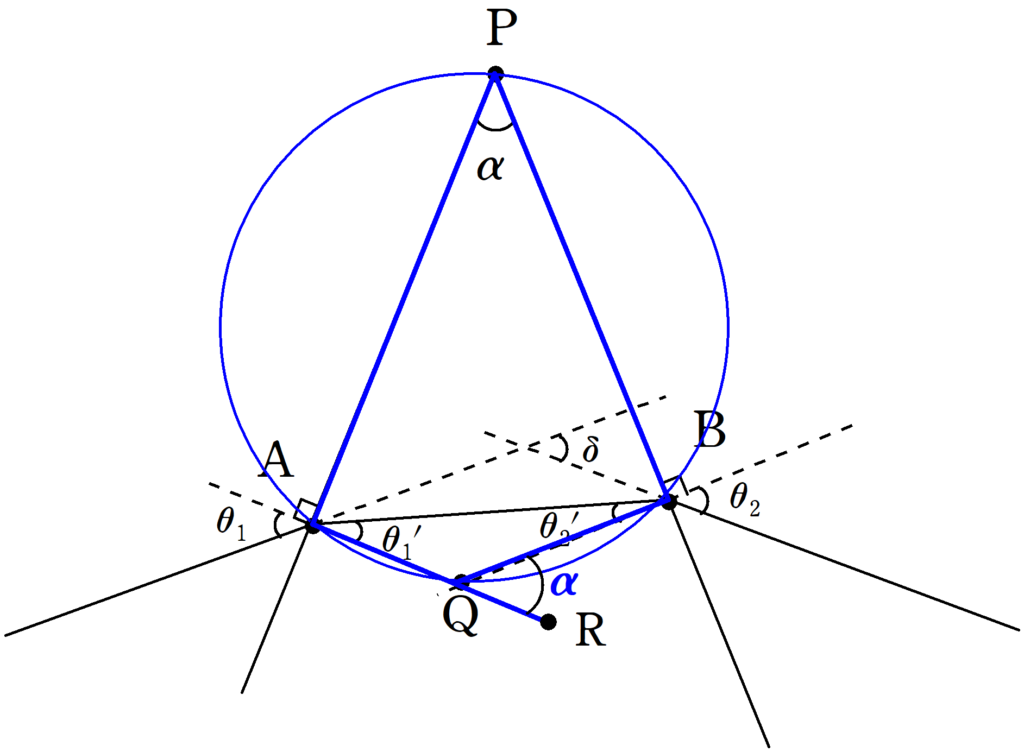
上図のAは入射する点,Bは屈折する点,Pはプリズムの頂点,QはAを通る法線とBを通る法線との交点です.このとき
PAQBは同一円周上にある
ことに気づきましょう.同一円周上にある理由は簡単です.$\angle \rm{PAQ}=\angle \rm{PBQ}=90°$だからです.円周角の定理の逆ですね.
すると,AQの延長線上のQ側の一点をRとして,円に内接する四角形の対角の和が$180°$であることから,次のことが成り立ちます.
$\angle \rm{APB}=\angle \rm{BQR}$
つまり,
$\angle \rm{BQR}=\alpha$
です.
② 外角と内角の和の関係1
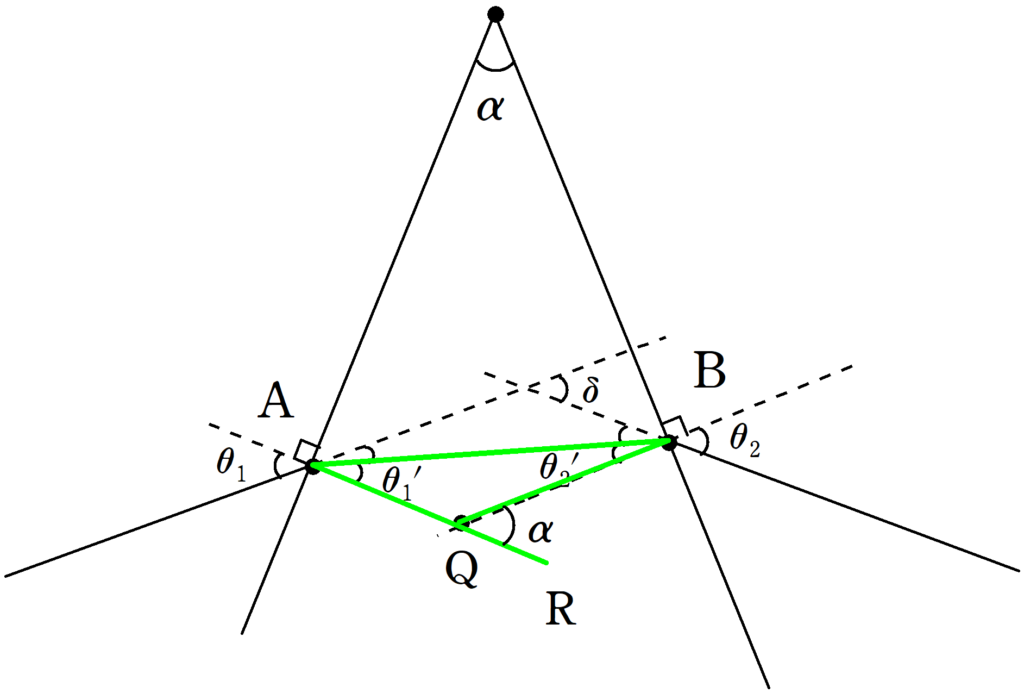
次に上図の緑色の三角形に着目します.三角形の外角と内角の和の関係より
$\alpha =\theta_{1}^{\prime}+\theta_{2}^{\prime}$ $\cdots (\ast)$
の関係が成り立ちます.
③ 外角と内角の和の関係2
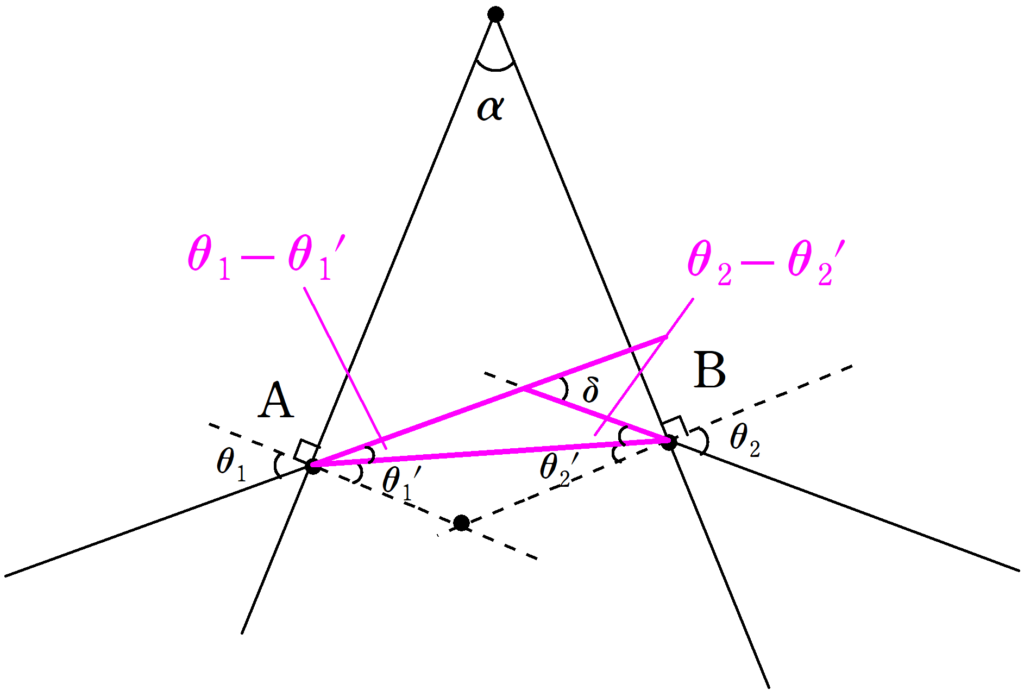
次にピンクの三角形の外角と内角の関係を考えましょう.
$\delta =(\theta_{1}-\theta_{1}^{\prime})+(\theta_{2}-\theta_{2}^{\prime})$ $\cdots (2\ast)$
(2)の解答
$\alpha =\theta_{1}^{\prime}+\theta_{2}^{\prime}$ $\cdots (\ast)$
$\delta =(\theta_{1}-\theta_{1}^{\prime})+(\theta_{2}-\theta_{2}^{\prime})$ $\cdots (2\ast)$
より,$\theta_{1}^{\prime}$と$\theta_{2}^{\prime}$を消去しましょう.$(2\ast)$より
$\eqalign{\delta &=\theta_{1}+\theta_{2}-(\theta_{1}^{\prime}+\theta_{2}^{\prime})\\&=\theta_{1}+\theta_{2}-\alpha}$
したがって,(2)の答えは③です.
問題の解答
(1) ⑤ (2) ③

今回は屈折の法則とプリズムの偏角の問題でした.
プリズムの偏角の問題は解きなれていないと,時間がかかりそうですね.
プリズムの問題は3つのことに着目して問題を解きましょう!




コメント