
一様で軽いばねのばね定数$k$は,ばねの長さ$l$に反比例するんだよね.
つまり,
$k\varpropto \dfrac{1}{l}$
いろんなところで使うからなんとなく覚えていたけど,なんで反比例するの?

ばね定数$k$が長さ$l$に反比例する理由ですか.
それでは,まずばね定数とは何か,というところから話しましょう.
フックの法則
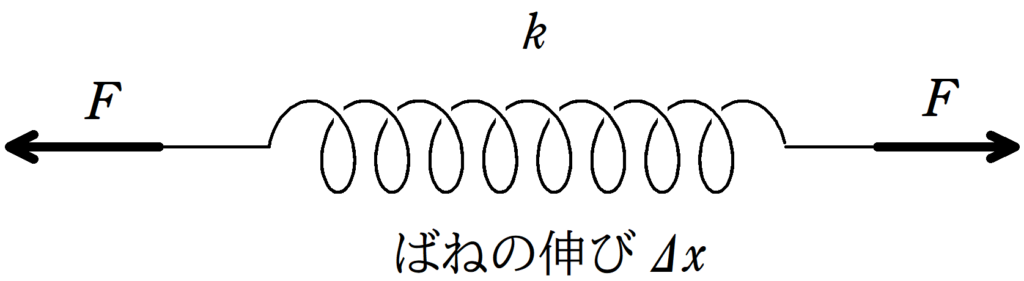

一様で軽いばねを考えましょう.
ばねに力$F$を両端に加えて,ばねをを伸ばします.
このとき,ばねを伸ばすのに必要な力はばねの伸び$\Delta x$に比例することが知られています.
つまり,ばねを伸ばせば伸ばすほど大きな力を加える必要があります.
もちろん,比例関係が成り立つ限界はありますが,ここでは,比例関係が成り立つ範囲で考えましょう.
比例定数を$k$とすると
$F=k\Delta x$
の関係が成り立ちます.
このときの$k$をばね定数と呼びます.

フックの法則だよね.
同じ$\Delta x$伸ばすのに必要な力が大きいとき,ばね定数は大きくなるから,硬いばねといえるね.
逆に,ばねを伸ばすのに必要な力が小さいときは,ばね定数が小さくなるので,やわらかいばねということだね.

はい.一応注意点としては,ばねに加える力は右側と左側それぞれ$F$の力を加えているのですが,$2F=k\Delta x$ではないということですね.
さて,次に2つのばねを直列に結んだときにはたらく力を考えてみましょう.
2つのばねにはたらく力(直列)


青いばねと赤いばねがあるね.
青いばねの左側には$f_{青左}$の力が,赤いばねの右側には$f_{赤右}$の力がかけらている.
さらに,ばねを伸ばすときにばねから手が受ける力が$f_{左}$と$f_{右}$だね.

はい.
そして,赤いばねが青いばねを引っ張る力が$f_{青右}$で,青いばねが赤いばねを引く力が$f_{赤左}$です.
それでは,作用反作用の関係にあるものはどれですか?

$f_{左}$と$f_{青左}$,$f_{青右}$と$f_{赤左}$,$f_{赤右}$と$f_{右}$だね.

その通りです.また,ばねの質量を無視しているので,運動していようと静止していようと,ばねにはたらく力の和は0になります.
$ma=F$
について,$m=0$のとき,
$F=0$
だからですね.

ということは,$f_{青左}$と$f_{青右}$の力の大きさは同じだし,$f_{赤左}$と$f_{赤右}$の力も大きさも同じなんだ!
結局
$f_{左}$,$f_{青左}$,$f_{青右}$,$f_{赤左}$,$f_{赤右}$,$f_{右}$
すべての力の大きさが同じなんだね!

そういうことです.だから,ばねを直列に接続した場合は,どのばねにも平等に同じ力がはたらくわけですね.
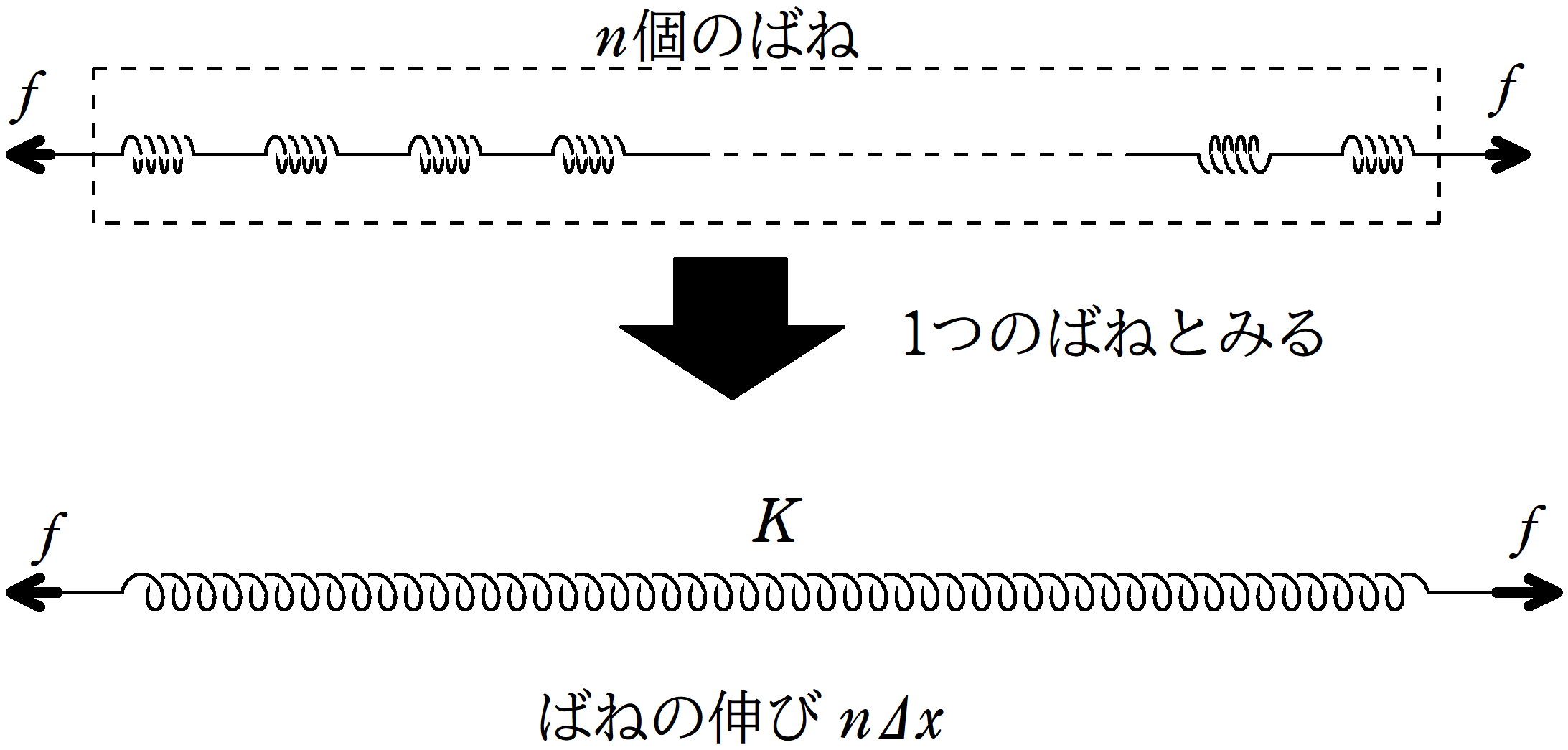
これを踏まえた上で,$n$個のばねをについて考えてみましょう.
$n$個のばねを直列に結ぶ
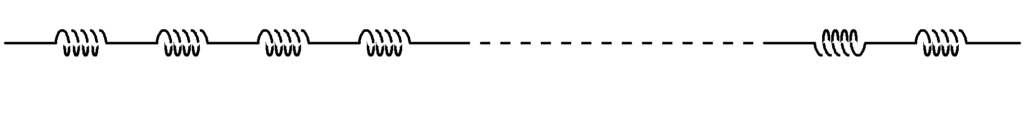

2つのばねのときと同じように考えることができるね.
力$f$を両端に加えると,すべてのばねに同じ力$f$がかかるんだ.


では,1つあたりのばね定数を$k$として,1つのばねの両端に力$f$を加えると,$\Delta x$伸びるとしましょう.
すると,$n$個のばね全体の伸びはいくらになるでしょう?

どのばねも力$f$で引っ張られていて,1つあたり$\Delta x$伸びるばねが$n$個あるんだから,全体のばねの伸びは$n\Delta x$だね.

はい.
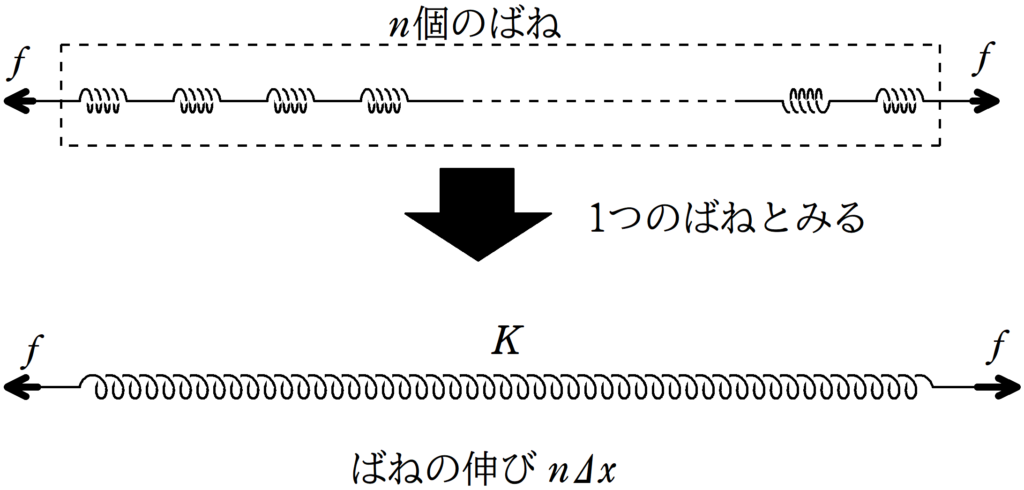
では,$n$個のばねを1つのばねとみてみましょう.
このばね定数を$K$とします.全体に加えている力が$f$でばねの伸びが$n\Delta x$なので,フックの法則より
$f=K\cdot n\Delta x$ $\dots (\ast)$
ですね.
そして,1つあたりのばねに着目してフックの法則を考えれば
$f=k\Delta x$ $\dots (2\ast)$
です.
$(\ast)$と$(2\ast)$から
$K=\dfrac{k}{n}$ $\dot (\clubsuit)$
となります.

$n$が長さに相当するんだね.$n=\alpha l$とすれば$(\clubsuit)$は
$K=\dfrac{k}{\alpha l}$
つまり,
$K\varpropto \dfrac{1}{l}$
になるね!

そういうことです.それでは,$K\varpropto \dfrac{1}{l}$を使った問題を解いてみましょう.
ばね定数$\varpropto \dfrac{1}{長さ}$ を利用した問題
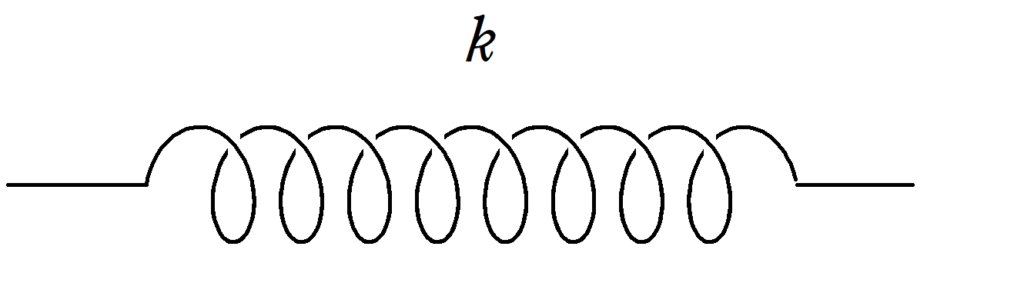
ばね定数$k$のばねを次のように分割したときのそれぞれのばね定数を求めよ.
(1) ばねを半分に分割する.
(2) ばねを左から$2:3$で分割する.
(3) ばねを左から$4:5$で分割する.
<解答> 分割したばねを左から$k_{L}$,$k_{R}$と名前を付けましょう.
(1) ばね定数は長さに反比例するので
$k_{L}:k=\dfrac{1}{\dfrac{1}{2}}:\dfrac{1}{1}=2:1$
したがって,
$k_{L}=2k$
$k_{R}$も同様に計算して,$k_{R}=2k$
(2) ばね定数は長さに反比例するので
$k_{L}:k=\dfrac{1}{\dfrac{2}{5}}:\dfrac{1}{1}=5:2$
したがって,
$k_{L}=\dfrac{5}{2}k$
同様に
$k_{R}:k=\dfrac{1}{\dfrac{3}{5}}:\dfrac{1}{1}=5:3$
したがって,
$k_{R}=\dfrac{5}{3}k$
(3) ばね定数は長さに反比例するので
$k_{L}:k=\dfrac{1}{\dfrac{4}{9}}:\dfrac{1}{1}=9:4$
したがって,
$k_{L}=\dfrac{9}{4}k$
同様に
$k_{R}:k=\dfrac{1}{\dfrac{5}{9}}:\dfrac{1}{1}=9:5$
したがって,
$k_{R}=\dfrac{9}{5}k$

ばね定数$\varpropto \dfrac{1}{長さ}$は覚えていれば使い方は難しくないね!
まとめ
- 一様で軽いばねはどの部分もはたらく力が同じである.
- そのため,力を加えるとばねが長ければ長いほど各部分が伸びる.
- ばね定数は単位長さ伸ばすのに必要な力であるから,ばねが長いほどその力は小さく済む.
- 以上のことをイメージして$k\varpropto \dfrac{1}{l}$を思い出す.


コメント
[…] […]
[…] […]
[…] […]
[…] […]
[…] [よくある質問]なぜばね定数は長さに反比例するのか? […]