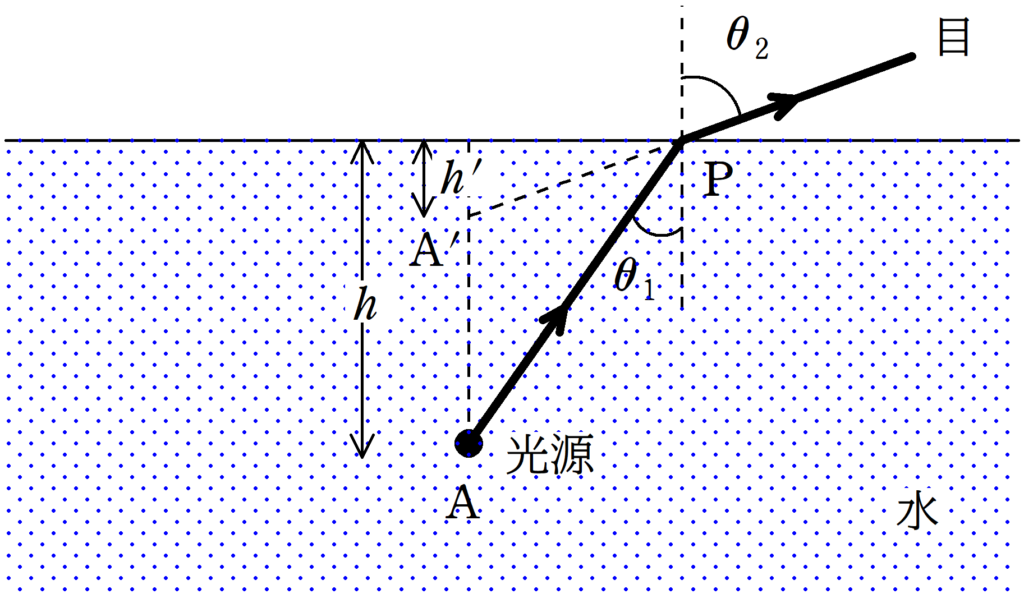
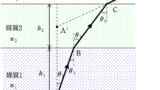
空気に対する相対屈折率$n$の水中の点Aに光源をおいた.点Aは深さ$h$の場所にある.図の太線は,光源から出た光が空気中にある目に届くまでの概略図である.
光源から出た光の入射角を$\theta_{1}$,屈折角を$\theta_{2}$とする.このとき,次の問いに答えよ.
(1) $n$,$\theta_{1}$,$\theta_{2}$の関係式をかけ.
(2) Aの真上付近の空気中からみると光源は$\rm A^{\prime}$にあるように見えた.$\rm A^{\prime}$の深さ$h^{\prime}$を$\theta_{1}$,$\theta_{2}$,$h$を用いて表せ.
(3) $\theta_{1}$,$\theta_{2}$が非常に小さいとき,次の近似式が成り立つ.
$\tan\theta_{1}\fallingdotseq \sin\theta_{1}\fallingdotseq \theta_{1}$
$\tan\theta_{2}\fallingdotseq \sin\theta_{2}\fallingdotseq \theta_{2}$
このとき,(2)の$h^{\prime}$を$n , h$を用いて表せ.
<解答>
(1)

屈折の法則を確認しましょう.
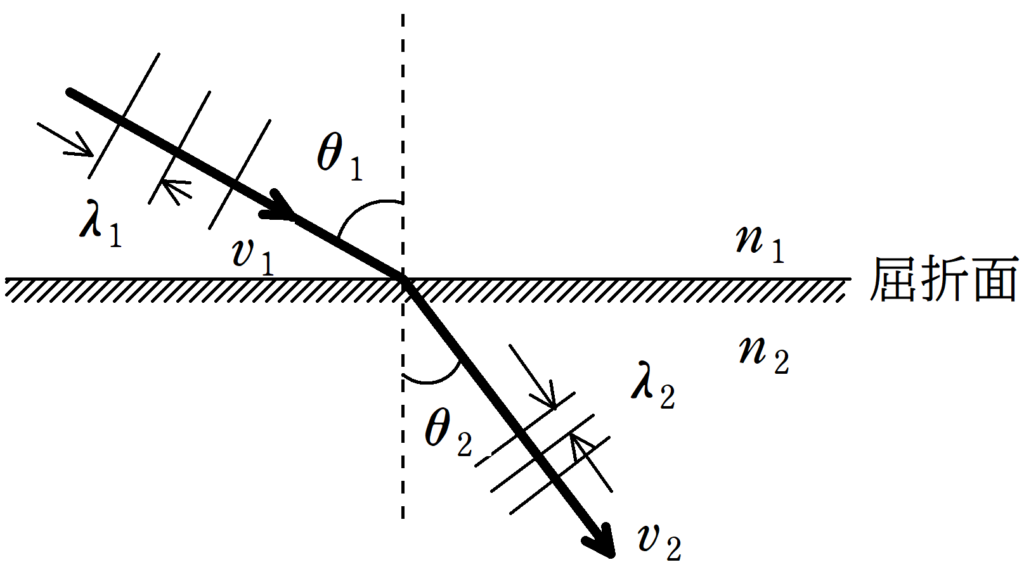
速さ$v_{1}$,波長$\lambda_{1}$の波が入射角$\theta_{1}$で屈折面に入射し,その後屈折角が$\theta_{2}$,速さ$v_{2}$,波長が$\lambda_{2}$となった.入射側の媒質の屈折率を$n_{1}$,屈折する側の媒質の屈折率を$n_{2}$とすると,次の関係が成り立つ.
$\dfrac{v_{1}}{v_{2}}=\dfrac{\sin\theta_{1}}{\sin\theta_{2}}$
また,屈折により,媒質の振動数$f$および周期$T$は変化しないことから,次のことが成り立つ.
$\dfrac{v_{1}}{v_{2}}=\dfrac{\cancel{f}\lambda_{1}}{\cancel{f}\lambda_{2}}=\dfrac{\lambda_{1}}{\lambda_{2}}$
一方,屈折率との関係は次のようになる.
$n_{1}\sin\theta_{1}=n_{2}\sin\theta_{2}$
$n_{1}v_{1}=n_{2}v_{2}$
$n_{1}\lambda_{1}=n_{2}\lambda_{2}$
最後に,$n_{12}=\dfrac{n_{2}}{n_{1}}$を屈折率$n_{1}$の媒質に対する屈折率$n_{2}$の媒質の相対屈折率という.

「空気に対する相対屈折率$n$」というのは,空気の屈折率を$1$としたときに水中の屈折率が$n$と考えればよいです.
したがって,屈折の法則より,次の関係式が成り立ちます.
★ 屈折の法則
$n\sin\theta_{1}=1\cdot \sin\theta_{2}$(答)
(2)

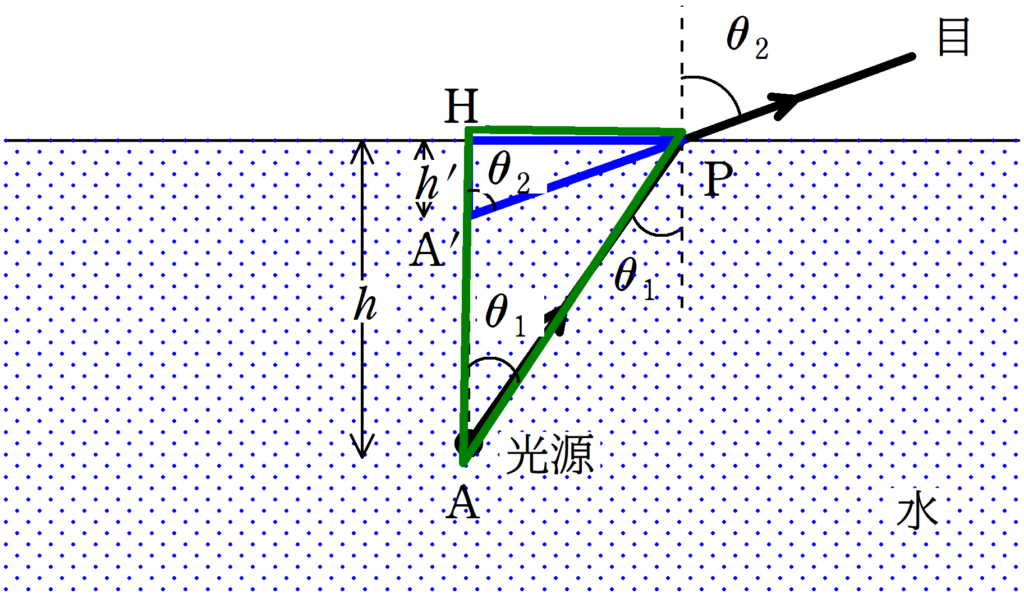
直線$\rm AA^{\prime}$と水面との境界線との交点をHとします.
みかけの深さの問題ではよくあるのですが,下図のHPを共通な辺にもつ三角形$\rm AHP$と三角形$\rm A^{\prime}HP$を考えます.
この2つの三角形それぞれについて,$\rm HP$の長さを表すと
${\rm HP}=h\tan\theta_{1}=h^{\prime}\tan\theta_{2}$
となり,
$h^{\prime}=\dfrac{\tan\theta_{1}}{\tan\theta_{2}}h$(答)
を得ます.
(3)

最後は,問題文で与えられている近似と(1)の結果を使いましょう.
$\tan\theta_{1}\fallingdotseq \sin\theta_{1}$および,$\tan\theta_{2}\fallingdotseq \sin\theta_{2}$と,(1)の$\dfrac{\sin\theta_{1}}{\sin\theta_{2}}=\dfrac{1}{n}$を用いて
$\eqalign{h^{\prime}&=\dfrac{\tan\theta_{1}}{\tan\theta_{2}}h\\&\fallingdotseq \dfrac{\sin\theta_{1}}{\sin\theta_{2}}h\\&=\dfrac{h}{n}}$

ということで,答えは,$h^{\prime}=\dfrac{h}{n}$(答)となります.$n>1$のとき,少し浅いところに浮き上がって見えるんだね.

次回の内容はこちらです.



コメント
[…] […]