
$^{2}_{1}{\rm H}+^{2}_{1}{\rm H}\to ^{1}_{1}{\rm p}+^{3}_{1}{\rm H}$
$^{2}_{1}{\rm H}$の結合エネルギーが$A$,$^{3}_{1}{\rm H}$の結合エネルギーが$B$のとき,この核反応で生じるエネルギーは$A,B$を用いてどのように表されると思いますか?

左辺のエネルギーが$2A$,右辺のエネルギーが$B$だから,$2A-B$が核反応で生じるエネルギーなんじゃない?

残念ですが,正しい答えは,$B-2A$です.

え?,だって左辺のエネルギーが$100$でそこからエネルギーが発生して右辺のエネルギーが$60$になったとしたら,発生したエネルギーは$100-60=40$,つまり,左辺のエネルギーから右辺のエネルギーを引けばいいんじゃないの??

実は「結合エネルギー」はその原子核のもっているエネルギーを表しているわけではなく,原子核をばらばらにするのに必要なエネルギーなんです.
結合エネルギーとは,原子核を陽子や中性子に分裂させるために必要なエネルギー

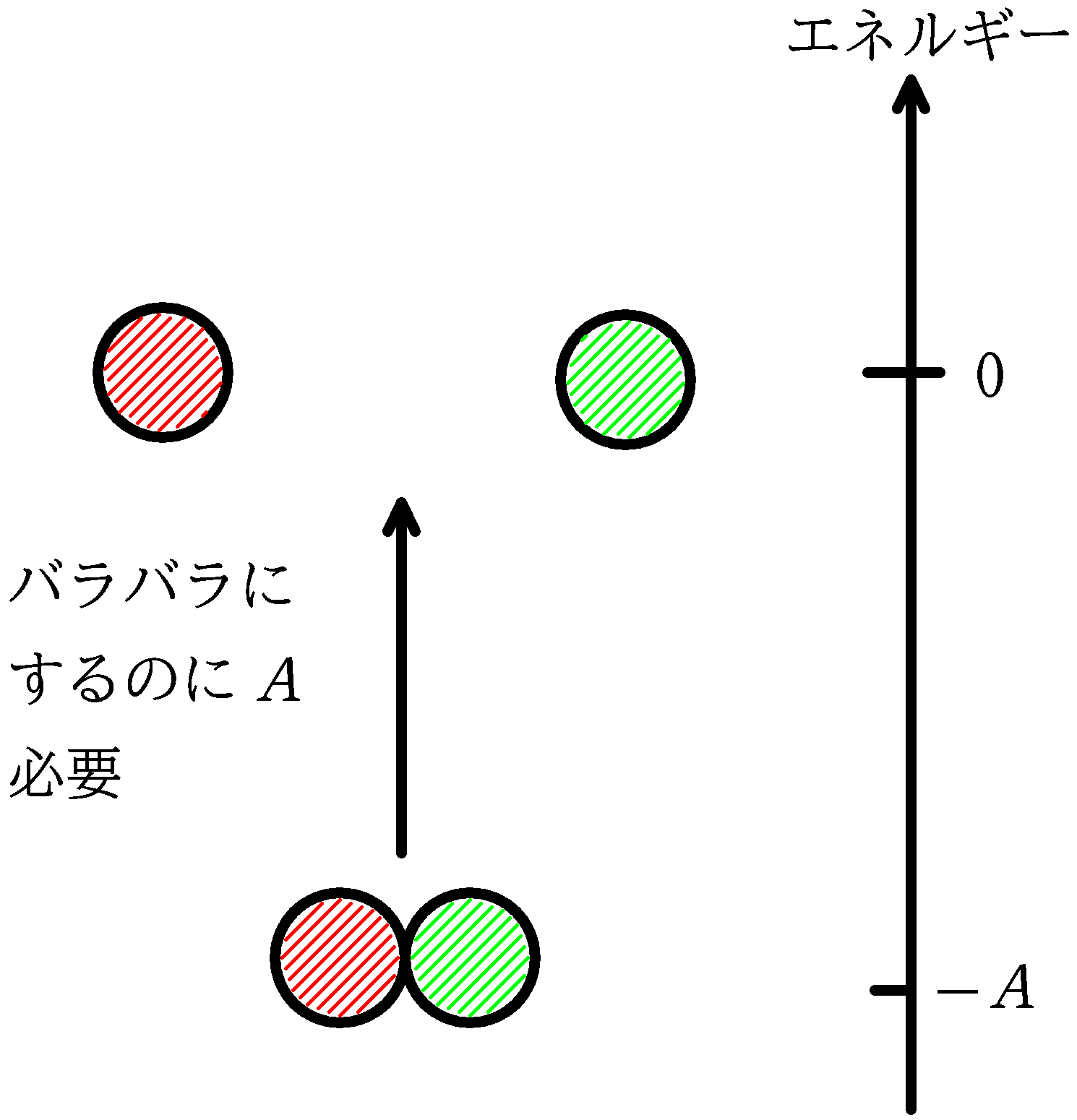
原子核をバラバラにするのにエネルギーが必要だろうから,バラバラの状態は原子核のようにまとまっている状態よりエネルギーが高い状態なんだね.そして,他の原子核と比較するにはエネルギーの基準が必要になってくるね.

バラバラの状態はそれぞれの原子核が達する最高のエネルギーというところで同じなので,バラバラの状態をエネルギーの基準とするとよいでしょう.
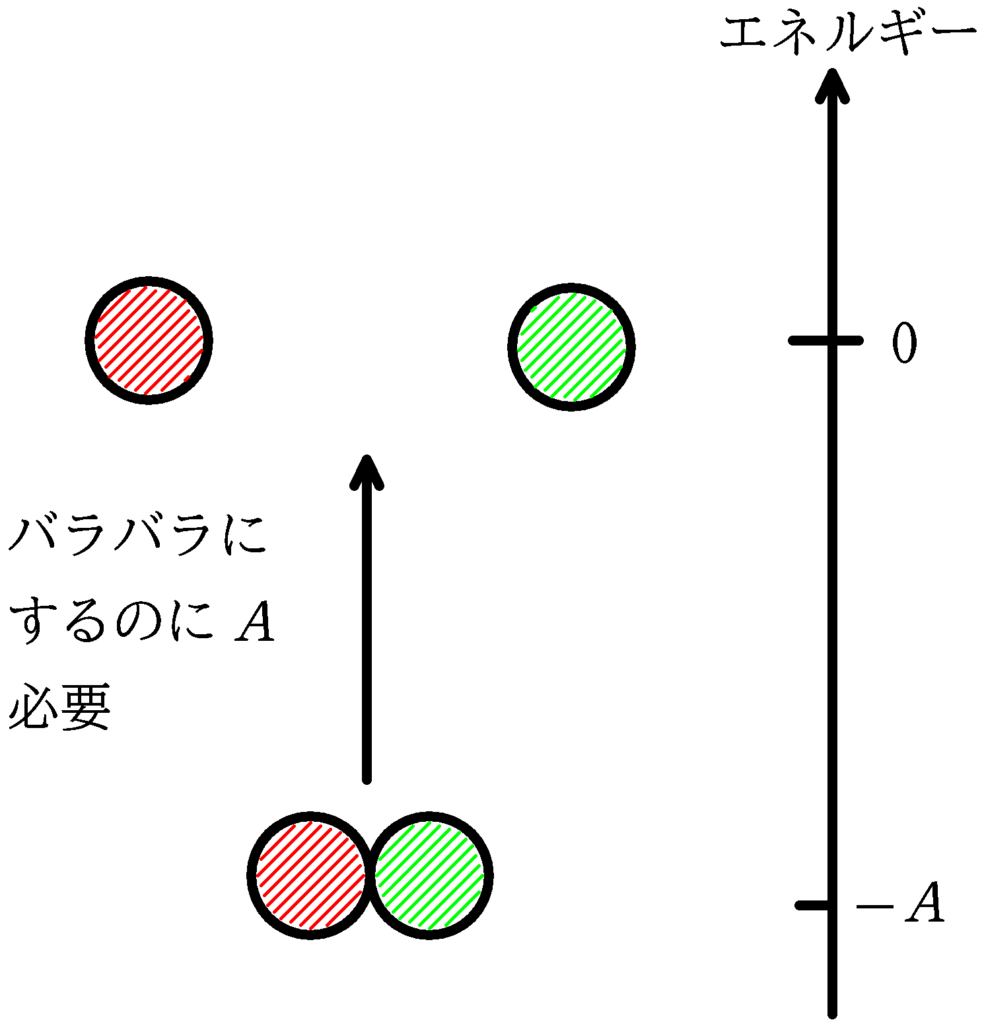

結合エネルギーが与えられたときの核反応によって生じるエネルギーの計算の場合は結合エネルギーを$A$とすると,エネルギーを$-A$として計算するんだね.
さっきの問題であったら,こうやっておけばいいんだね.
$^{2}_{1}{\rm H}+^{2}_{1}{\rm H}\to ^{1}_{1}{\rm p}+^{3}_{1}{\rm H}$
$^{2}_{1}{\rm H}$の結合エネルギーが$A$,$^{3}_{1}{\rm H}$の結合エネルギーが$B$のとき,この核反応で生じるエネルギーは$A,B$を用いてどのように表されると思いますか?
<解答> 発生するエネルギーを$E$とすると
$-A=-B+E$ $\therefore\,\, E=B-A$ (答)
結合エネルギーが$A$のとき,原子核のエネルギーを$-A$として計算するとよい.

最後に演習問題で確認しましょう.
問題で与えているのが「核子1個あたり」の結合エネルギーであることに注意してください.
$^{2}_{1}{\rm H},^{3}_{1}{\rm H},^{3}_{2}{\rm He},^{4}_{2}{\rm He}$それぞれの核子1個当たりの結合エネルギーがそれぞれ$1.11\,\rm MeV,2.83\,MeV,2.57\,MeV,7.07\,MeV$であるとき,次の核反応で発生するエネルギーを求めよ.
(1) $^{2}_{1}{\rm H}+^{2}_{1}{\rm H}\to ^{1}_{1}{\rm p}+^{3}_{1}{\rm H}$
(2) $^{2}_{1}{\rm H}+^{2}_{1}{\rm H}\to ^{1}_{0}{\rm n}+^{3}_{2}{\rm He}$
(3) $^{2}_{1}{\rm H}+^{3}_{1}{\rm H}\to ^{1}_{0}{\rm n} +^{4}_{2}{\rm He}$
(4) $^{2}_{1}{\rm H}+^{3}_{2}{\rm He}\to ^{1}_{1}{\rm p}+^{4}_{2}{\rm He}$
<解答>
(1) $^{2}_{1}{\rm H}$の核子は2個なので,結合エネルギーは$1.11\times 2=2.22\,{\rm MeV}$.左辺はこれが2つある.また,$^{3}_{1}{\rm H}$の核子が3個なので,結合エネルギーは$2.83\times 3=8.49\,\rm MeV$.発生するエネルギーを$E_{1}\,[\rm MeV]$として
$-2.22+(-2.22)=-8.49+E_{1}$ $\therefore\,\, E_{1}=4.05\,\rm MeV$ (答)
(2) $^{2}_{1}{\rm H}$の核子は2個なので,結合エネルギーは$1.11\times 2=2.22\,{\rm MeV}$.左辺はこれが2つある.また,$^{3}_{2}{\rm He}$の核子は3個なので,$2.57\times 3=7.71\,\rm MeV$.発生するエネルギーを$E_{2}\,[\rm MeV]$として
$-2.22+(-2.22)=-7.71+E_{2}$ $\therefore\,\, E_{2}=3.27\,\rm MeV$ (答)
(3) $^{2}_{1}{\rm H}$の核子は2個なので,結合エネルギーは$1.11\times 2=2.22\,{\rm MeV}$.$^{3}_{1}{\rm H}$の核子は3個であるから,結合エネルギーは$2.83\times 3=8.49\,\rm MeV$.また,$^{4}_{2}{\rm He}$の核子は4個なので,結合エネルギーは$7.07\times 4=28.28\,\rm MeV$.発生するエネルギーを$E_{3}\,[\rm MeV]$として
$-2.22+(-8.49)=-28.28+E_{3}$ $E_{3}=17.57\fallingdotseq 17.6\,\rm MeV$ (答)
(4) $^{2}_{1}{\rm H}$の核子は2個なので,結合エネルギーは$1.11\times 2=2.22\,{\rm MeV}$.$^{3}_{2}{\rm He}$の核子は3個なので,$2.57\times 3=7.71\,\rm MeV$.また,$^{4}_{2}{\rm He}$の核子は4個なので,結合エネルギーは$7.07\times 4=28.28\,\rm MeV$.発生するエネルギーを$E_{4}\,[\rm MeV]$として
$-2.22+(-7.71)=-28.28+E_{4}$ $E_{4}=18.35\fallingdotseq 18.4\,\rm MeV$ (答)


コメント