
今回は,発展問題でもよくでてくる重心の話をしていきます.
重心とは何か?
重心速度とは?
重心加速度とは?
そもそもなぜ重心を考えるのか?
を説明します.
重心の定義

重心$x_{\rm G}$は次のように定義しています.
座標$x_{1}$,$x_{2}$にそれぞれ質量$m_{1}$,$m_{2}$の物体がある.
このときの重心の位置$x_{\rm G}$は
$x_{\rm G}=\dfrac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}$

この式は,次のように理解してください.
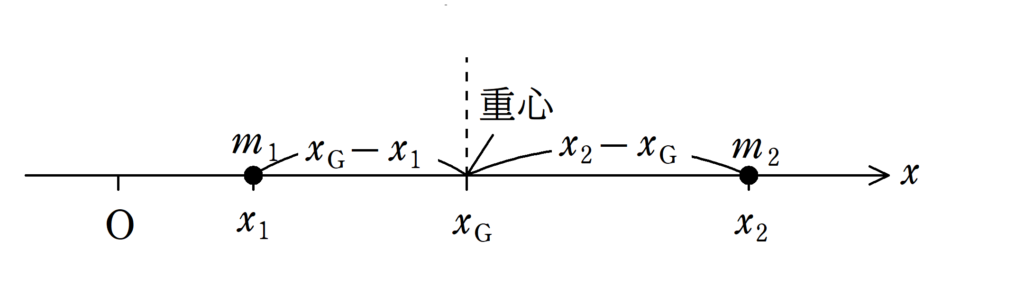
質量$m_1$の物体が座標$x_1$の位置にあり,質量$m_2$の物体が座標$x_2$にあるとき,重心は力のモーメントがつり合う場所と考えます.
すなわち,上図において,重心を中心としたとき,$m_1$,$m_2$の物体の重心からの距離はそれぞれ,$x_{\rm G}-x_1$ , $x_{2}-x_G$であるから,モーメントのつり合いは
$\eqalign{m_{1}(x_{\rm G}-x_1)&=m_{2}(x_{2}-x_G)\cr (m_{1}+m_{2})x_{\rm G}&=m_{1}x_{1}+m_{2}x_{2}\cr x_{\rm G}&=\dfrac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}}$
重心速度

それぞれの物体が動くと,それにともない重心も動きます.
重心の速度を重心速度といいます.
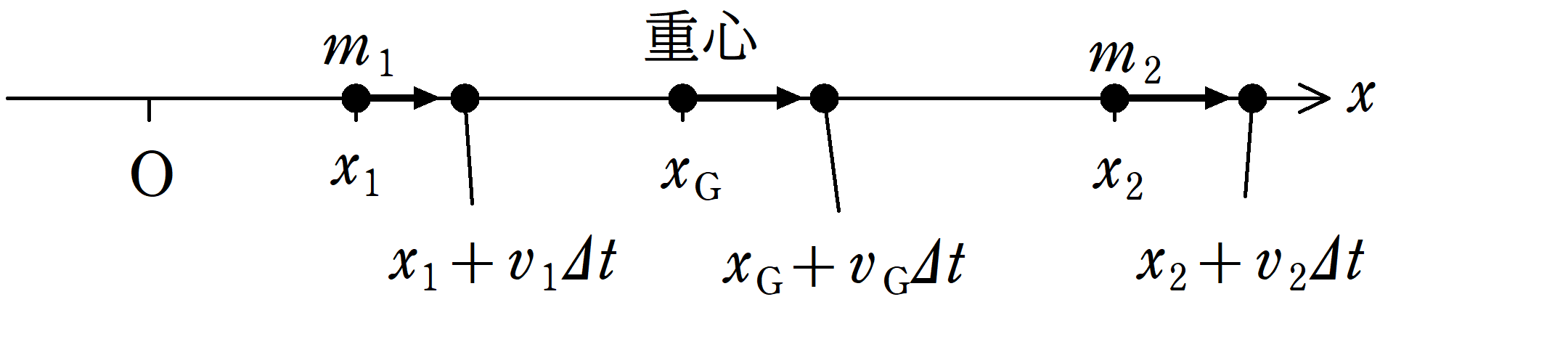
質量$m_1$,$m_2$の物体の速度をそれぞれ$v_1$,$v_2$とし,さらに,重心速度を$v_G$とします.
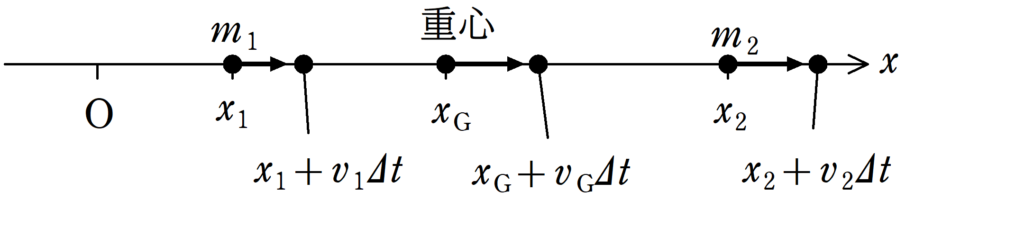
すると,$\Delta t$の間に次のようにそれぞれ位置が変化します.

速度の定義
$v=\dfrac{\Delta x}{\Delta t}$
を変形して
$\Delta x=v\Delta t$
が位置の変化分だね.,
時間$\Delta t$後の重心の位置は,重心の定義式より
$\eqalign {x_{\rm G}+v_{\rm G} \Delta t &=\dfrac{m_{1}(x_{1}+v_{1} \Delta t )+m_2(x_{2}+v_{2} \Delta t)}{m_1+m_2} \\ &= \dfrac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2} }+\dfrac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}\Delta t }$
$x_{\rm G}=\dfrac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}$より,
$v_{\rm G} \Delta t=\dfrac{m_{1}v_{1}+m_{2}v_{2}}{m_1+m_2}\Delta t$
両辺$\Delta t$で割れば
$v_{\rm G}=\dfrac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}$
を得ます.これが重心速度の式です.
速度$v_{1}$,$v_{2}$をもつ質量$m_{1}$,$m_{2}$の物体がある.
このときの重心速度$v_{\rm G}$は
$v_{\rm G}=\dfrac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}$
重心加速度

同様にして,重心加速度も定義します.
つまり,物体がそれぞれ加速度運動すれば,重心も加速度運動します.
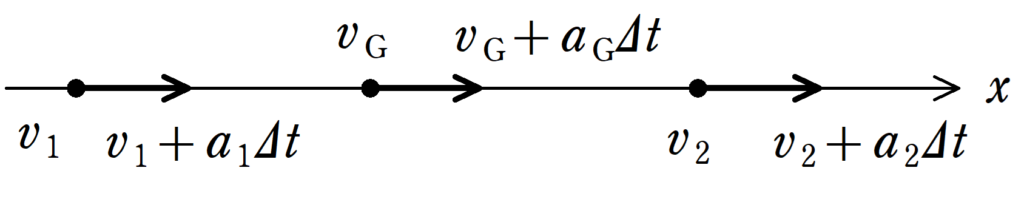

これも,加速度の定義
$a=\dfrac{\Delta v}{\Delta t}$
を変形して
$\Delta v=a\Delta t$
が速度の変化分だね.
時間$\Delta t$後の重心速度の式は
$\eqalign{v_{\rm G}+a_{\rm G}\Delta t&=\dfrac{m_{1}(v_{1}+a_{1}\Delta t)+m_{2}(v_{2}+a_{2}\Delta t)}{m_{1}+m_{2}}\\&=\dfrac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}+\dfrac{m_{1}a_{1}+m_{2}a_{2}}{m_{1}+m_{2}}\Delta t}$
$v_{\rm G}=\dfrac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}$より
$a_{\rm G}\Delta t =\dfrac{m_{1}a_{1}+m_{2}a_{2}}{m_{1}+m_{2}}\Delta t$
したがって
$a_{\rm G}=\dfrac{m_{1}a_{1}+m_{2}a_{2}}{m_{1}+m_{2}}$

重心も,重心速度も,重心加速度も同じような形をしていて覚えやすいね.
加速度$a_{1}$,$a_{2}$をもつ質量$m_{1}$,$m_{2}$の物体がある.
このときの重心加速度$a_{\rm G}$は
$a_{\rm G}=\dfrac{m_{1}a_{1}+m_{2}a_{2}}{m_{1}+m_{2}}$
重心の運動方程式

重心加速度は上の定義式を使って求めてもよいですが,次の重心の運動方程式を用いてもよいです.
質量$m_{1}$,$m_{2}$の物体の重心の加速度を$a_{\rm G}$とする.2つの物体にはたらいている力をそれぞれ$F_{1}$,$F_{2}$とすると,次の式が成り立つ.
$(m_{1}+m_{2})a_{\rm G}=F_{1}+F_{2}$

この式は,それぞれの物体の運動方程式を重心加速度の式に代入して整理したものとなっています.
★ 運動方程式
$m_{1}a_{1}=F_{1}$,$m_{2}a_{2}=F_{2}$
これらを,$a_{\rm G}=\dfrac{m_{1}a_{1}+m_{2}a_{2}}{m_{1}+m_{2}}$に代入して
$a_{\rm G}=\dfrac{F_{1}+F_{2}}{m_{1}+m_{2}}$
$\therefore (m_{1}+m_{2})a_{\rm G}=F_{1}+F_{2}$

質量の和×重心加速度=力の和
の形になっているんだね.
重心からみた運動量の和は0

さて,なぜこのような実体のない重心の運動なんてもを考えるのでしょうか?
実は,次のことから成り立つからなのです.
質量$m_{1}$,$m_{2}$の物体がある.
重心からみたそれぞれの速度を$v_{\rm G1}$,$v_{\rm G2}$とすると,次の式が成り立つ.
$m_{1}v_{\rm G1}+m_{2}v_{\rm G2}=0$
すなわち,重心からみた物体の運動量の和は0となる.

なぜ,このようなことが成り立つのかを説明しましょう.
いま,下図のように,緑くんと青くんが$x$軸上を運動しています.
その速度はそれぞれ$v_1$,$v_2$です.
また,緑くんと青くんの重心速度を$v_{\rm G}$とすると,$v_{\rm G}$は次のようになります.
$v_{\rm G}=\dfrac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}$
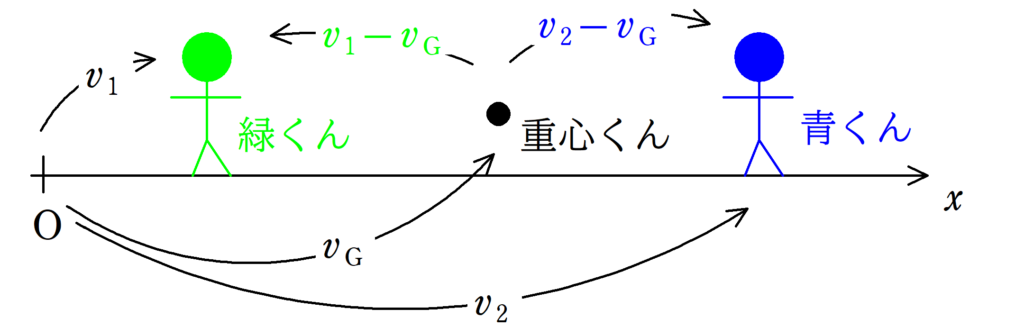

重心くんからみた緑くん,青くんの速度はそれぞれ,$v_{1}-v_{\rm G}$,$v_{2}-v_{\rm G}$なので,重心くんからみた緑くんと青くんの運動量の和は
$\eqalign{ m_{1}(v_{1}-v_{\rm G})+m_{2}(v_{2}-v_{\rm G}) &= m_{1}v_{1}-m_{1}v_{\rm G}-m_{2}v_{2}-m_{2}v_{\rm G} \\ &= (m_{1}v_{1}+m_{2}v_{2})-(m_{1}+m_{2})v_{\rm G} \\ &= (m_{1}v_{1}+m_{2}v_{2})- (m_{1}+m_{2}) \dfrac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}\\ &=(m_{1}v_{1}+m_{2}v_{2})-(m_{1}v_{1}+m_{2}v_{2}) \\&=0 }$
このようにして,重心からみた運動量の和が0になることが確認できます.
なぜ重心からみるのか?

“重心からみた運動量の和が0″であることを導いたときに,特別な条件は入れていません.
つまり,これはいつだって成り立つのです.
たとえば,質量が同じ物体について考えてみましょう.
このとき,重心からみた速度をそれぞれ$v_{\rm G1}$,$v_{\rm G2}$とすると
$mv_{\rm G1}+mv_{\rm G2}=0$
$\therefore$ $v_{\rm G1}=-v_{\rm G2}$

すなわち,重心から速度の大きさが同じで常に反対方向に速度をもつのです.
たとえ,2つの物体が複雑にバラバラに動いても,重心からみたら対称的に運動してくれます.

これが重心から物体の運動をみる理由の1つです.
「なんで実体のない重心の運動なんて考える必要があったんだろう?」と思っていた理由の答えは「重心からみると簡単な運動にみえる」からです.
難関大の入試では重心からみた運動を考えることも少なくありません.
演習を通して解き方を確認しておくとよいでしょう.


コメント
[…] […]
[…] […]
[…] 発展問題を解く際に必要な重心の知識 […]
[…] […]
[…] […]