レンズの演習問題⑨ 虚光源のレンズの式 | Physicmath（フィジクマス）

NEKO

レンズの式は，次のようになるんだったね．

レンズの式の統一

レンズと光源との距離を$|a|$，焦点距離を$|f|$，レンズと像との距離を$|b|$とする．

このとき，次の式が成り立つ．

$\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{f}$

ただし，次の規則で$b$と$f$の正負を決める．

$b>0　\dots$　実像，　$b<0　\dots$　虚像

$f>0　\dots$　，　凸レンズ　$f<0　\dots$　凹レンズ

NEKO

このとき，$a$が負の場合についても書いてあったんだけど，どういう意味なんだろう？？

PHYさん

それでは，$a$が負になる場合についての問題を扱っていきましょう．

問題の後に解説，最後にレンズの式のまとめもします．

前回の内容はこちら

問題　虚光源のレンズの式

次の(1)，(2)，(3)の図において$\rm F，F^{\prime}$は各レンズの焦点である．

レンズがないと仮定した場合に出来上がる像を虚物体または虚光源という．

虚物体とレンズの距離を$a$，焦点距離を$f$，レンズの屈折によって，実際にできる像とレンズの距離を$b$としたとき，$a,b,f$の関係式を(1),(2),(3)について，それぞれ求めよ．

(1)

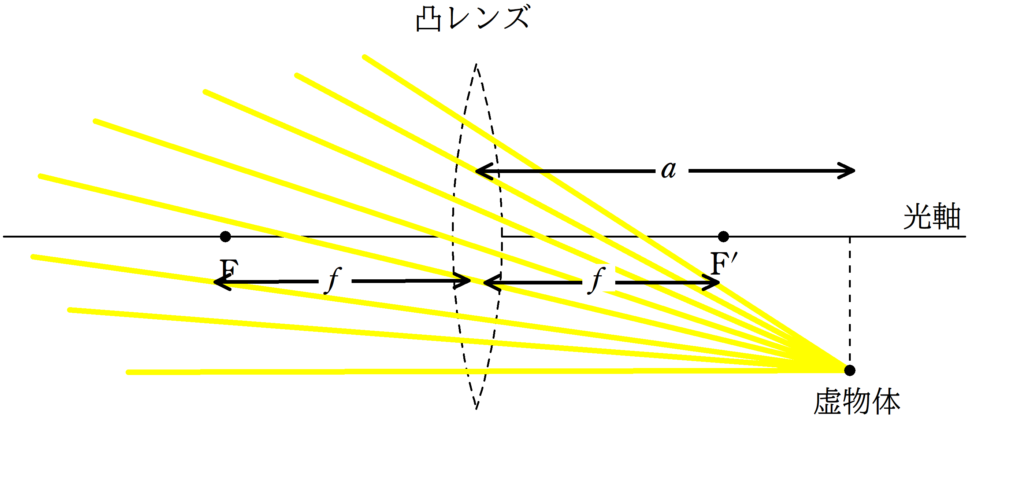
(2)

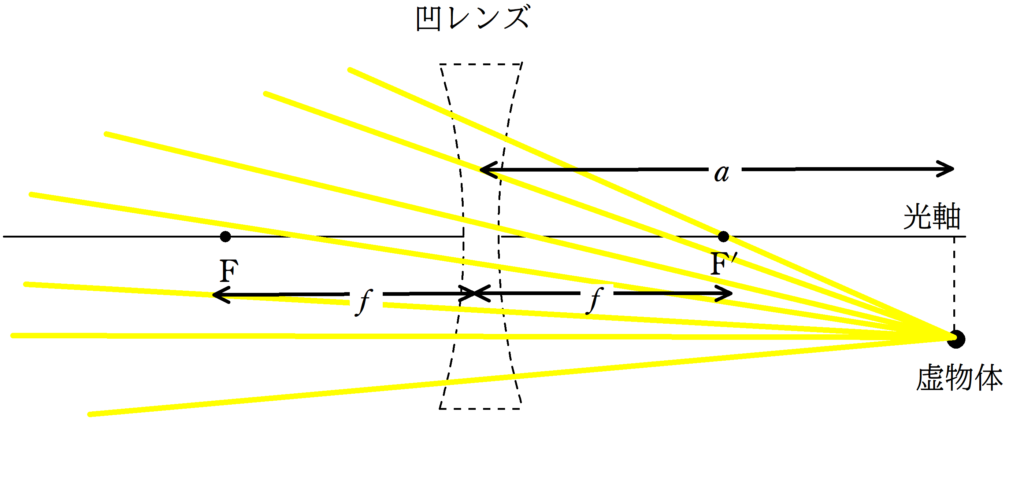
(3)

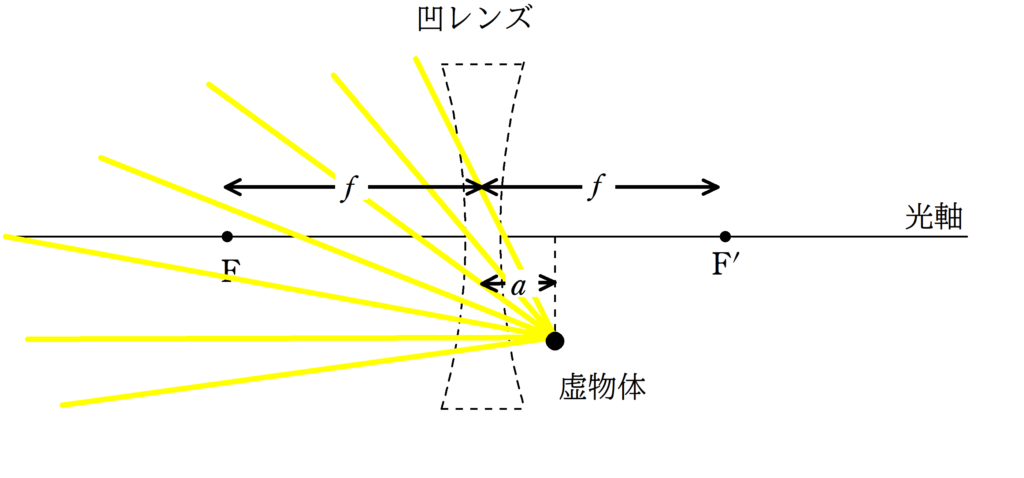
<解答>

NEKO

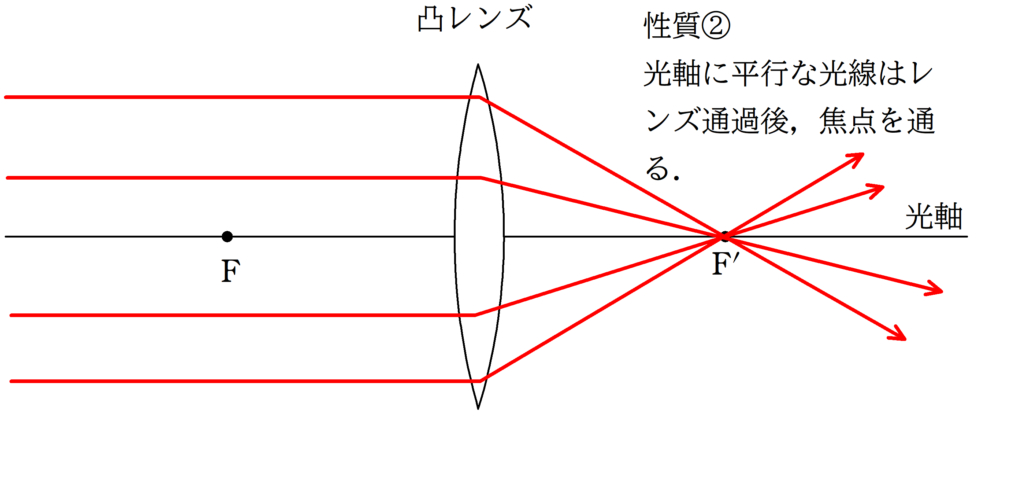
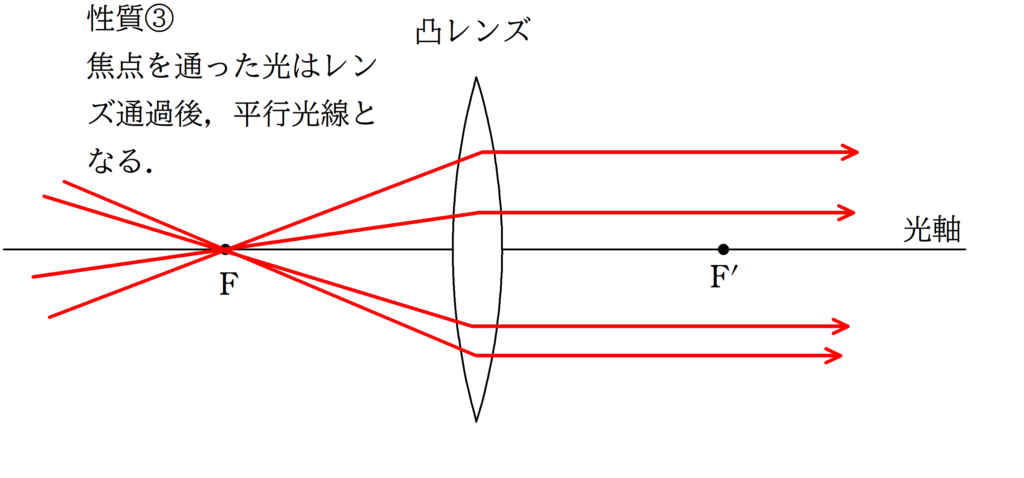
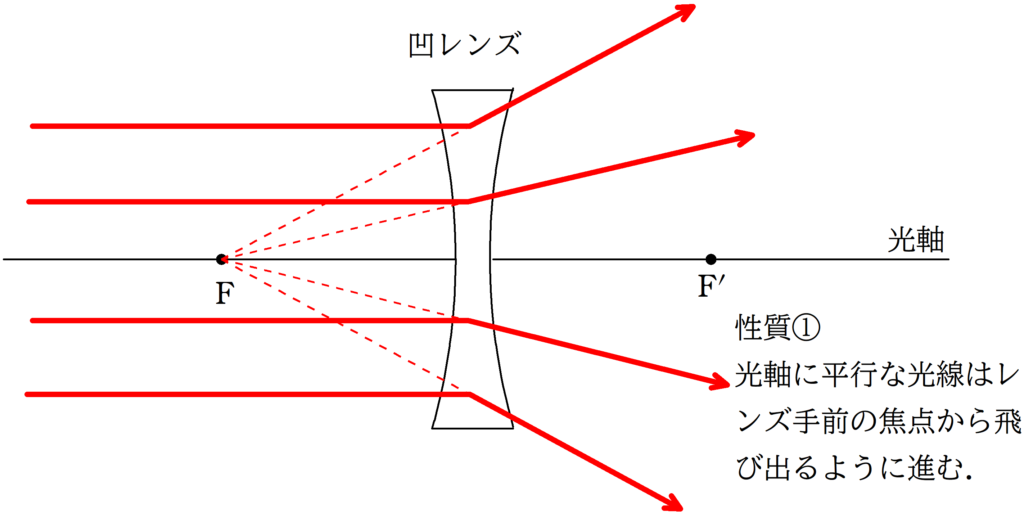
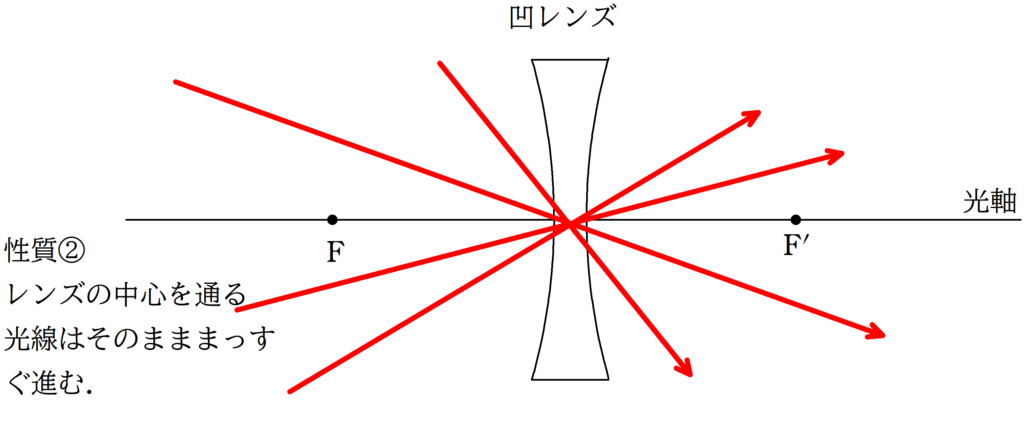
まずは，凸レンズと凹レンズの代表光線の復習をしておきましょう．

凸レンズの代表光線

凹レンズの3つの代表光線

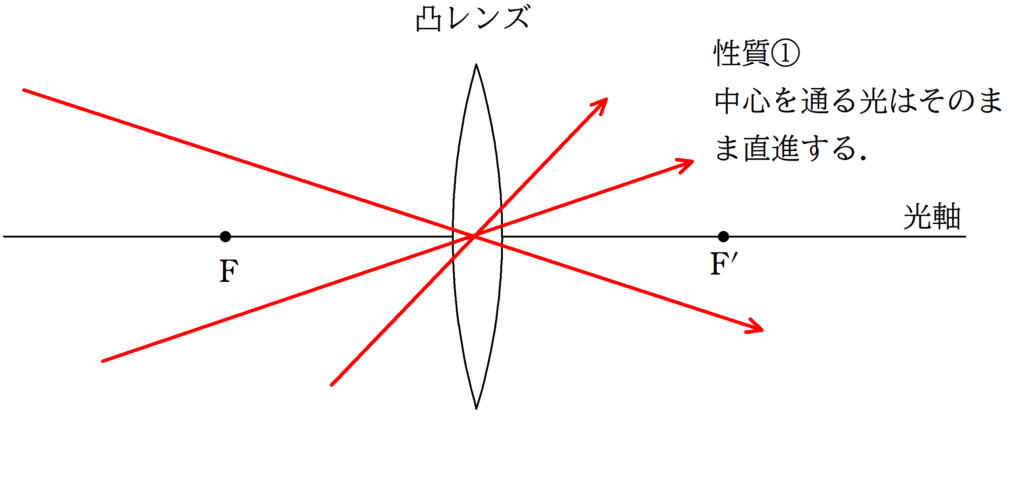
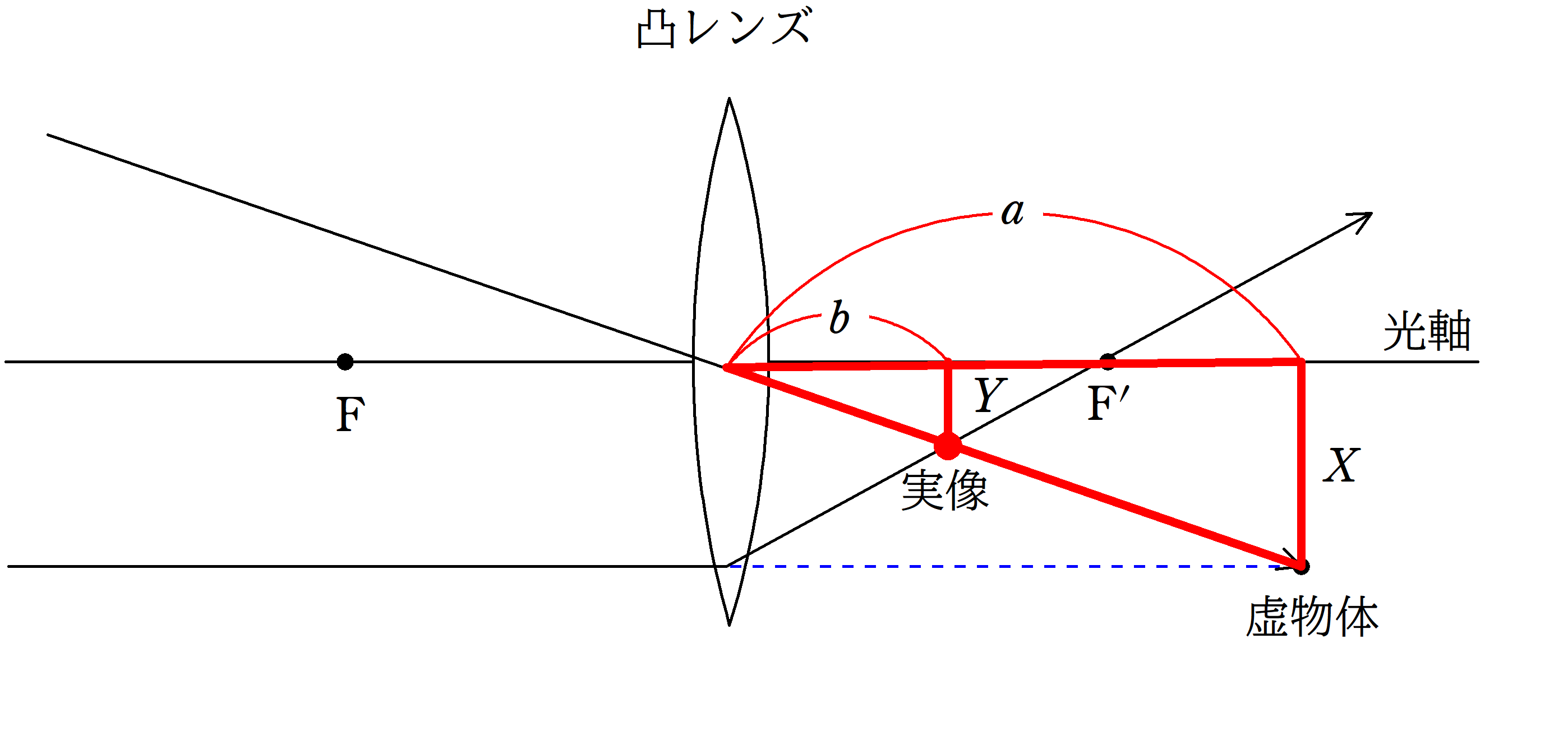
(1)

NEKO

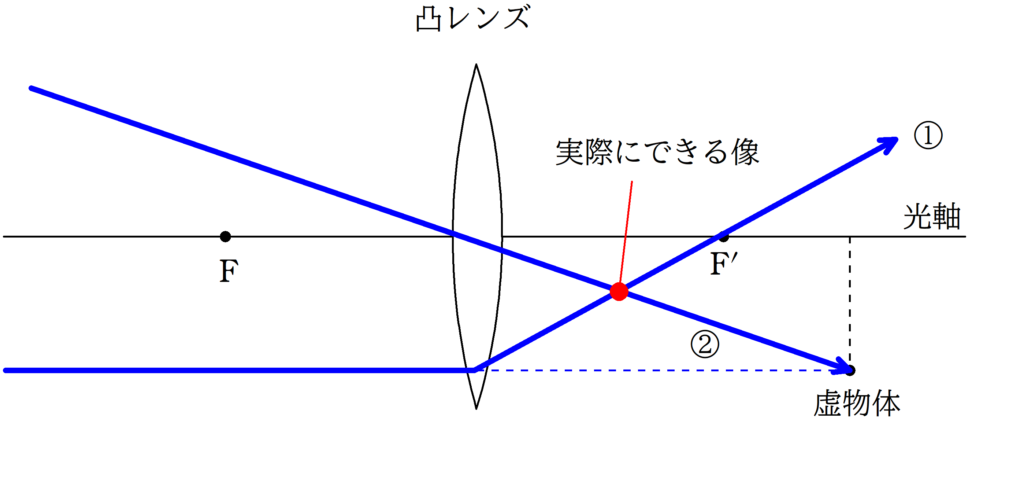
虚物体に向かう光線のうち

①：平行光線

②：中心を通る光線

をかくと，上図の赤い点で交点をもちます．

すると，すべての光線はこの赤い点に集まり，この場所に実像ができます．

NEKO

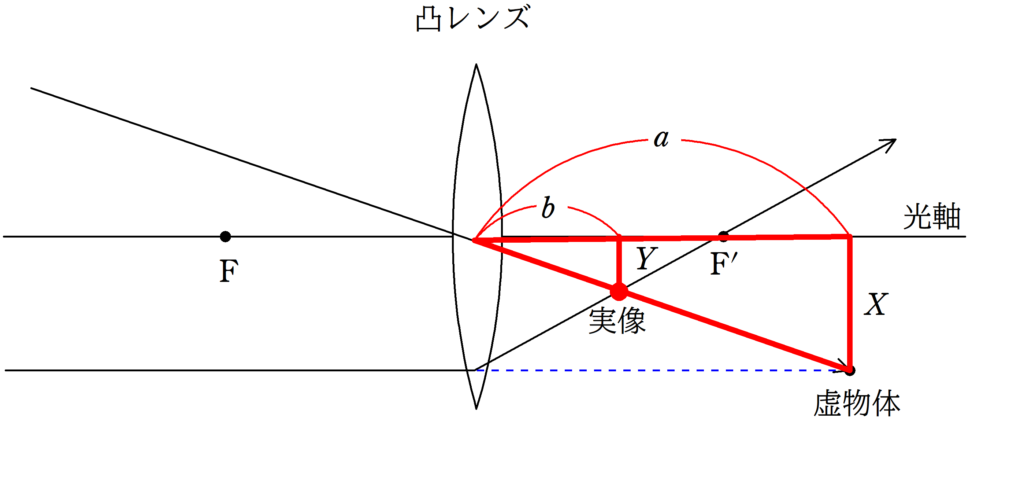
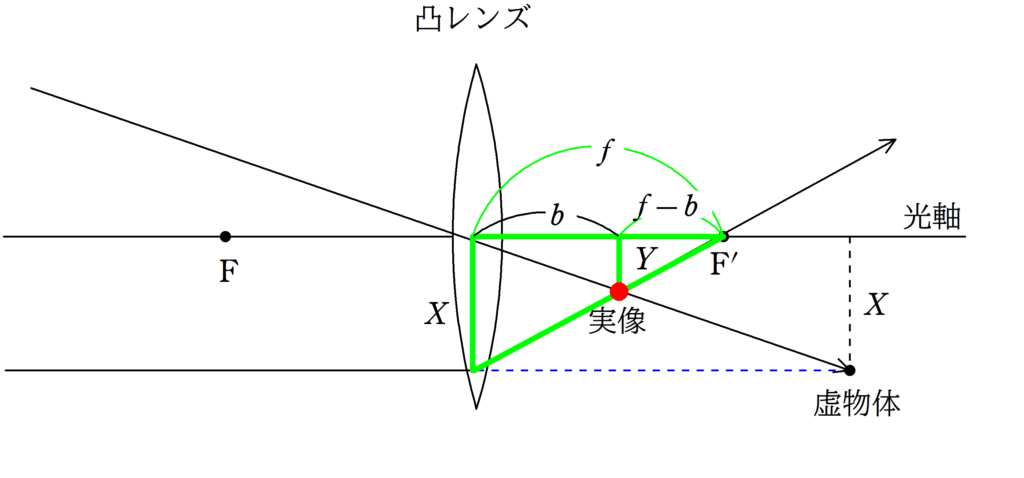
虚物体の高さを$X$，実像の高さを$Y$として，2組の相似な図形を見つけましょう．

上図のように，赤い方の相似な図形と緑の方の相似な図形の相似比を考えます．

★　赤の方の相似比

$\dfrac{Y}{X}=\dfrac{b}{a}$　$\cdots　(\ast)$

★　緑の方の相似比

$\dfrac{Y}{X}=\dfrac{f-b}{f}$　$\cdots　(2\ast)$

$(\ast)$と$(2\ast)$より

$\eqalign{\dfrac{b}{a}&=\dfrac{f-b}{f}\cr bf&=a(f-b) \cr bf&=af-ab}$

両辺$abf$で割って

$\dfrac{1}{a}=\dfrac{1}{b}-\dfrac{1}{f}$

NEKO

じゃあ，

$\dfrac{1}{a}-\dfrac{1}{b}=-\dfrac{1}{f}$

かな？？

PHYさん

もちろん，それも答えとして正しいです．

しかし，実像の場合は$b>0$，凸レンズは$f>0$としてきたので，今までに決めたルールとつじつまが合うように直してみると，次のようになります．

$\dfrac{1}{a}-\dfrac{1}{b}=-\dfrac{1}{f}$の両辺に$(-1)$をかけて

$-\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{f}$　(答)

NEKO

なるほど，このようにすれば，つじつまが合うのか．

ってことは，虚光源の場合は$a<0$とすればいいみたいだね．

PHYさん

はい．

それでは，他の場合もつじつまが合うのか調べてみましょう．

(2)

NEKO

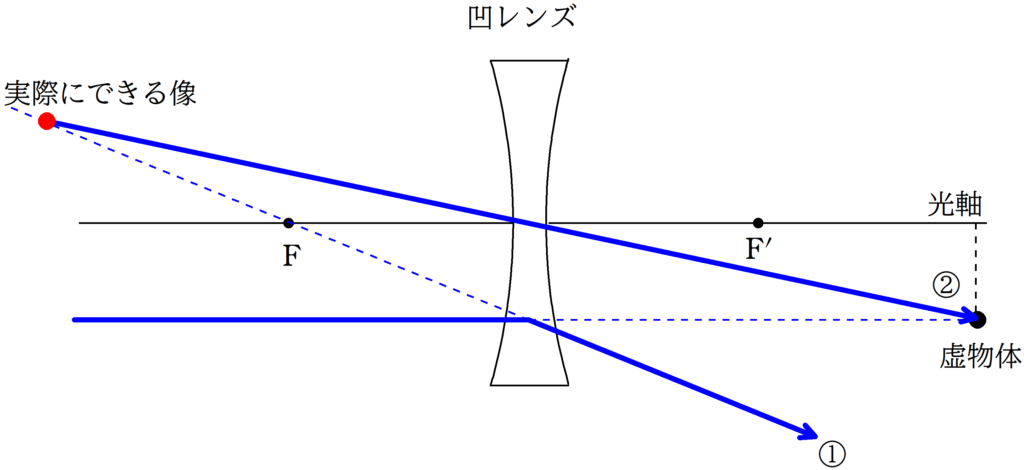
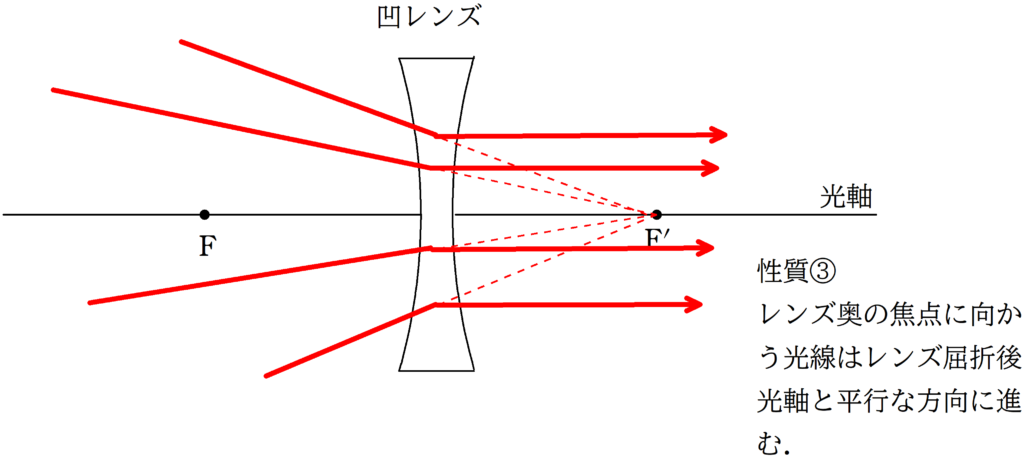
次に凹レンズです．

虚物体に向かう光線のうち，

①：平行光線

②：中心を通る光線

をかくと，上図のようになります．

これらの光線はレンズの右側で交わらないので，反対側に延長して，交点を求めます．

赤い点が虚像となり，すべての光は凹レンズ屈折後，赤い点から飛び出したように屈折していきます．

NEKO

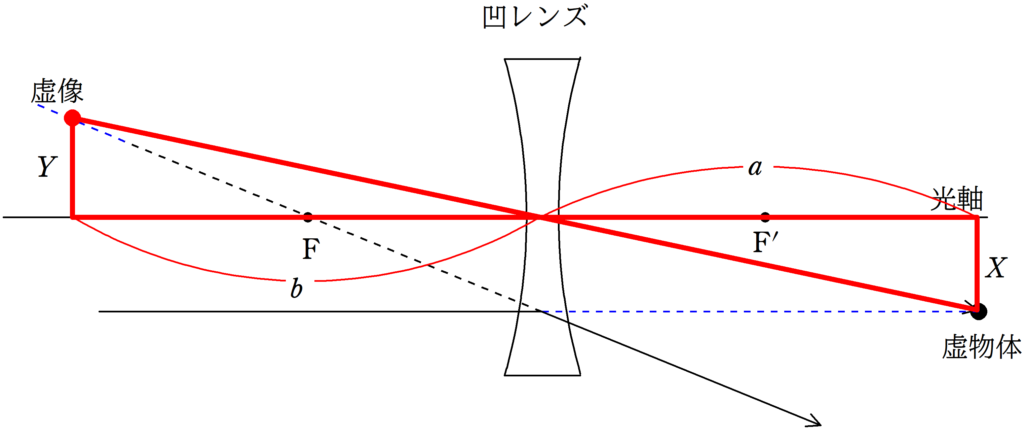
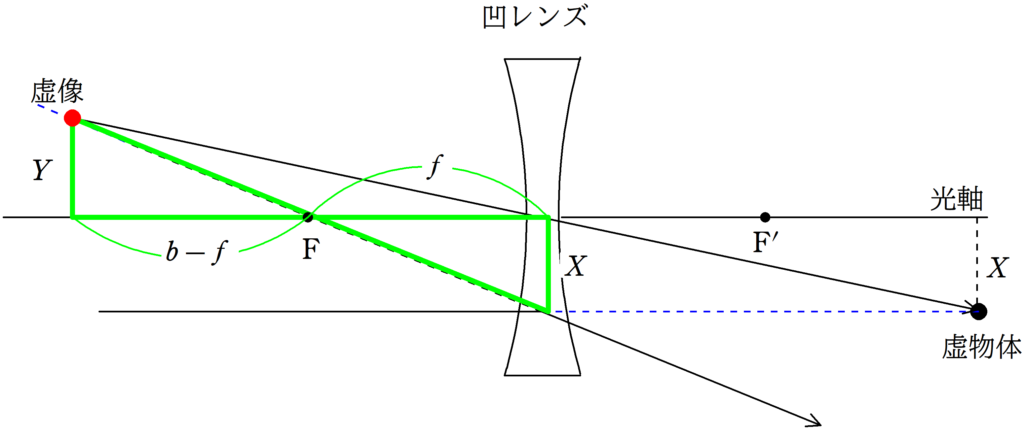
凸レンズと同様に，虚物体の高さを$X$，虚像の高さを$Y$として，2組の相似な図形を見つけ，相似比を考えます．

★　赤い方の相似比

$\dfrac{Y}{X}=\dfrac{b}{a}$　$\cdots　(3\ast)$

★　緑の方の相似比

$\dfrac{Y}{X}=\dfrac{b-f}{f}$　$\cdots　(4\ast)$

$(3\ast), (4\ast)$より

$\eqalign{\dfrac{b}{a}&=\dfrac{b-f}{f}\cr bf&=a(b-f)\cr bf=ab-af}$

両辺$abf$で割って

$\eqalign{\dfrac{1}{a}&=\dfrac{1}{f}-\dfrac{1}{b}\cr \dfrac{1}{a}+\dfrac{1}{b}&=\dfrac{1}{f}}$

NEKO

ここで，虚像が$b<0$，凹レンズで$f<0$であることとつじつまを合わせればいいんだね．

$-\dfrac{1}{a}-\dfrac{1}{b}=-\dfrac{1}{f}$　(答)

(3)　

NEKO

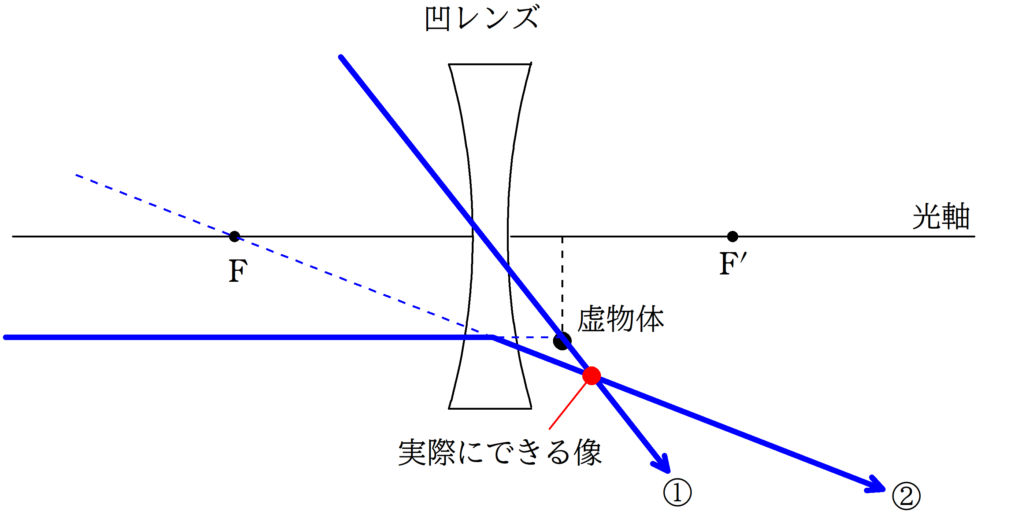
最後に，虚物体に向かう光線のうち，

①：平行光線

②：中心を通る光線

を作図します．

すると，赤い点に交点をもち，実像ができます．

同様に，虚物体の高さを$X$，虚像の高さを$Y$として，2組の相似な図形を見つけ，相似比を考えます．

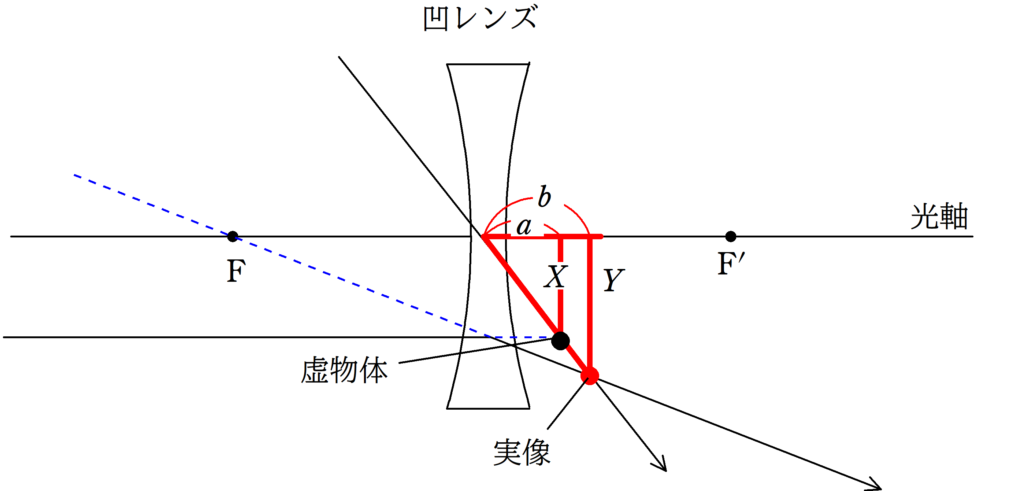
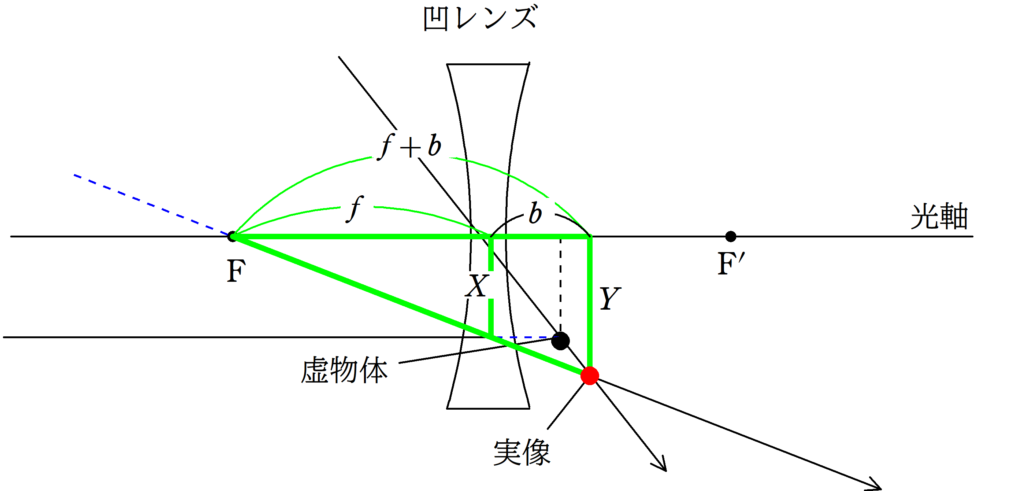
★　赤い方の相似比

$\dfrac{Y}{X}=\dfrac{b}{a}$　$\cdots　(5\ast)$

★　緑の方の相似比

$\dfrac{Y}{X}=\dfrac{f+b}{f}$　$\cdots　(6\ast)$

$(5\ast) , (6\ast)$より

$\eqalign{\dfrac{b}{a}&=\dfrac{f+b}{f}\cr bf&=a(f+b)\cr bf&=af+ab}$

両辺$abf$で割って

$\dfrac{1}{a}-\dfrac{1}{b}=\dfrac{1}{f}$

NEKO

実像で$b>0$であることと，凹レンズで$f<0$であることつじつまを合わせます．

$-\dfrac{1}{a}+\dfrac{1}{b}=-\dfrac{1}{f}$　(答)

NEKO

以上でおしまいます．

それでは，虚光源の場合も含めてレンズの式をまとめましょう！

レンズの式の統一（虚光源含みver.）

レンズと光源との距離を$|a|$，焦点距離を$|f|$，レンズと像との距離を$|b|$とする．

このとき，次の式が成り立つ．

$\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{f}$

ただし，次の規則で$a$と$b$と$f$の正負を決める．

$a>0　\dots$　実物体（実光源），　$a<0　\dots$　虚物体（虚光源）

$b>0　\dots$　実像，　$b<0　\dots$　虚像

$f>0　\dots$　，　凸レンズ　$f<0　\dots$　凹レンズ

PHYさん

次回の内容はこちらです．