
ロケットは燃料を逆噴射することで加速します.
噴射の際には,作用反作用の力のみがはたらくので,運動量が保存します.
この問題のポイントは次の2つです.
- 静止した人からみた速度を用いた運動量保存則を立てる.
- 問題文に与えられた燃料の噴射速度の条件をよく読む.
特に,後者はほとんどの場合次の問題の(1)ですが,まれに(2)や(3)のように書かれていることもあるので,その違いに注意をしてください.
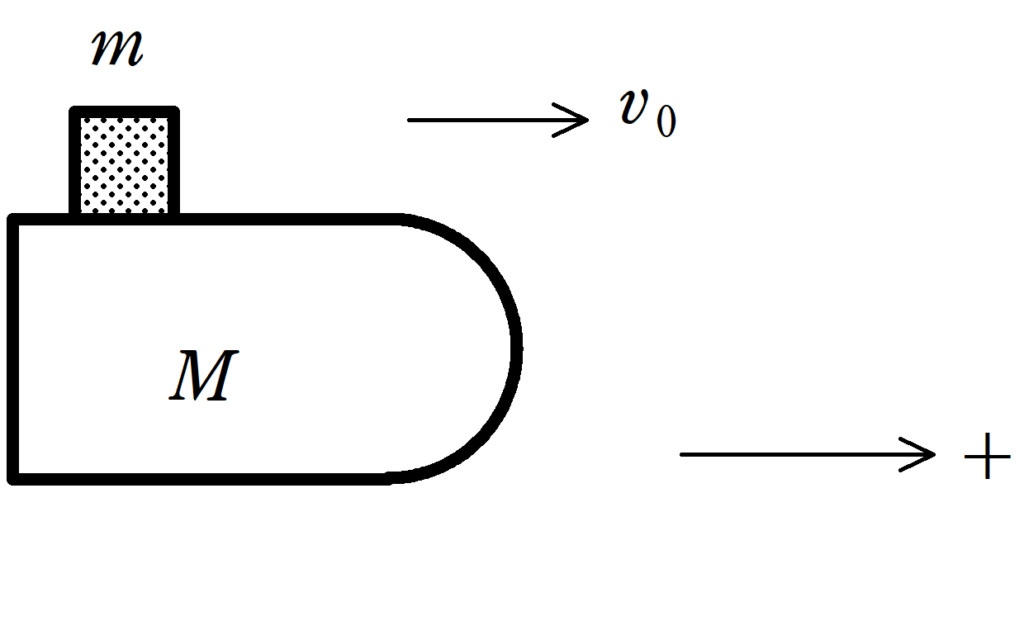
無重力空間中を一定の速度$v_{0}$で進んでいるロケットがある.このロケットには質量$m$の燃料を積んでおり,燃料を除くロケットの質量は$M$である.ロケットは燃料を速度の向きと逆向きに噴射し,加速する.以下,ロケットの速度の向きを正とし,次の3通りの噴射方法における加速後のロケットの速度を求めよ.ただし,燃料の噴射時間は十分短いとする.
(1) 噴射前のロケットの速度に対して,速さ$v_{1}$で燃料をすべて噴射した後のロケットの速度$V_{1}$を求めよ.
(2) 噴射前のロケットの速度に対して,速度$v_{2}$で燃料をすべて噴射した後のロケットの速度$V_{2}$を求めよ.
(3) 噴射後のロケットの速度に対して,速さ$v_{3}$で燃料をすべて噴射した後のロケットの速度$V_{3}$を求めよ.
<解答>
(1)

(1)では,燃料を噴射前のロケットの速度に対して速さ$v_{1}$で噴射しています.
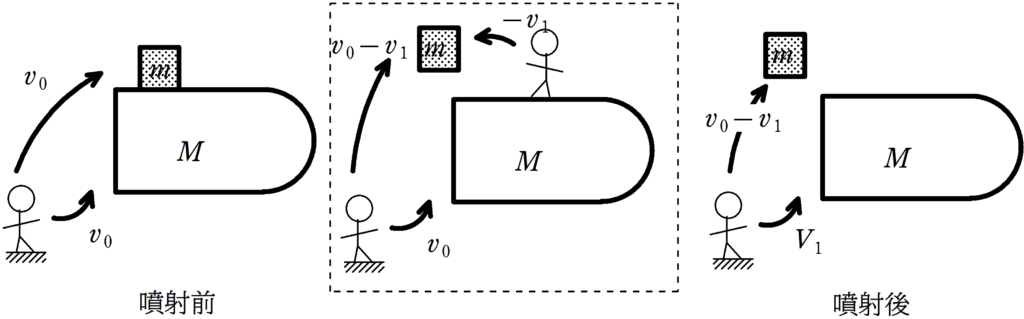
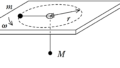
つまり,下図の点線で囲まれたように,ロケットの速度$v_{0}$からみたときの燃料の速度は$-v_{1}$となります.
さらに,これを静止した人からみると,その速度は$v_{0}-v_{1}$となります.
★ 運動量保存則
$(M+m)v_{0}=MV_{1}+m(v_{0}-v_{1})$
$\therefore V_{1}=v_{0}+\dfrac{m}{M}v_{1}$ (答)
(2)

今度は速度が与えられています.
噴射前のロケットの速度に対して,速度$v_{2}$で燃料を噴射しているので,これを静止している人からみると,その速度は$v_{0}+v_{2}$となります.

★ 運動量保存則
$(M+m)v_{0}=MV_{2}+m(v_{0}+v_{2})$
$\therefore V_{2}=v_{0}-\dfrac{m}{M}v_{2}$ (答)
(3)

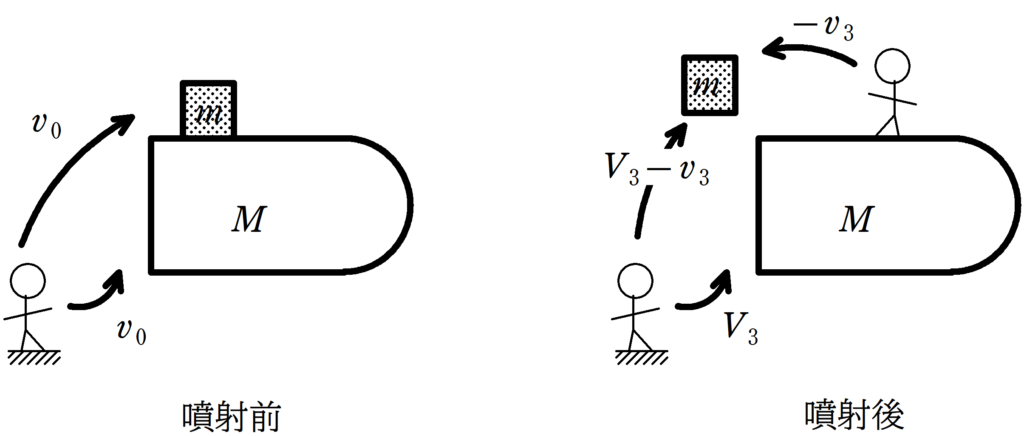
最後は,噴射後のロケットの速度に対して,速さ$v_{3}$で噴射しています.速度を考えれば,$-v_{3}$ですね.
なので,静止しているからみると,燃料の速度は$V_{3}-v_{3}$となります.
★ 運動量保存則
$(M+m)v_{0}=MV_{3}+m(V_{3}-v_{3})$
$\therefore V_{2}=v_{0}+\dfrac{m}{M+m}v_{3}$ (答)

3つの微妙な問題文の違いに注意をしましょう.

コメント