
今回は,「面積速度一定則」を使う演習問題です.
「面積速度一定則」の確認したうえで問題を解いてみましょう.
$\rm O$を中心として物体が運動しているときを考える.
物体の軌道面と平行な力が中心$\rm O$(または中心軸)を向くとき,面積速度$\dfrac{\varDelta S}{\varDelta t}$が一定となる.
面積速度は中心$\rm O$と物体を結ぶ線分が単位時間あたりに通過する面積である.
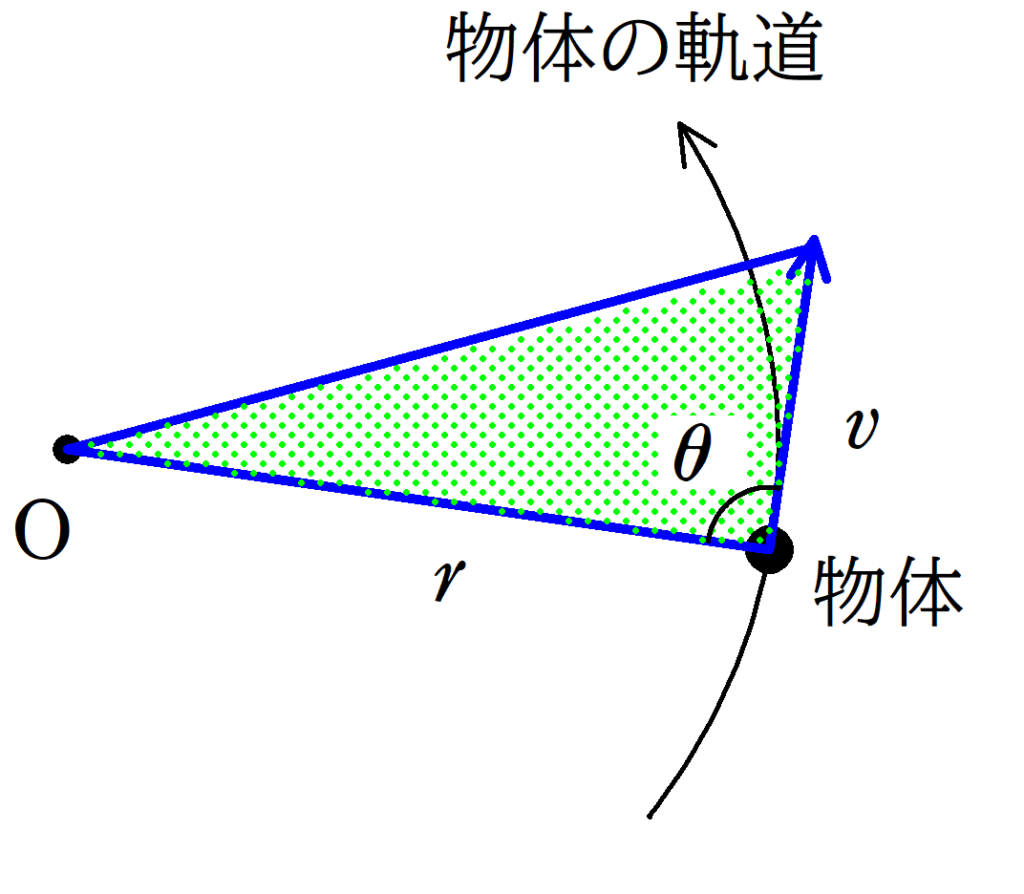
上図のように,$\rm O$と物体の距離が$r$,物体の速さを$v$,$\rm O$と物体を結ぶ線分と速度とのなす角を$\theta$とすると,面積速度は
$\dfrac{\varDelta S}{\varDelta t}=\dfrac{1}{2}rv\sin\theta$
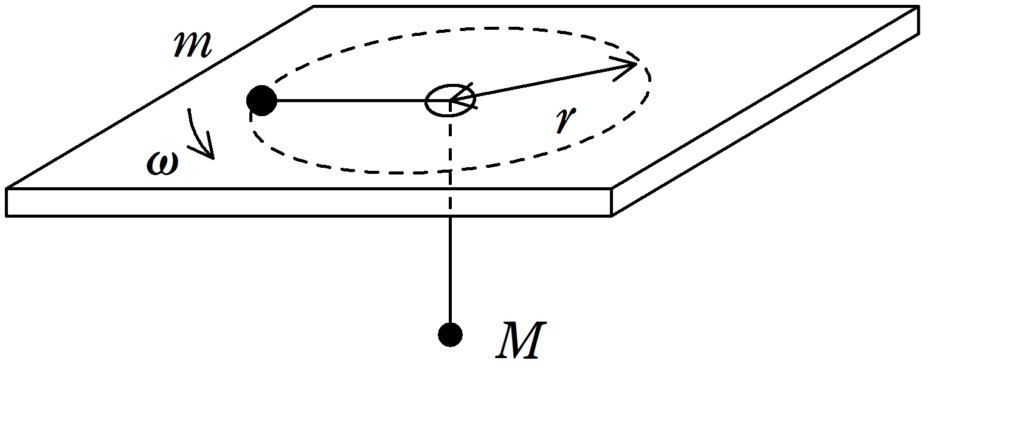
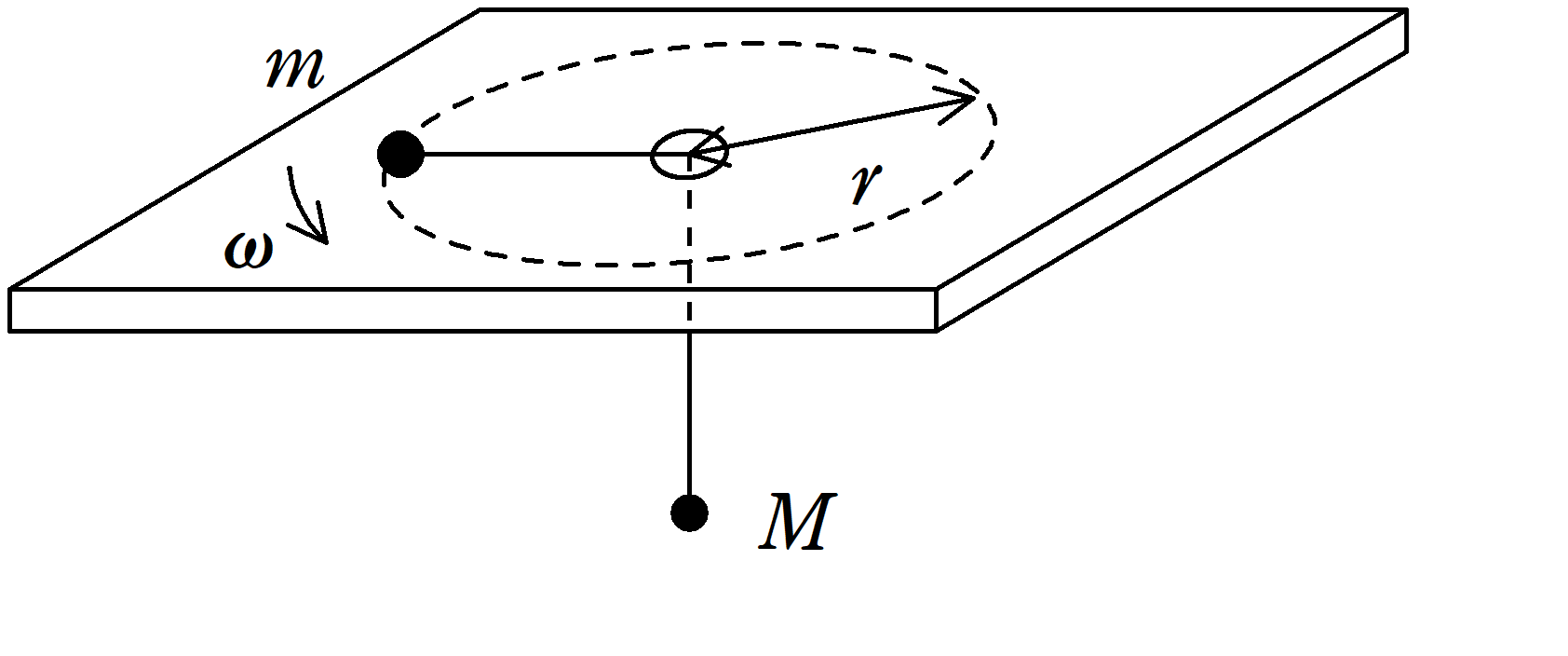
図のように,伸び縮みしない軽い糸で結ばれた質量$m$の質点が,摩擦のない水平な板の上で半径$r$,角速度$\omega$の等速円運動をしている.糸は板の中央に開けられた十分小さい穴を通して下方に垂れ下がり,他端に質量$M$の物体が取りつけられている.重力加速度の大きさを$g$として次の問いに答えよ.
(1) 半径$r$の等速円運動をしているとき,$\omega$を$m$,$M$,$r$,$g$を用いて表せ.
(2) (1)の状態から,物体にゆっくりと力を加え,質点の円運動の半径を$r$から,$r-\varDelta r$にした.それと同時に質点の角速度も$\omega+\varDelta \omega$に変化した.このとき,面積速度一定則を用いて,$\varDelta \omega$を$\varDelta r$,$r$,$\omega$を用いて表せ.ただし,$\varDelta \omega$,$\varDelta r$は十分小さく,次の近似式が成り立つとしてよい.
$(\varDelta r)^{2}\fallingdotseq 0$,$\varDelta \omega \cdot \varDelta r\fallingdotseq 0$
<解答>
(1)

物体のつり合いから張力の大きさは,$Mg$です.質点の向心方向の運動方程式を立てると,次のようになります.
半径$r$,円運動の接線方向の速さを$v$,角速度を$\omega$とすると,向心加速度の大きさ$a$は
$a=\dfrac{v^{2}}{r}=r\omega^{2}$
向心加速度の向きは円運動の中心
★ 運動方程式
$mr\omega^{2}=Mg$
$\therefore \omega=\sqrt{\dfrac{Mg}{mr}}$ (答)
(2)

次の面積速度一定則を立てます.
面積速度$A$は
$A=\dfrac{1}{2}rv$
ですが,今回は角速度$\omega$を使います.
円運動における速さ$v$と角速度$\omega$の関係は
$v=r\omega$
なので,面積速度$A$は
$\eqalign{A&=\dfrac{1}{2}rv\\&=\dfrac{1}{2}r\cdot r\omega\\&=\dfrac{1}{2}r^{2}\omega}$
と変形します.
★ 面積速度一定則
$\eqalign{\dfrac{1}{2}r^{2}\omega&=\dfrac{1}{2}(r-\varDelta r)^{2}(\omega+\varDelta \omega)\\&\fallingdotseq \dfrac{1}{2}(r^{2}-2r\varDelta r)(\omega+\varDelta \omega)\\&\fallingdotseq \dfrac{1}{2}r^{2}\omega+\dfrac{1}{2}r^{2}\varDelta \omega-r\omega\varDelta r}$
したがって,$\varDelta \omega=\dfrac{2\varDelta r}{r}\omega$ (答)


コメント
[…] […]