
前回同様,面積速度一定則の問題です.
$\rm O$を中心として物体が運動しているときを考える.
物体の軌道面と平行な力が中心$\rm O$(または中心軸)を向くとき,面積速度$\dfrac{\varDelta S}{\varDelta t}$が一定となる.
面積速度は中心$\rm O$と物体を結ぶ線分が単位時間あたりに通過する面積である.
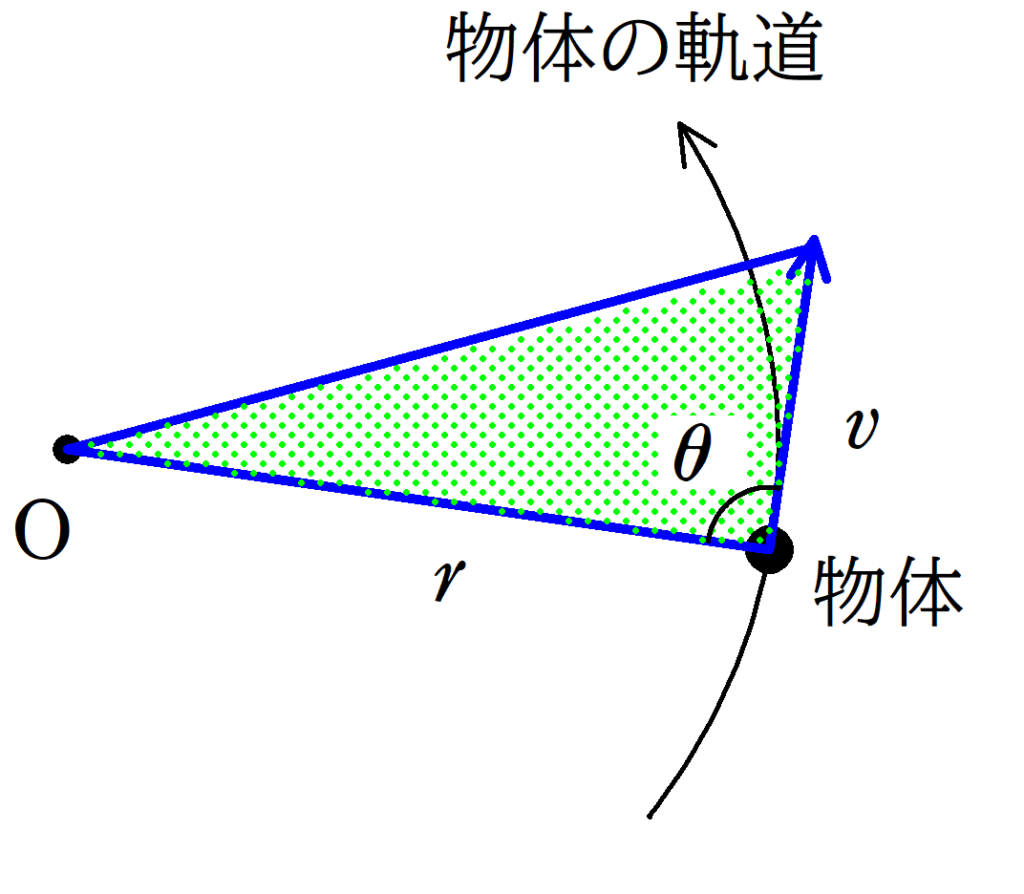
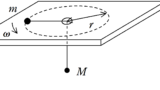
上図のように,$\rm O$と物体の距離が$r$,物体の速さを$v$,$\rm O$と物体を結ぶ線分と速度とのなす角を$\theta$とすると,面積速度は
$\dfrac{\varDelta S}{\varDelta t}=\dfrac{1}{2}rv\sin\theta$
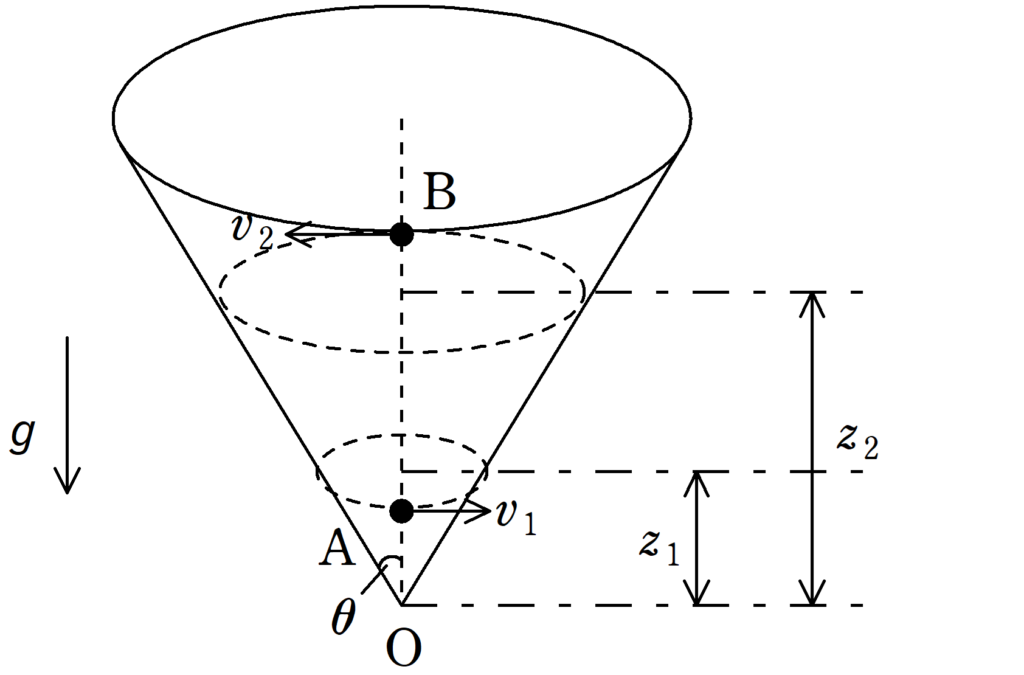
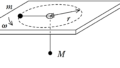
図のように,直円錐型容器の内側の面に沿った質量$m$の小球の運動について考える.ただし,容器の面はなめらかであり,小球の大きさおよび容器の厚さは無視できるものとする.また,円錐の軸は鉛直線と平行であり,円錐の半頂角は$\theta$である.円錐の頂点をOとし,重力加速度の大きさを$g$とする.
Oより高さ$z_{1}$の点Aにおいて,容器の面に沿って水平方向に小球を速さ$v_{1}$で打ち出したところ,小球は面に沿って運動しながら上昇し,Oより高さ$z_{2}$の点Bにおいて高さが最大となり,そのときの速さが$v_{2}$であった.このとき,次の問いに答えよ.
(1) AとBにおいて,面積速度一定則を立てよ.
(2) AとBにおいて,力学的エネルギー保存則を立てよ.
(3) (1),(2)より,$v_{1}$,$v_{2}$を$z_{1}$,$z_{2}$,$g$を用いて表せ.
<解答>
(1)
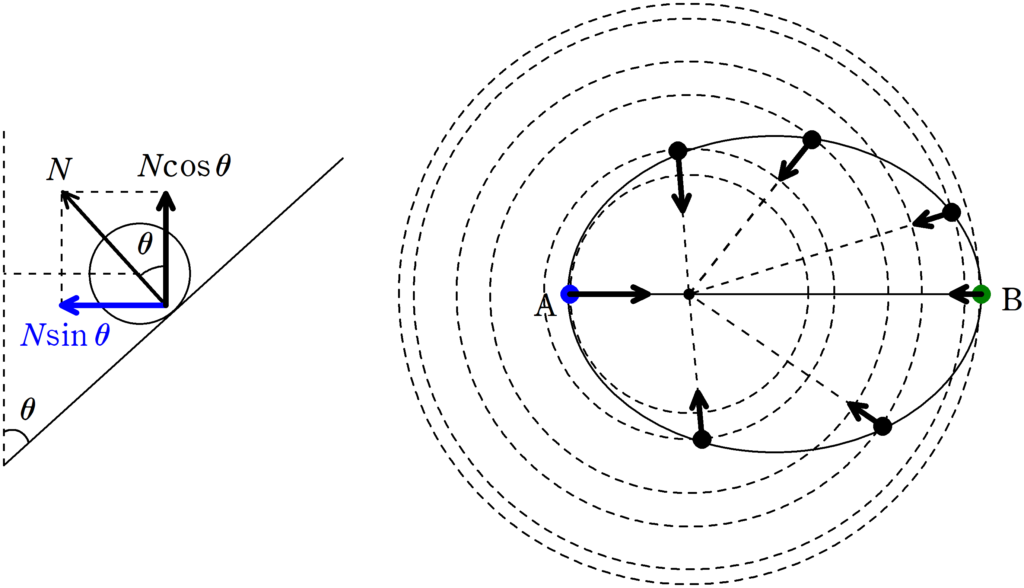

小球にはたらく力は垂直抗力と重力です.
このとき,垂直抗力の水平成分は常に円錐の中心軸に向かいます.
垂直抗力抗力の大きさを$N$とすると,中心軸に向かう成分は$N\sin\theta$となります.
小球の運動を鉛直真上からみると上右図のようになります.
常に中心軸に力がはたらくので,面積速度一定則が成り立ちます.
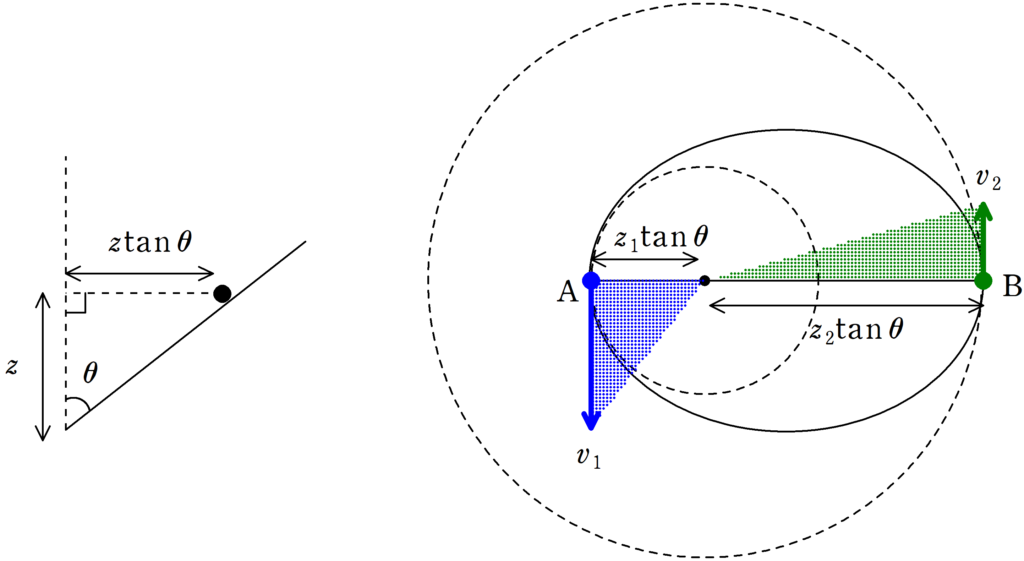

高さが$z$における中心軸からの距離は$z\tan\theta$となります.
AとBの間で面積速度一定則を立てましょう.
面積速度は右上図の色塗り部分です.
★ 面積速度一定則
$\dfrac{1}{2}z_{1}\tan\theta v_{1}=\dfrac{1}{2}z_{2}\tan \theta v_{2}$ (答)
$\therefore v_{2}=\dfrac{z_{1}}{z_{2}}v_{1}$ $\dots (\ast)$
(2)

さらに,力学的エネルギー保存則を立てます.
★ 力学的エネルギー保存則
$\dfrac{1}{2}mv_{1}^{2}+mgz_{1}=\dfrac{1}{2}mv_{2}^{2}+mgz_{2}$ (答)
$\therefore v_{1}^{2}-v_{2}^{2}=2g(z_{2}-z_{1})$ $(2\ast)$
(3)

$(\ast)$と$(2\ast)$から$v_{1}$,$v_{2}$を求めましょう.
$(\ast)$を$(2\ast)$に代入して
$\eqalign{v_{1}^{2}-\dfrac{z_{1}^{2}}{z_{2}^{2}}v_{1}^{2}&=2g(z_{2}-z_{1})\cr \dfrac{(z_{2}+z_{1})\cancel{(z_{2}-z_{1})}}{z_{2}^{2}}v_{1}^{2}&=2g\cancel{(z_{2}-z_{1})}\cr v_{1}&=z_{2}\sqrt{\dfrac{2g}{z_{1}+z_{2}}}}$
さらに,$(\ast)$より,$v_{2}=z_{1}\sqrt{\dfrac{2g}{z_{1}+z_{2}}}$

ということで,
$v_{1}=z_{2}\sqrt{\dfrac{2g}{z_{1}+z_{2}}}$ (答)
$v_{2}=z_{1}\sqrt{\dfrac{2g}{z_{1}+z_{2}}}$ (答)




コメント