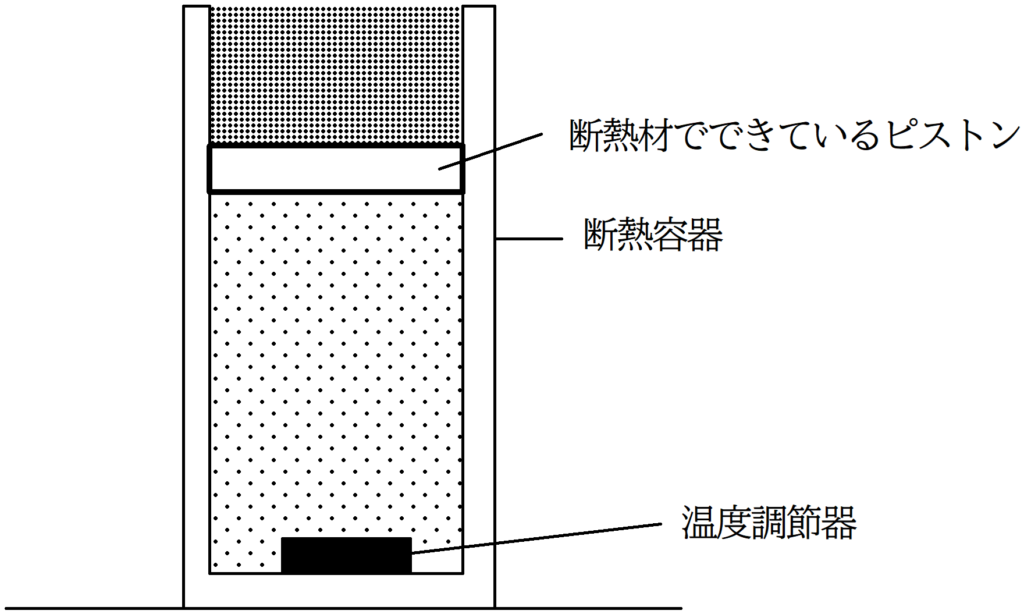
図のように,水平な床の上に,高さ$2h$の厚さの無視できる容器が置かれており,断面積$S$の質量の無視できるピストンによって,単原子分子理想気体が密封されている.ピストンは自由に動くことができる.また,容器,ピストンともに,断熱材によってできていて,容器内の気体は温度調節器によって,温度を調節できる.重力加速度の大きさを$g$,大気圧を$p_{0}$として次の問いに答えよ.
まず,ピストンの上に密度$\rho$の液体を容器いっぱいになるまでゆっくりと注いだところ,ピストンは容器の底面から高さ$h$の場所に静止した.(状態I)
(1) 状態Iの気体の圧力$p_{1}$を求めよ.
次に,状態Iから温度調節器を使うと,ピストンはゆっくりと上昇し,液体は容器からこぼれおち,ピストンの高さが$2h$になると,液体はすべてなくなった.
(2) ピストンの高さが$x(h\leqq x\leqq 2h)$における気体の圧力$p_{x}$と体積$V_{x}$の関係を求め,$pV$図完成させよ.ただし,$p_{0}=\rho hg$として,$p_{0}$,$S$,$h$を用いよ.
(3) (2)のとき,ピストンが動き始めてから,ピストンの高さが$x(h\leqq x\leqq 2h)$までに,気体がした仕事$W_{x}$, 内部エネルギー変化$\varDelta U_{x}$,気体が吸収する熱量$Q_{x}$をそれぞれ求めよ.
(4) (3)を利用して,準静的変化を維持するために吸収から放熱に移り変わる位置$x$を求めよ.
<解答>

熱力学の問題で意識をして立てて欲しいのは,次の3つの式です.
- 可動部分のつり合いの式 → 力の情報が出てくる
- 理想気体の状態方程式(ボイルシャルルの法則)
- 熱力学第一法則 → エネルギーの情報が出てくる
(1)

ピストンのつり合いの式を立てましょう.
容器内部の気体がおす力が$p_{1}S$です.
液体の高さは$h$なので,液体の体積は$Sh$です.液体の密度が$\rho$なので,液体の質量は$\rho Sh$なので,重さは$\rho Shg$となります.
また,大気が液体を通して押す力は$p_{0}S$です.
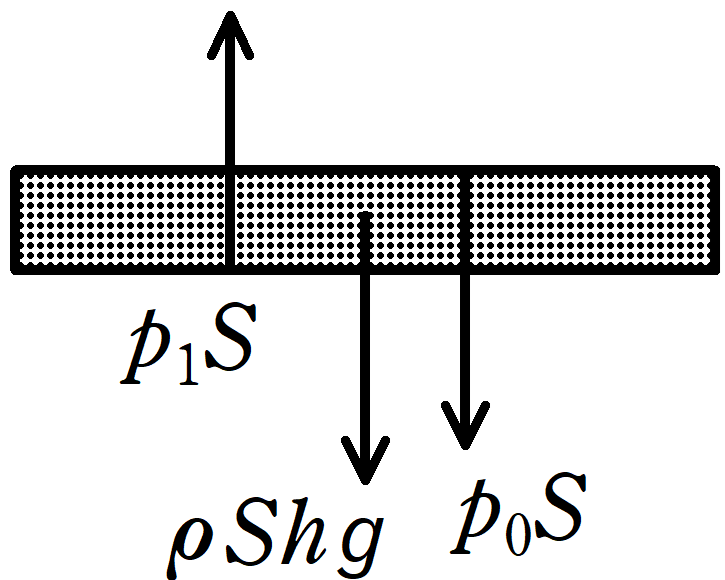
★ つり合いの式
$p_{1}S=p_{0}S+\rho Shg$
$\therefore p_{1}=p_{0}+\rho hg$ (答)
(2)

ピストンの高さが$x$のとき,液体の高さは$2h-x$になるので,その重さは$\rho S(2h-x)g$です.
再びつり合いの式を立てましょう.

★ つり合いの式
$p_{x}S=p_{0}S+\rho S(2h-x)g$\\
$\therefore p_{x}=p_{0}+2\rho hg-\rho xg$
また,問題の条件である,$p_{0}=\rho hg$と$\rho g=\dfrac{p_{0}}{h}$を代入しましょう.
$p_{x}=3p_{0}-\dfrac{p_{0}}{h}x$
$V_{x}=Sx$より,$x=\dfrac{V_{x}}{S}$を上式に代入すると
$p_{x}=3p_{0}-\dfrac{p_{0}}{Sh}V_{x}$ $\dots (\ast)$

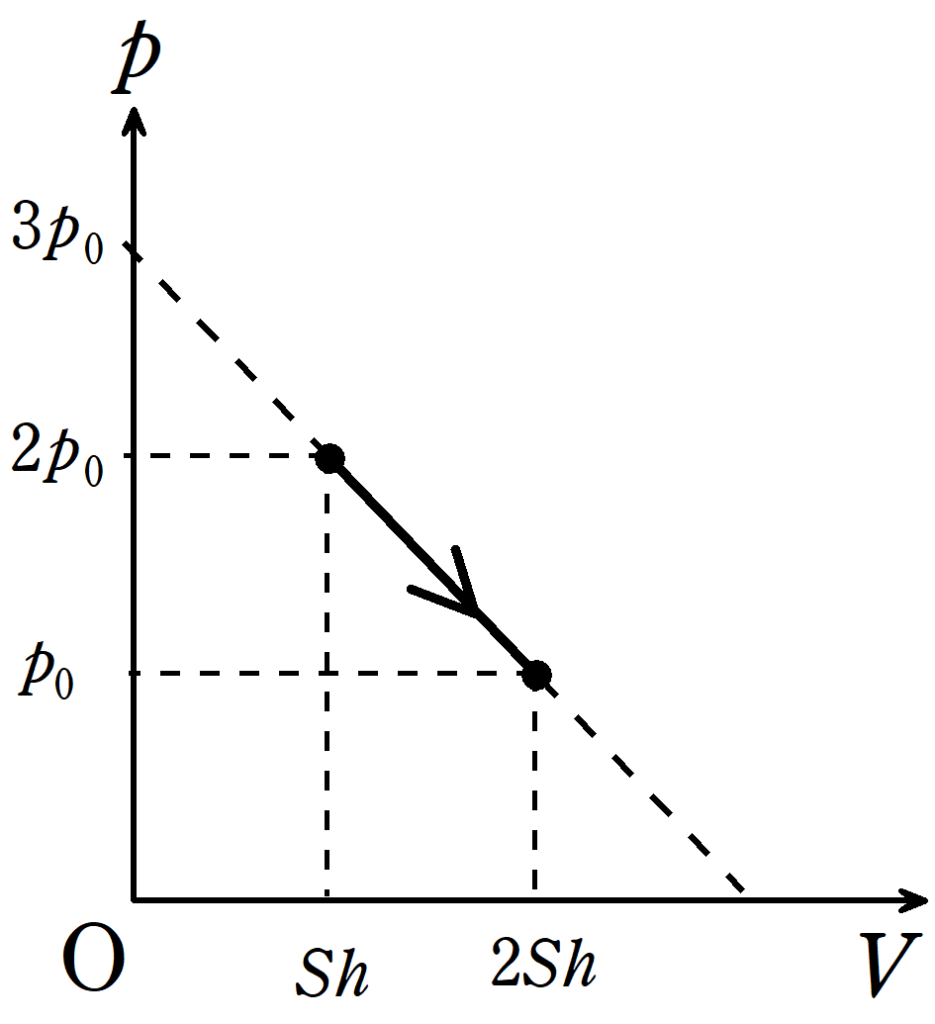
$(\ast)$より,体積が$Sh$のとき,圧力は$2p_{0}$になり,体積が$2Sh$のときは,圧力は$p_{0}$です.
したがって,$pV$図は下のようになります.
(3)

$pV$図の面積を求めることで気体がする仕事を計算できます.
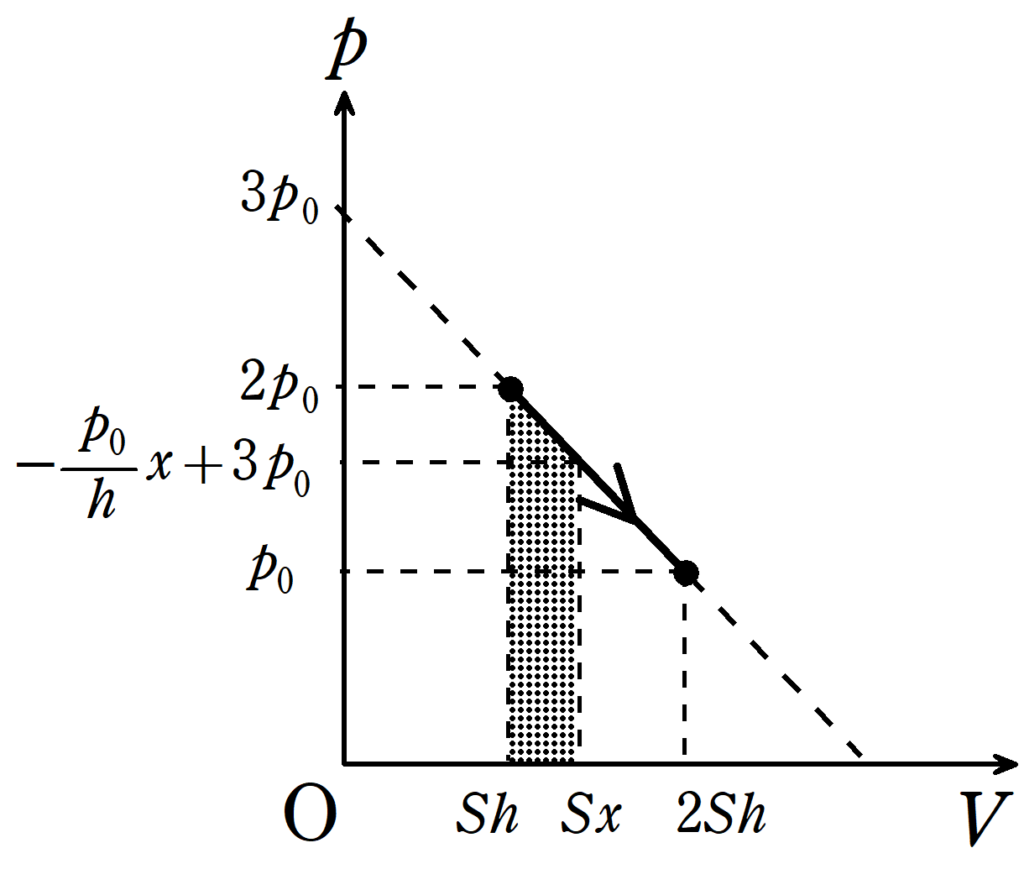
$(\ast)$において,再び$V_{x}=Sx$とすると,
$p_{x}=-\dfrac{p_{0}}{h}x+3p_{0}$
上図の台形の面積は
$\eqalign{W_{x}&=\dfrac{1}{2}\cdot \left(-\dfrac{p_{0}}{h}x+3p_{0}+2p_{0}\right)\cdot S(x-h)\\&=-\dfrac{p_{0}S}{2h}x^{2}+3p_{0}Sx-\dfrac{5}{2}p_{0}Sh}$ (答)
問題分に単原子分子理想気体とかいてあるときは,次のことを使うことができる.
定積モル比熱が$\dfrac{3}{2}R$である.すなわち
内部エネルギー$U$は
$U=\dfrac{3}{2}nRT=\dfrac{3}{2}pV$
内部エネルギーの変化$\Delta U$は
$\Delta U=\dfrac{3}{2}nR\Delta T=\dfrac{3}{2}(p_{2}V_{2}-p_{1}V{1})$
※$n$:物質量,$T$:絶対温度,$p$:圧力,$V$:体積
★ 内部エネルギーの式
$\eqalign{\varDelta U_{x}&=\dfrac{3}{2}\left\{\left(-\dfrac{p_{0}}{h}x+3p_{0}\right)Sx-2p_{0}Sh\right\}\\&=-\dfrac{3p_{0}S}{2h}x^{2}+\dfrac{9}{2}p_{0}Sx-3p_{0}Sh}$ (答)
内部エネルギーの変化を$\Delta U$,気体が吸収する熱量を$Q$,気体がした仕事を$W$とすると
$Q=\Delta U+W$
★ 熱力学第一法則
$\eqalign{Q_{x}&=\varDelta U_{x}+W_{x}\\&=-\dfrac{3p_{0}S}{2h}x^{2}+\dfrac{9}{2}p_{0}Sx-3p_{0}Sh-\dfrac{p_{0}S}{2h}x^{2}+3p_{0}Sx-\dfrac{5}{2}p_{0}Sh\\&=-\dfrac{2p_{0}S}{h}x^{2}+\dfrac{15}{2}p_{0}Sx-\dfrac{11}{2}p_{0}Sh}$ (答)
(4)

(3)で得た$Q_{x}$の式を平方完成すると次のようになります.
$Q_{x}=-\dfrac{2p_{0}S}{h}\left(x-\dfrac{15}{8}h\right)^{2}+\dfrac{49}{32}p_{0}Sh$

縦軸を$Q_{x}$,横軸を$x$としたグラフをかくと次のようになります.
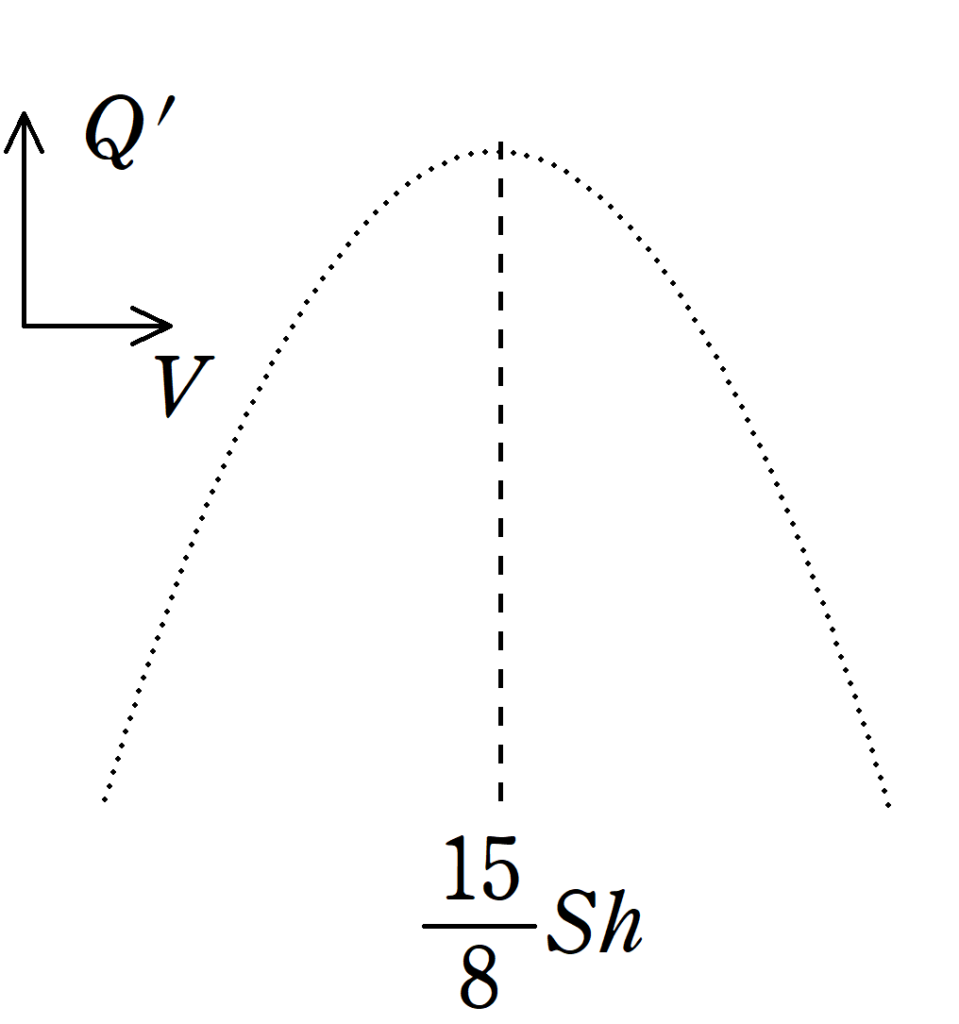

$x=h$から$x=\dfrac{15}{8}h$までは吸収した熱量が増え続けていますが,$x=\dfrac{15}{8}h$を境に減っています.
したがって,$x=\dfrac{15}{8}h$を境に吸収から放熱に変化しています.(答)


コメント