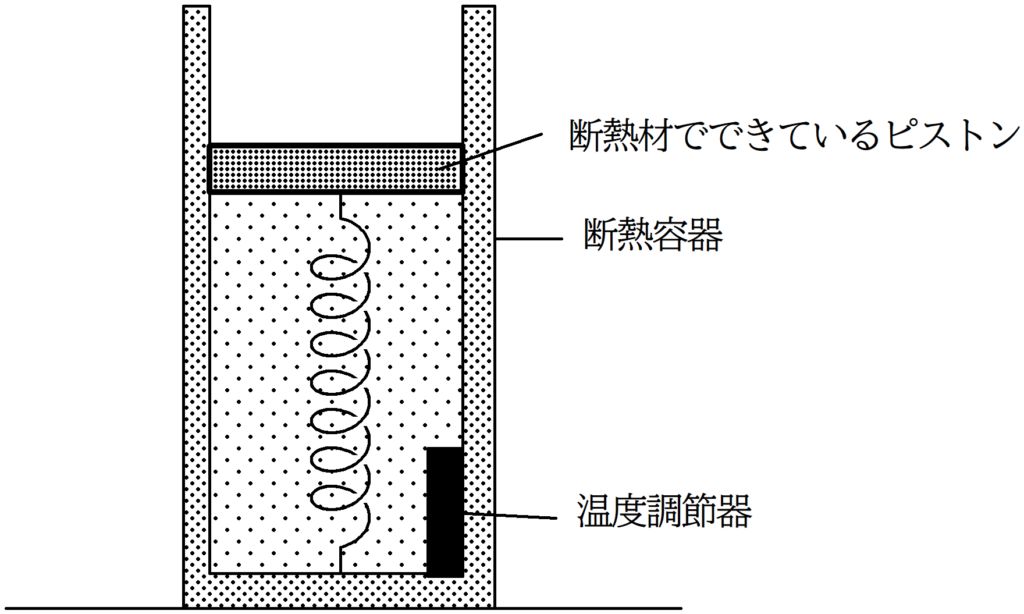
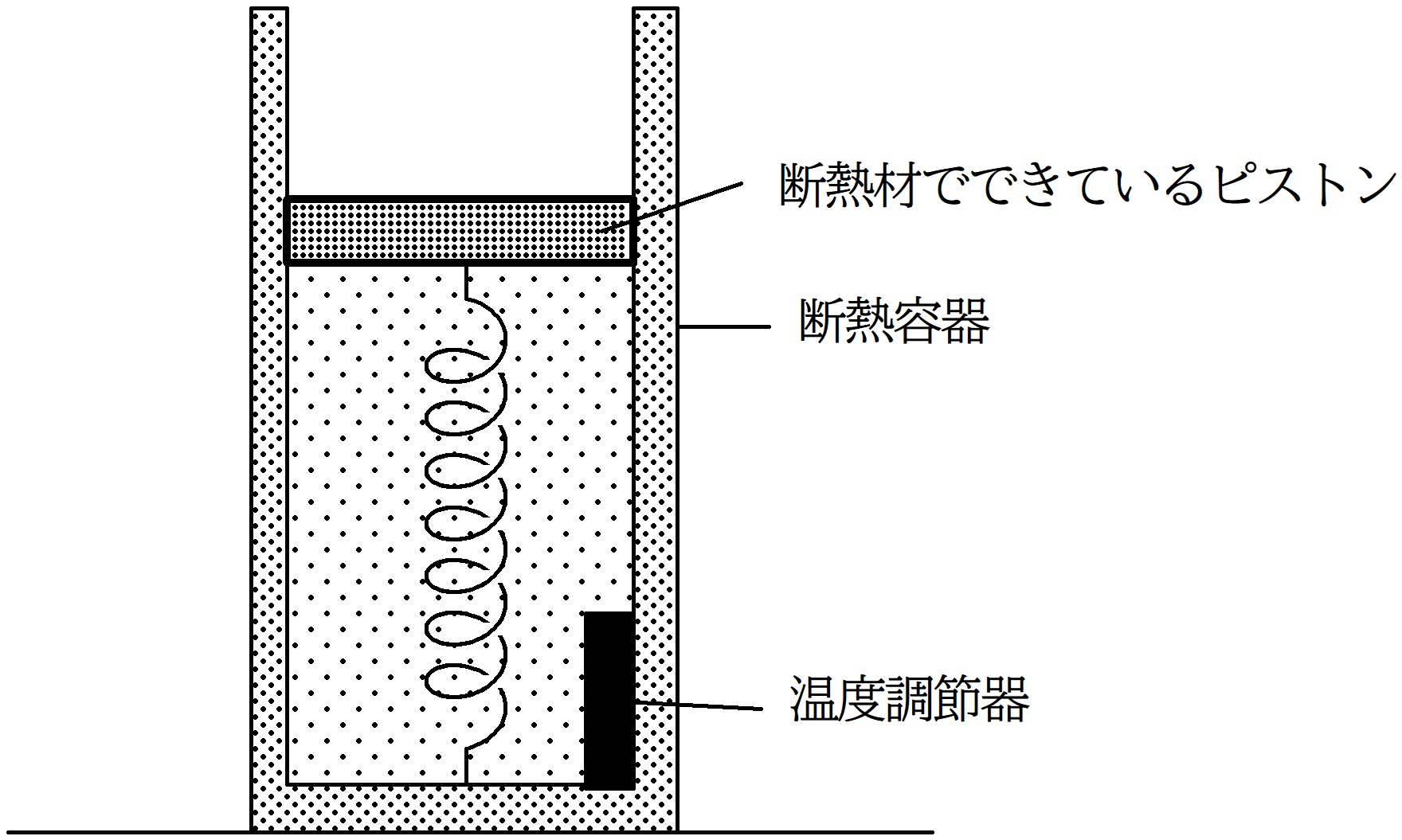
図のように,水平な床の上に,容器が置かれており,断面積$S$,質量$m$のピストンによって,単原子分子理想気体が密封されている.ピストンはなめらかに動くことができる.また,容器,ピストンともに,断熱材によってできていて,容器内の気体は温度調節器によって温度を調節できる.重力加速度の大きさを$g$,大気圧を$p_{0}$として次の問いに答えよ.
ばね定数$k$のばねをピストン下面と容器底面に取りつけたところ,ちょうどばねは自然長$h$となってピストンがつりあっていた.(状態I)
(1) このときの圧力を求めよ.
次に,温度調節器によって,内部の気体をあたためたところ,ピストンは容器の底面より高さ$\dfrac{3}{2}h$の場所まで移動した.(状態II)
(2) ピストンが容器の底面より高さ$x\left(h\leqq x\leqq \dfrac{3}{2}h\right)$にあるときのつり合いの式を立て,状態Iから状態IIに変化する間の$pV$図をかけ.
(3) 状態Iから状態IIの間に気体がした仕事$W$,内部エネルギー変化の変化$\varDelta U$,気体が吸収した熱量$Q$をそれぞれ求めよ.
<解答>

熱力学の問題で意識をして立てて欲しいのは,次の3つの式です.
- 可動部分のつり合いの式 → 力の情報が出てくる
- 理想気体の状態方程式(ボイルシャルルの法則)
- 熱力学第一法則 → エネルギーの情報が出てくる
(1)

気体の圧力を$p_{1}$として,ピストンのつり合いの式を立てましょう.
まずは,ピストンの重力.
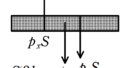
そして,内部の気体が押す力は鉛直上向きに$p_{1}S$です.
外の空気は鉛直下向きに$p_{0}S$の力で押しています.
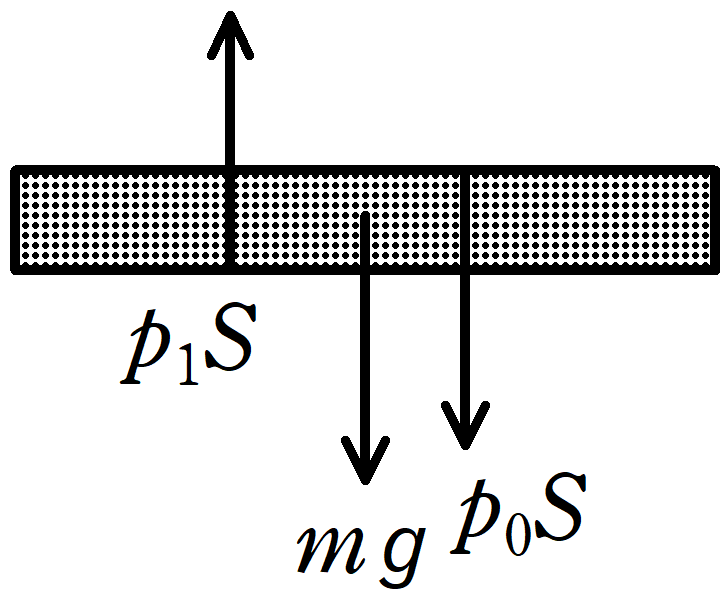
★ ピストンのつり合い
$p_{1}S=p_{0}S+mg$
$\therefore p_{1}=p_{0}+\dfrac{mg}{S}$ (答)
(2)

高さ$x$における圧力を$p_{x}$,体積を$V_{x}$として$p_{x}$と$V_{x}$の関係を調べます.
そのために,ピストンが高さ$x$にあるときのつり合いの式を立てます.
容器内の気体が押す力とピストンの重力,外の空気が押す力以外に,弾性力がはたらきます.
自然長からの伸びが$x-h$なので,弾性力の大きさは$k(x-h)$です.
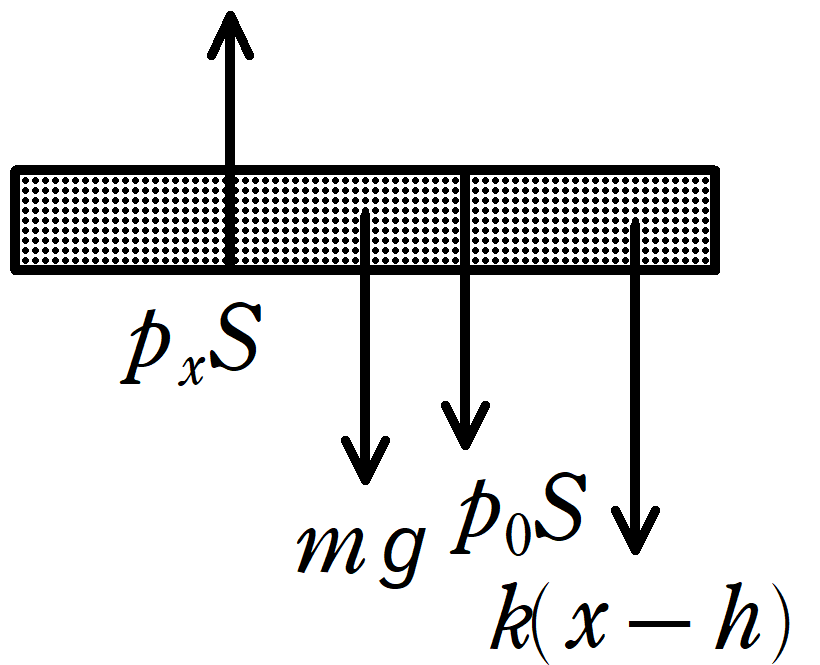
★ つり合いの式
$p_{x}S=p_{0}S+mg+k(x-h)$
$\therefore p_{x}=p_{0}+\dfrac{mg}{S}+\dfrac{k}{S}(x-h)$ $\dots (\ast)$

また,$(\ast)$より,$x=\dfrac{3}{2}h$における圧力$p_{2}$は
$p_{2}=p_{0}+\dfrac{mg}{S}+\dfrac{kh}{2S}$

また,ピストンが高さ$x$にあるときの体積$V_{x}$は,$V_{x}=Sx$なので,$x=\dfrac{V(x)}{S}$なので$(\ast)$より次のようになります.
$\eqalign{p_{x}&=p_{0}+\dfrac{mg}{S}+\dfrac{k}{S}\left(\dfrac{V_{x}}{S}-h \right)\\&=\dfrac{k}{S^{2}}V_{x}+p_{0}+\dfrac{mg}{S}-\dfrac{kh}{S}}$ (答)

$p_{x}$$=\dfrac{k}{S^{2}}$$V_{x}$$+p_{0}+\dfrac{mg}{S}-\dfrac{kh}{S}$
なので,縦軸を圧力,横軸を体積とした$pV$図は正の傾きである直線です.
次のようなグラフになります.
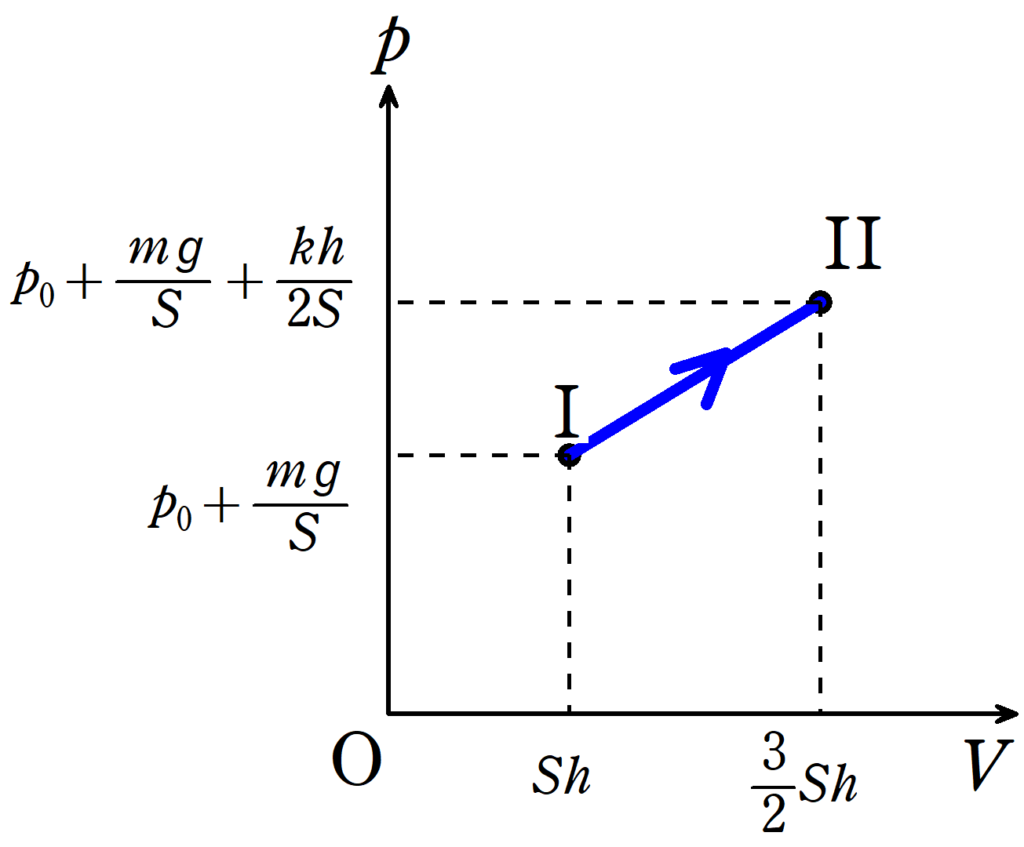
(3)

気体がする仕事$W$は$pV$図の面積で求めます.
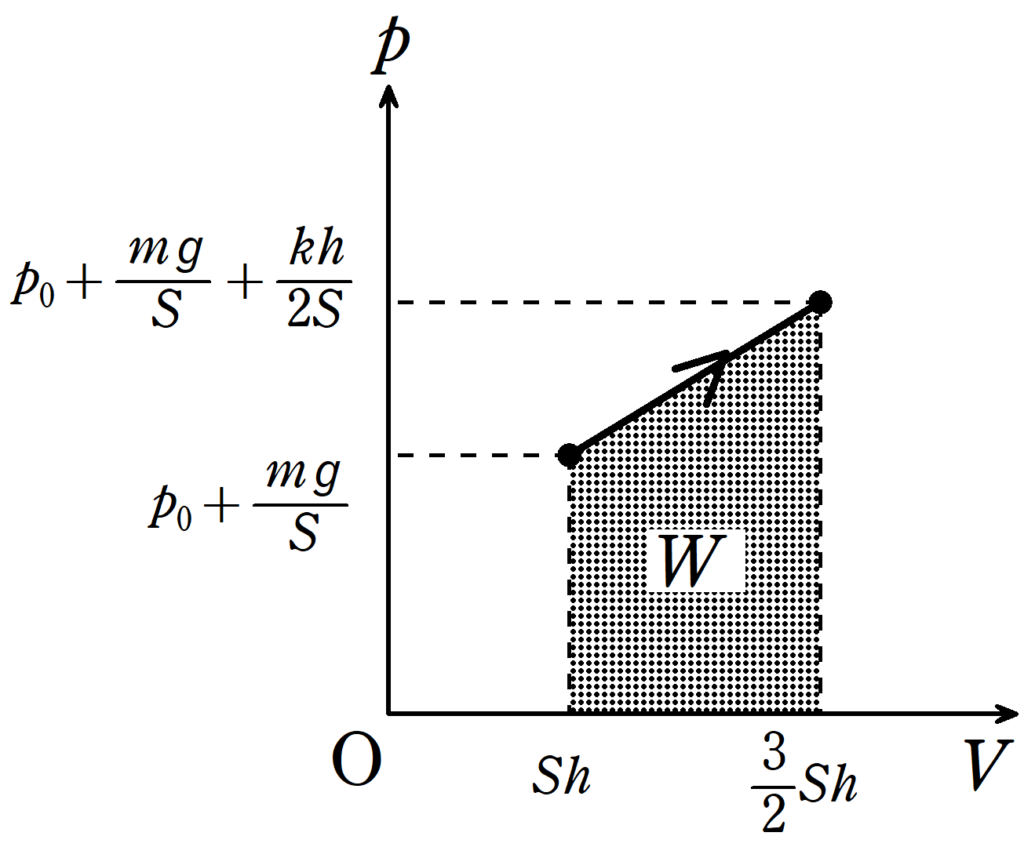
$\eqalign{W&=\dfrac{1}{2}\cdot \left(p_{0}+\dfrac{mg}{S}+p_{0}+\dfrac{mg}{S}+\dfrac{kh}{2S}\right)\cdot \left(\dfrac{3}{2}Sh-Sh\right)\\&=\dfrac{1}{2}p_{0}Sh+\dfrac{1}{2}mgh+\dfrac{1}{8}kh^{2}}$

これは,ピストンの力学的エネルギー変化と非保存力がした仕事の関係からも求めることができます.
重力の位置エネルギー変化と弾性力がする仕事の変化の和が大気圧がした負の仕事と気体がする仕事の和と等しいという式を立てます.
★ 力学的エネルギー変化=非保存力がした仕事
$mg\cdot \dfrac{1}{2}h+\dfrac{1}{2}k\cdot\left(\dfrac{1}{2}h\right)^{2}=W+\left(-p_{0}S\cdot \dfrac{h}{2}\right)$\\
$\therefore W=\dfrac{1}{2}p_{0}Sh+\dfrac{1}{2}mgh+\dfrac{1}{8}kh^{2}$
問題分に単原子分子理想気体とかいてあるときは,次のことを使うことができる.
定積モル比熱が$\dfrac{3}{2}R$である.すなわち
内部エネルギー$U$は
$U=\dfrac{3}{2}nRT=\dfrac{3}{2}pV$
内部エネルギーの変化$\Delta U$は
$\Delta U=\dfrac{3}{2}nR\Delta T=\dfrac{3}{2}(p_{2}V_{2}-p_{1}V{1})$
※$n$:物質量,$T$:絶対温度,$p$:圧力,$V$:体積
★ 内部エネルギー変化の式
$\eqalign{\varDelta U&=\dfrac{3}{2}\left\{\left(p_{0}+\dfrac{mg}{S}+\dfrac{kh}{2S}\right)\cdot \dfrac{3}{2}Sh-\left(p_{0}+\dfrac{mg}{S}\right)\cdot Sh\right\}\\&=\dfrac{3}{4}p_{0}Sh+\dfrac{3}{4}mgh+\dfrac{9}{8}kh^{2}}$

最後に,熱量は熱力学第一法則から求めましょう.
内部エネルギーの変化を$\Delta U$,気体が吸収する熱量を$Q$,気体がした仕事を$W$とすると
$Q=\Delta U+W$
★ 熱力学第一法則
$\eqalign{Q&=\varDelta U+W\\&=\dfrac{1}{2}p_{0}Sh+\dfrac{1}{2}mgh+\dfrac{1}{8}kh^{2}+\dfrac{3}{4}p_{0}Sh+\dfrac{3}{4}mgh+\dfrac{9}{8}kh^{2}\\&=\dfrac{5}{4}p_{0}Sh+\dfrac{5}{4}mgh+\dfrac{5}{4}kh^{2}}$ (答)


コメント