
今回は,斜面上の導体棒の運動です.
新しいことはありませんが,計算が複雑なのと,今までのことをしっかりと理解していないと,間違ってしまうので,必ず演習をしておくべき箇所です.
前回の問題はこちら
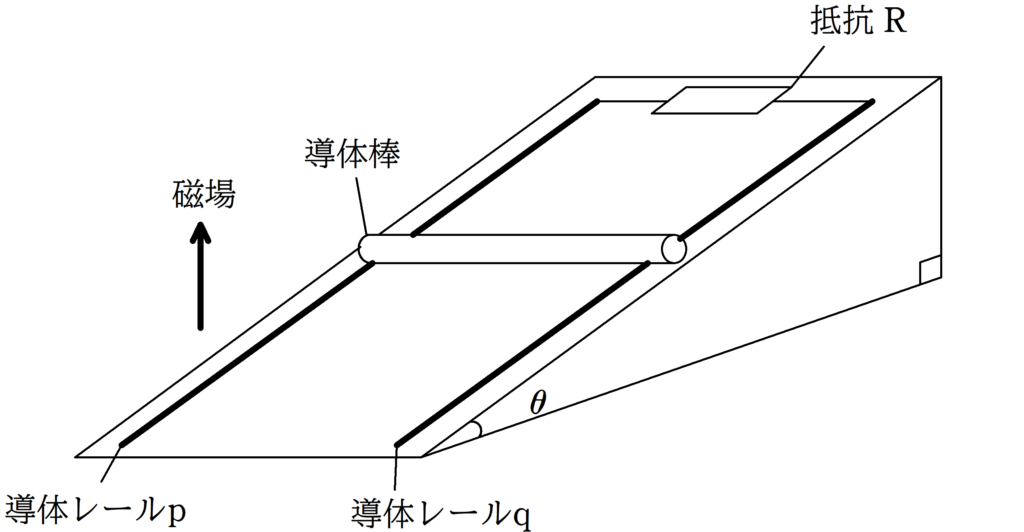
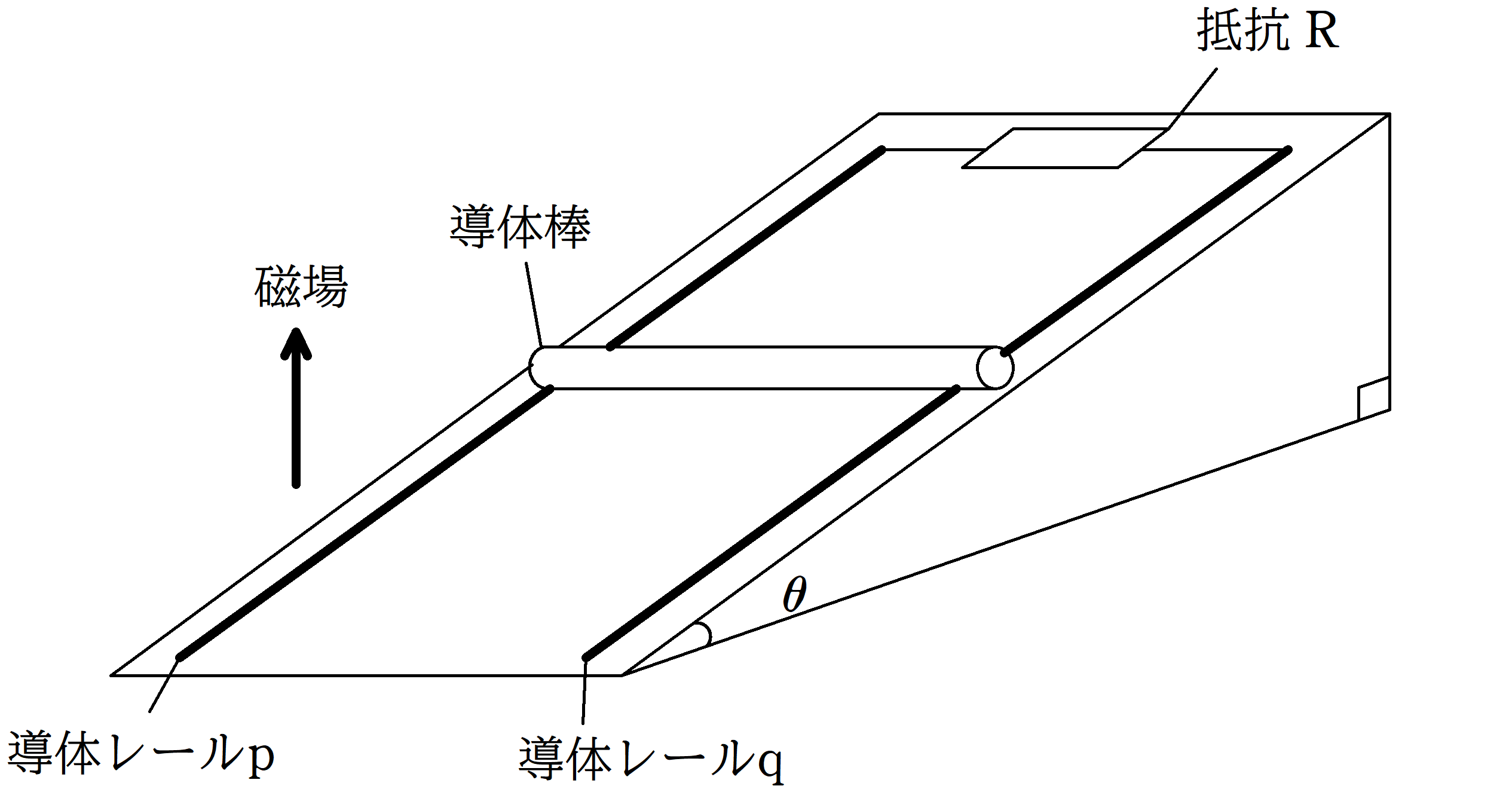
図のような,傾角$\theta$の斜面に導体レールp , qが距離$l$を隔てて,平行に敷かれている.
導体レールp , qは抵抗の無視できる導線によって,電気抵抗$R$の抵抗Rに接続されている.
鉛直上向きに磁束密度の大きさ$B$の一様な磁場がかかっている状態で,質量$m$の導体棒をレールに対して垂直におき,静かにはなした.
導体レールと導体棒の動摩擦係数を$\mu$,重力加速度の大きさを$g$として次の問いに答えよ.
(1) 導体棒をはなして,十分時間が経ったときの導体棒の速さを求めよ.
(2) 導体棒をはなして,十分時間が経ったときの電気抵抗Rで生じる消費電力を求めよ.
<解答>

毎回確認しているけど,基本は次の2つだよ.
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は,PQの長さを$l$,PQ方向に垂直な速さを$v_{\perp}$,導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば,
$V=v_{\perp}Bl$
- 回路の式(オームの法則,コンデンサーの基本式,電荷保存則など)
- 導体棒の運動に関する式(つり合いの式,運動方程式,運動量保存則など)
- 導体棒と回路の系全体のエネルギー収支の式

特に,この問題は磁場と導体棒の速度が垂直な関係になっていないので注意!
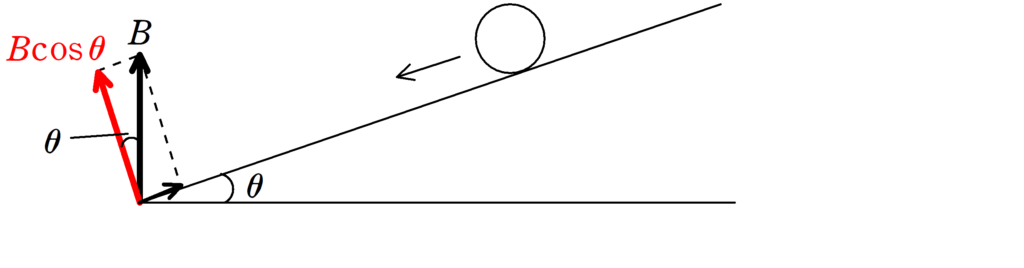

導体棒の速度に対して垂直な磁束密度の成分は$B\cos \theta$だね.
だから,導体棒に生じる誘導起電力の大きさ$V$は
$V=vB\cos\theta l$
だね.
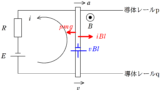
まずは,「1.回路の式」を立てるよ.
回路にあるのは,導体棒の誘導起電力と抵抗$R$だけ.
流れる電流を$i$と設定しましょう.
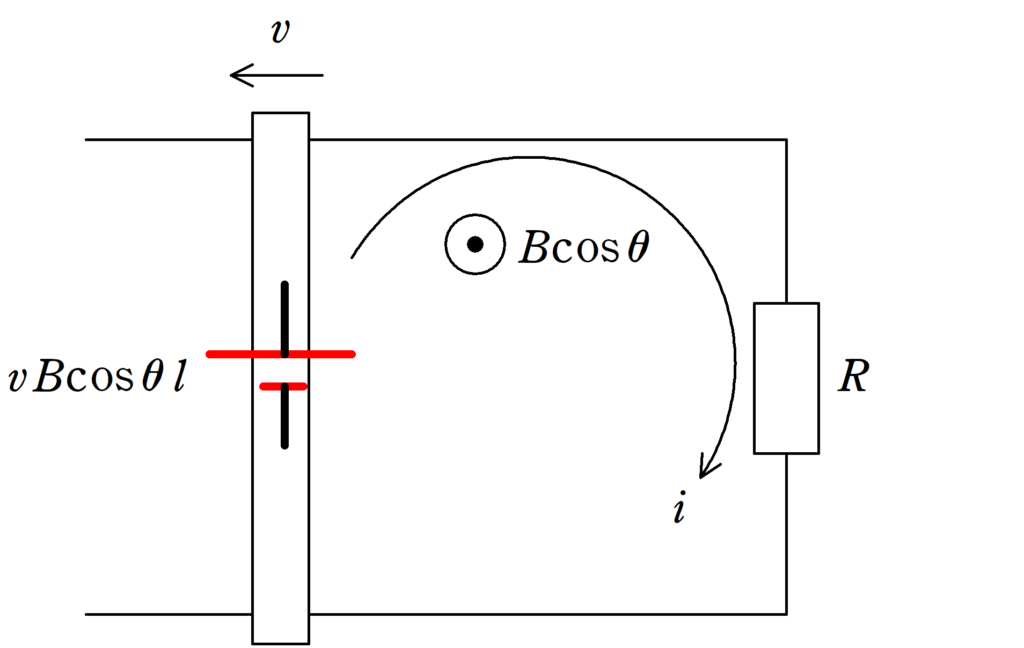

キルヒホッフの法則を立てれば次のようになるね.
$vBl\cos\theta=Ri$
$\therefore i=\dfrac{vBl\cos\theta}{R}$ $\dots (\ast)$

次に,「2.導体棒の運動方程式」を立てましょう.
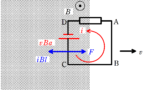
導体棒が速度$v$で,斜面下向きに加速度$a$であるときを考えましょう.
はたらく力は,重力,垂直抗力,電磁力,動摩擦力です.
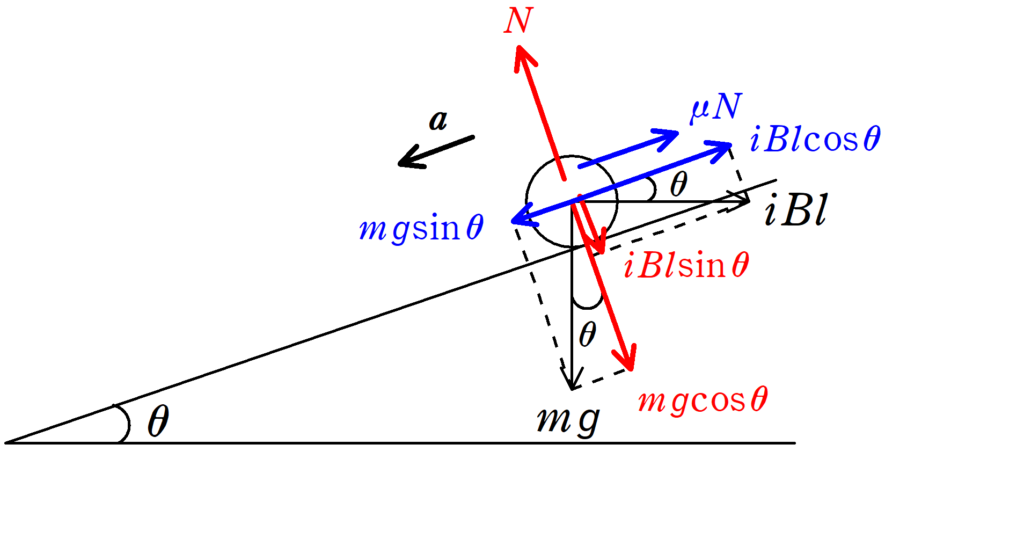

電磁力の間違いが多いので注意です.
誘導起電力が速度$v$に垂直な成分しかとらなかったので,電磁力も$B\cos\theta$のみを考える人が多いですが,電磁力は電流が磁場から受ける力です.
電流と磁束密度$B$は垂直な関係になっているので,そのままでOK.
フレミング左手の法則を使えば,上図の右方向に力がかかります.

斜面方向の運動方程式と,斜面に垂直な方向のつり合いの式を立てましょう.
垂直抗力は$N=mg\cos \theta$としないようにね!
★斜面垂直方向のつり合いの式
$N=mg\cos\theta +iBl\sin\theta$ $\dots (2\ast)$
★斜面方向の運動方程式
$ma=mg\sin\theta-\mu N-iBl\cos\theta$
$(2\ast)$の$N=mg\cos\theta +iBl\sin\theta$を代入して
$\eqalign{ma&=mg\sin\theta-\mu(mg\cos\theta +iBl\sin\theta)-iBl\cos\theta\\&=(\sin\theta-\mu\cos\theta)mg-iBl(\mu\sin\theta+\cos\theta)}$
$(\ast)$の$i=\dfrac{vBl\cos\theta}{R}$を代入して
$\eqalign{ma&=(\sin\theta-\mu\cos\theta)mg-\dfrac{vBl\cos\theta}{R}Bl(\mu \sin\theta+\cos\theta)\\&=-\dfrac{B^{2}l^{2}\cos\theta}{R}(\mu \sin\theta+\cos\theta)v+(\sin\theta-\mu\cos\theta)mg}$
もう一度書き直して
$ma=-\dfrac{B^{2}l^{2}\cos\theta}{R}(\mu \sin\theta+\cos\theta)v+(\sin\theta-\mu\cos\theta)mg$ $\dots (3\ast)$

かなり複雑な形に見えるけど,これは,運動方程式
$ma=-kv+C$
の形になっているよ.
この記事も参考にしてみてね.
質量を$m$,加速度を$a$,速度を$v$,$C$を定数とすると
$ma=-kv+C$
は終端速度型の運動方程式である.
終端速度型の運動方程式は次の特徴がある.
十分時間が経つと,速度が一定(加速度が0)になる.
速度が一定になったときの速度を終端速度という.
終端速度は運動方程式に$a=0$を代入して
$0=-kv+C$ $\therefore v=\dfrac{C}{k}$
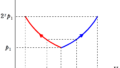
また,$t=0$のときの速度を$v_{0}$とすると,そのときの加速度($v-t$グラフの傾き)は
$a=\dfrac{-kv_{0}+C}{m}$
となる.

つまり,$(3\ast)$の運動方程式の形から
十分時間が経つと加速度$a$が0になることがわかるよ.
$(3\ast)$に$a=0$を代入して
$0=-\dfrac{B^{2}l^{2}\cos\theta}{R}(\mu \sin\theta+\cos\theta)v+(\sin\theta-\mu\cos\theta)mg$
$\therefore$ $v=\dfrac{\sin\theta-\mu\cos\theta}{\mu\sin\theta+\cos\theta}\cdot\dfrac{mgR}{B^{2}l^{2}\cos\theta}$
(2) このとき,$(\ast)$の$i=\dfrac{vBl\cos\theta}{R}$より
$i=\dfrac{\sin\theta-\mu\cos\theta}{\mu\sin\theta+\cos\theta}\cdot \dfrac{mg}{Bl}$
なので,抵抗Rで消費される電力$P$は
$\displaystyle{\eqalign{P&=i^{2}R\\&=\left\{\dfrac{\sin\theta-\mu\cos\theta}{\mu\sin\theta+\cos\theta}\cdot \dfrac{mg}{Bl}\right\}^{2}R}}$

電流を求めるには,導体棒の斜面方向のつり合いを考えてもいいよ.
また,消費電力は
重力の仕事率+摩擦力の仕事率
でも出せます!
次回の内容はこちらです.



コメント
[…] 斜面上の運動(摩擦あり) 導体棒の磁場中の運動演習⑧[基本]NEKO今回は,… 問題 […]
[…] 斜面上の運動(摩擦あり) 導体棒の磁場中の運動演習⑧[基本]NEKO今回は,… […]
[…] 斜面上の運動(摩擦あり) 導体棒の磁場中の運動演習⑧[基本]NEKO今回は,… […]