
基本問題も終盤です.
ここから2回かけて,コイルの問題を扱います.
コイルの問題も導体棒の問題と考えることができます.
前回の内容はこちら
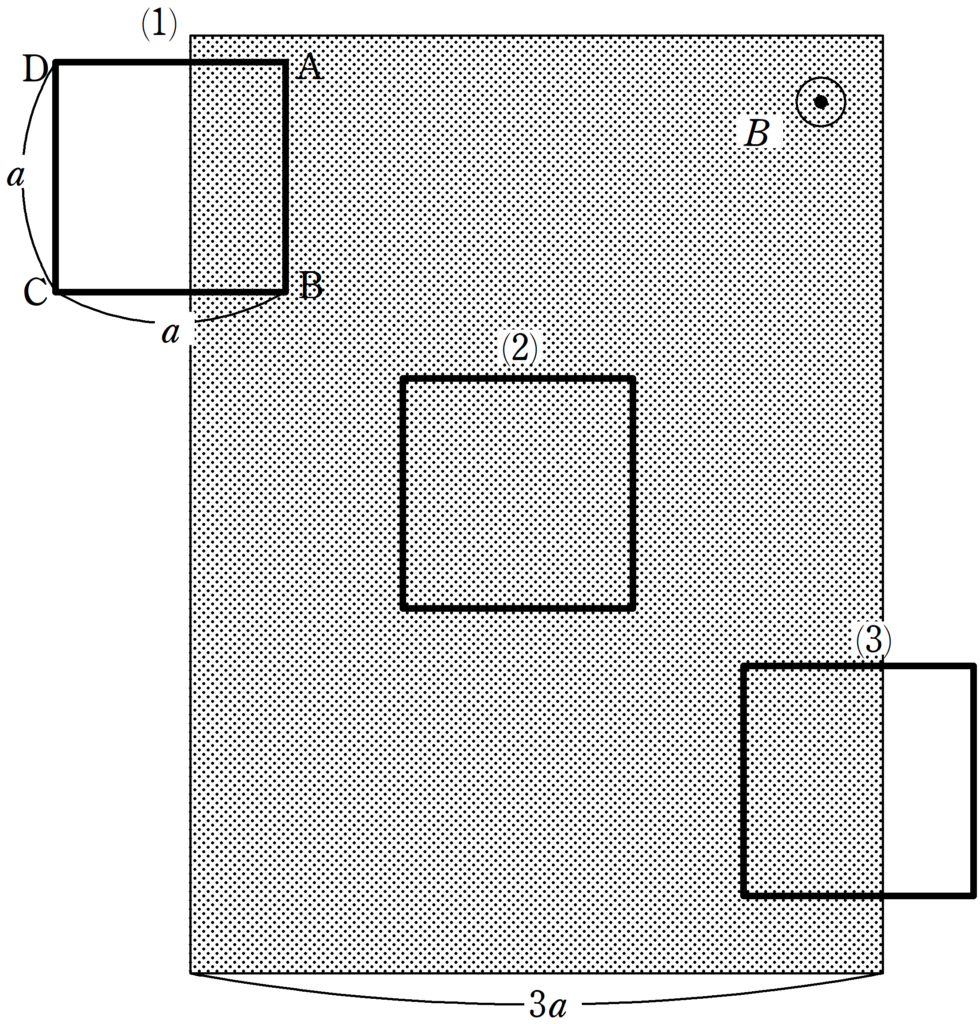
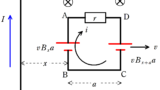
1辺の長さが$a$で全抵抗が$R$の正方形のコイルABCDがある.
この正方形コイルを一様な磁場がかけられている領域で速さ$v$の等速度運動させることを考える.
磁場の領域では,画面奥から手前方向に磁束密度$B$の磁場がかけられている.
上図の磁場の領域の左端の位置を原点として,右方向に$x$軸をとる.
正方形コイルABの座標を$x$として次の問いに答えよ.
ただし,コイルに流れる電流がつくる磁場の影響は無視をする.
(1) $0\leqq x\leqq a$ の間にコイルに加えている力を求めよ.また,この間の抵抗で発生するジュール熱を求めよ.
(2) $a\leqq x\leqq 3a$ の間にコイルに加えている力を求めよ.また,この間の抵抗で発生するジュール熱を求めよ.
(3) $3a\leqq x\leqq 4a$ の間にコイルに加えている力を求めよ.また,この間の抵抗で発生するジュール熱を求めよ.

では,解答です!
今回も次の2つの確認からです.
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は,PQの長さを$l$,PQ方向に垂直な速さを$v_{\perp}$,導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば,
$V=v_{\perp}Bl$
- 回路の式(オームの法則,コンデンサーの基本式,電荷保存則など)
- 導体棒の運動に関する式(つり合いの式,運動方程式,運動量保存則など)
- 導体棒と回路の系全体のエネルギー収支の式
(1)

まず,導体棒ABは速さ$v$で磁場中を動くので,起電力$vBa$の電池になるね.
CD部分はまだ磁場に入っていないので,誘導起電力は生じないよ.
また,AD部分やCB部分は一部磁場に入っているけど導線方向の速さをもっていないから,この方向に誘導起電力は生じないよ.

では,「1.回路の式」を立てましょう.
回路に流れる電流を$i$としましょう.
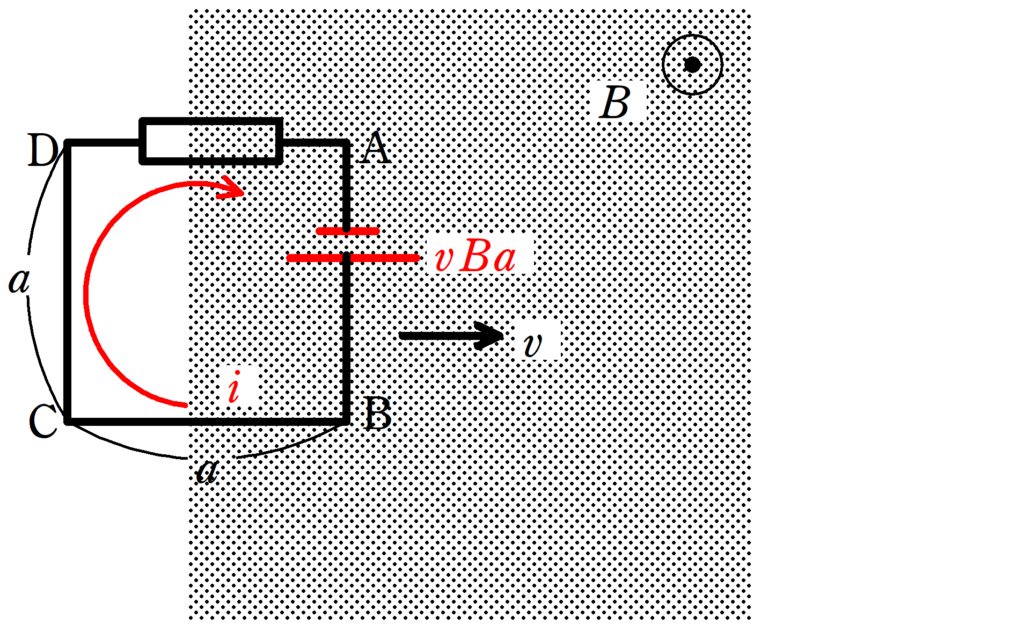
★キルヒホッフの法則より
$vBa=Ri$ $\therefore i=\dfrac{vBa}{R}$

磁場中に電流が流れると,電磁力を受けるね.
AB部分に流れる電流の電磁力について考えるんだけど,実はADとBCの磁場に入っている場所にも電磁力がはたらいているよ.
ただ,電磁力の大きさが同じで向きが反対なので,つり合っているんです.
また,CD部分に関しては磁場に入っていないので,電磁力はたらかないよ.
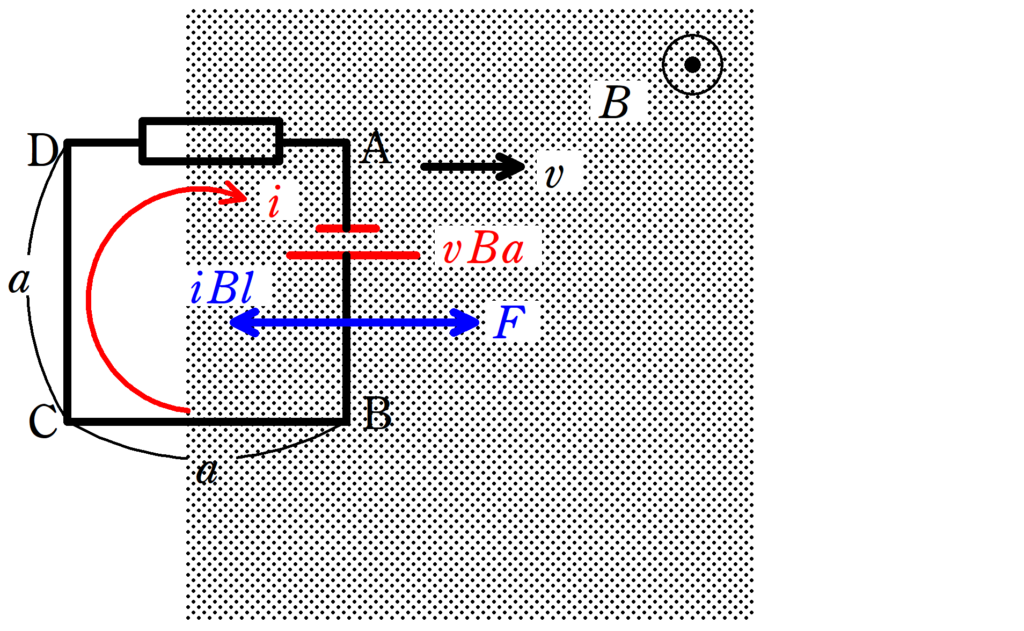

AB部分にはたらく電磁力は,フレミング左手の法則を考えれば
左向きに$iBa=\dfrac{vB^{2}a^{2}}{R}$
になるね.
上の式では,キルヒホッフの法則から導出した$i=\dfrac{vBa}{R}$を代入したよ.

コイルは等速度運動
→コイルの加速度0
→コイルにはたらく力はつりあっている
ので,外から加える力は電磁力と同じ大きさで向きは反対だね.
つまり,加える外力の大きさは$\dfrac{vB^{2}a^{2}}{R}$で向きは右向き.

次に抵抗で発生するジュール熱の計算です.
今回は次の2通りの方法で求めることができます.
- エネルギー収支の式を立てる.
- $Q=i^{2}Rt$の式から求める.
2つの方法で解いてみましょう.
1. エネルギー収支の式
エネルギー収支の式を立てると
外力がした仕事=ジュール熱
です.
なぜ,電磁力がした仕事を含めないのかが気になる人はこちらを参照してください
$0\leqq x\leqq a$までに外力がした仕事$W$は
$W=Fa=\dfrac{vB^{2}a^{3}}{R}$
です.したがって,ジュール熱も$\dfrac{vB^{2}a^{3}}{R}$
2. $Q=i^{2}Rt$の式
$0\leqq x \leqq a$移動するのにかかった時間は$\dfrac{a}{v}$なので,求めるジュール熱は
$\eqalign{Q&=i^{2}Rt\\&=(\dfrac{vBa}{R})^{2}\cdot R\cdot \dfrac{a}{v}\\&=\dfrac{vB^{2}a^{3}}{R}}$
したがって,こちらもジュール熱は$\dfrac{vB^{2}a^{3}}{R}$です.
(2)
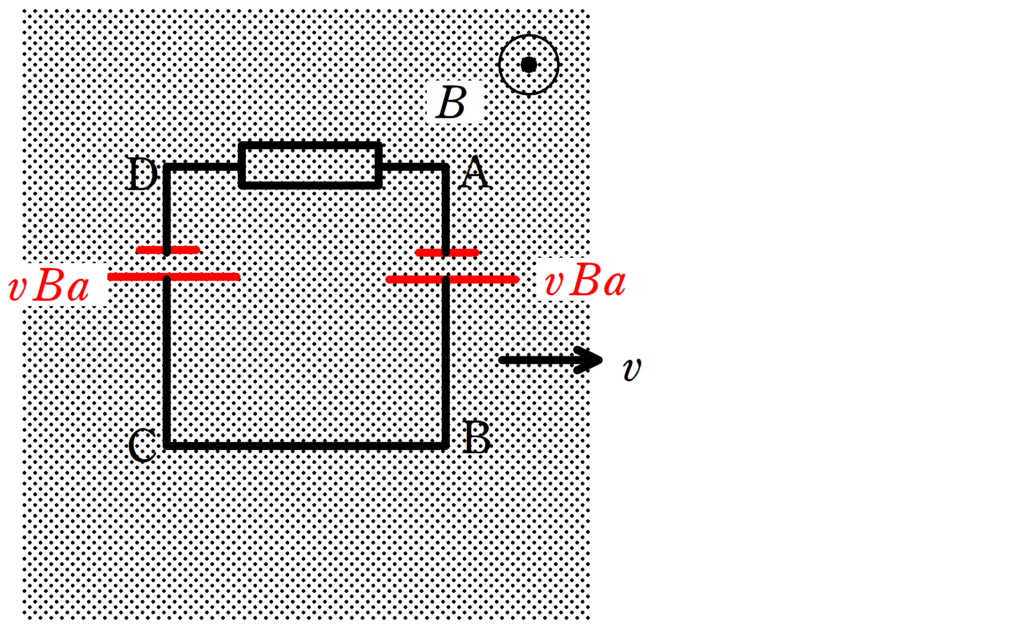

次に,$a\leqq x\leqq 3a$では,導体棒ABとCDはどちらも大きさが$vBa$で向きが逆の誘導起電力が生じるので,電流は流れません.
つまり,導体棒に電磁力がはたらかないので,外力が加える力も0です.
もちろん,ジュール熱も0です.
(3)
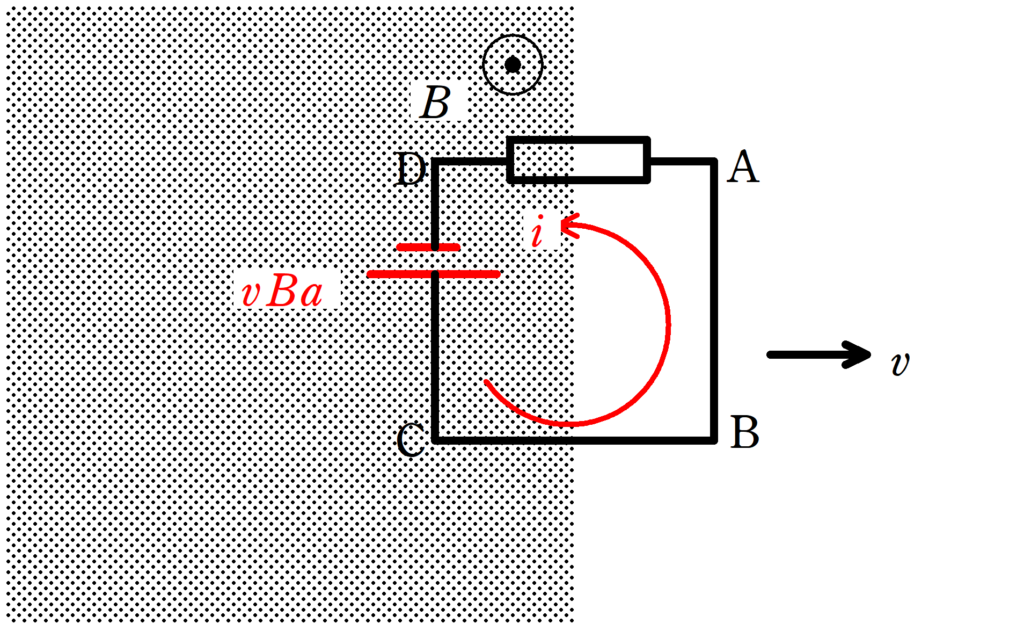

$3a\leqq x\leqq 4a$では,導体棒CDだけ誘導起電力が生じます.
流れる電流を$i$として,キルヒホッフの法則を立てましょう.
★キルヒホッフの法則より
$vBa=Ri$ $\therefore i=\dfrac{vBa}{R}$

すると(1)と同様に電磁力が生じます.
計算自体は(1)と変わりませんね.
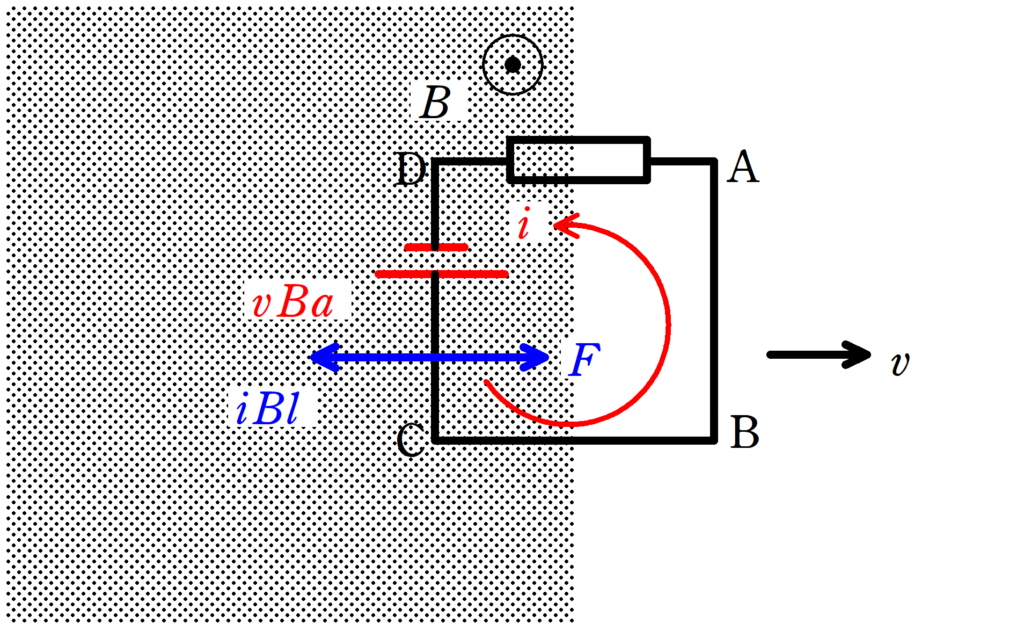
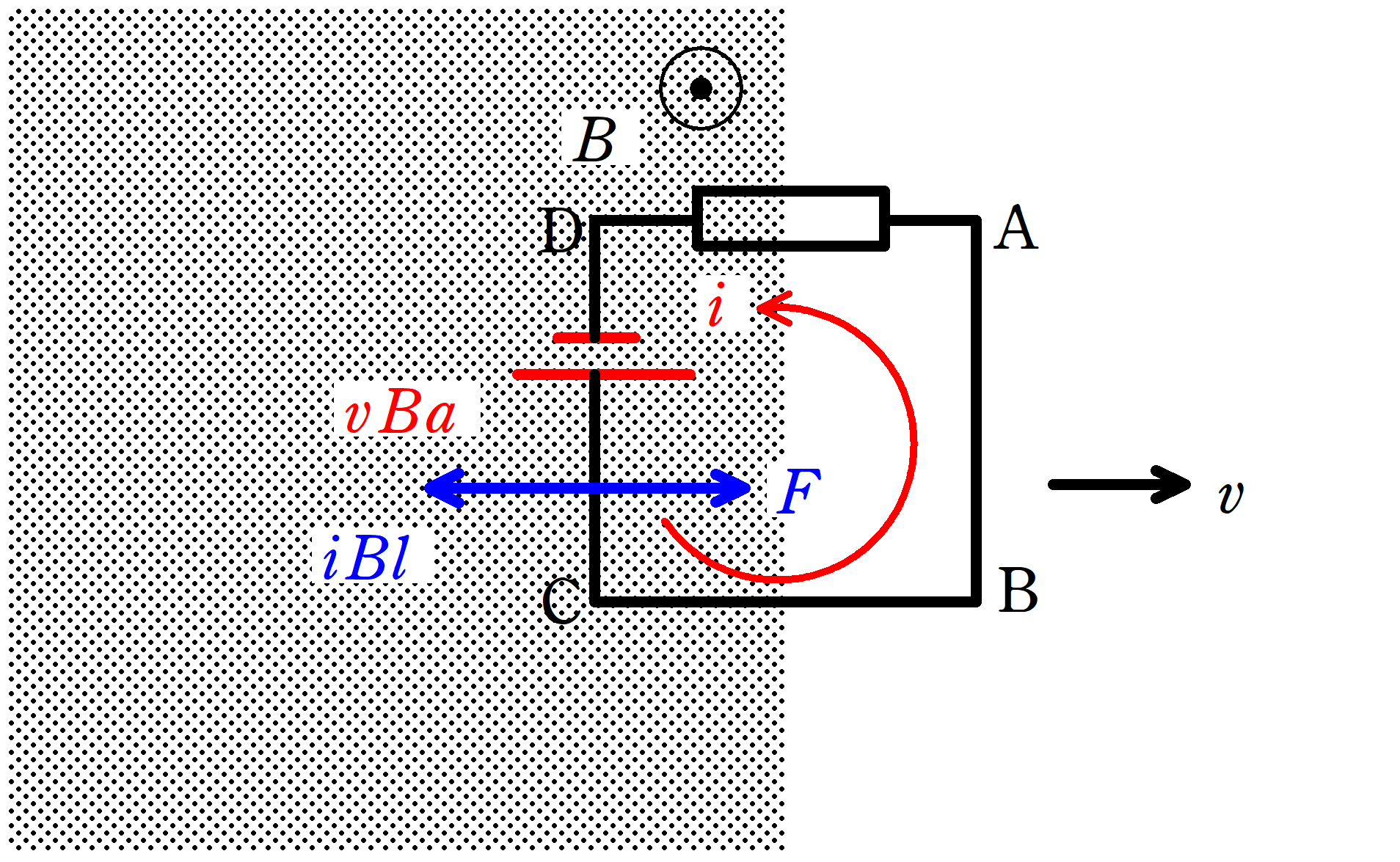
加える外力の大きさは$F=iBl=\dfrac{vB^{2}a^{2}}{R}$(右向き),生じるジュール熱は$\dfrac{vB^{2}a^{3}}{R}$です.

次回の内容はこちらです.


コメント
[…] […]