
前回の内容はこちらです.(1)(2)は前回の内容と同じです.
一見,似たような問題ですが,スイッチの操作に若干に違いがあります.
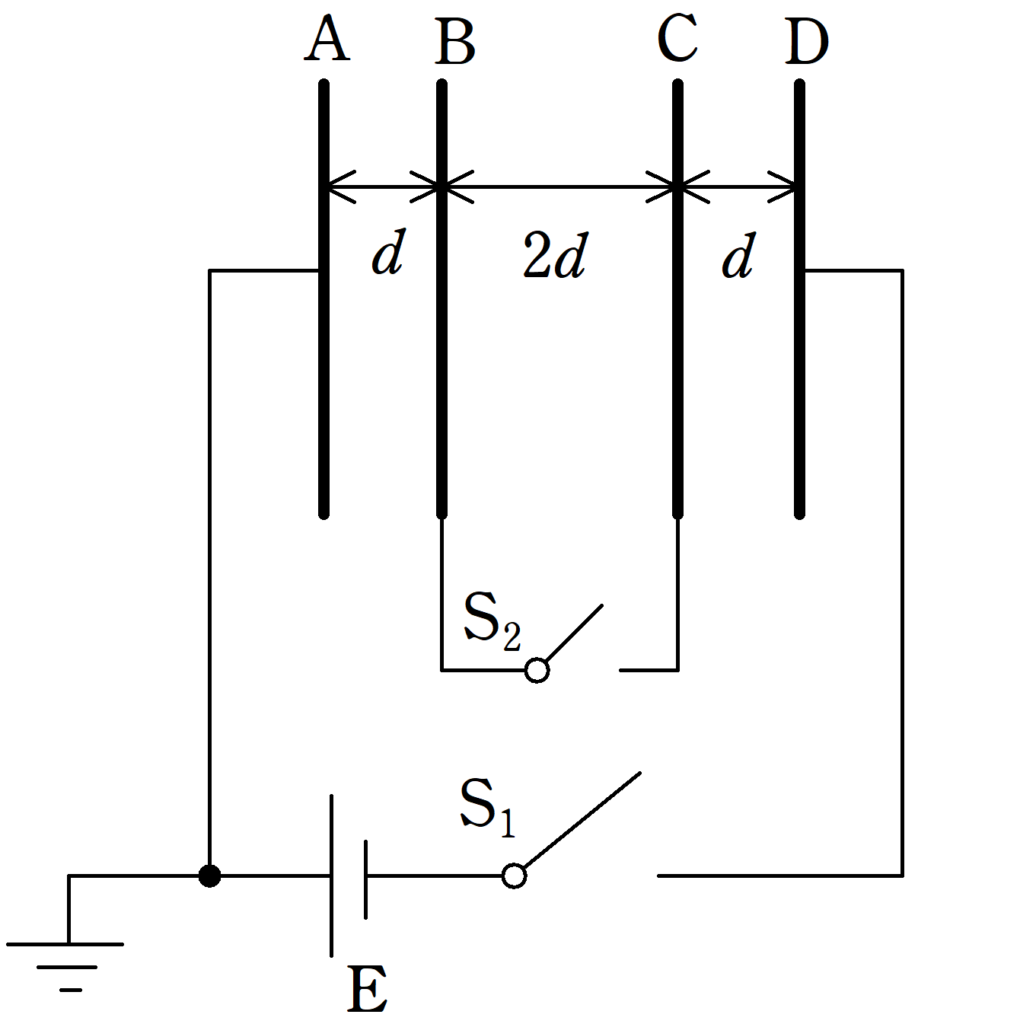
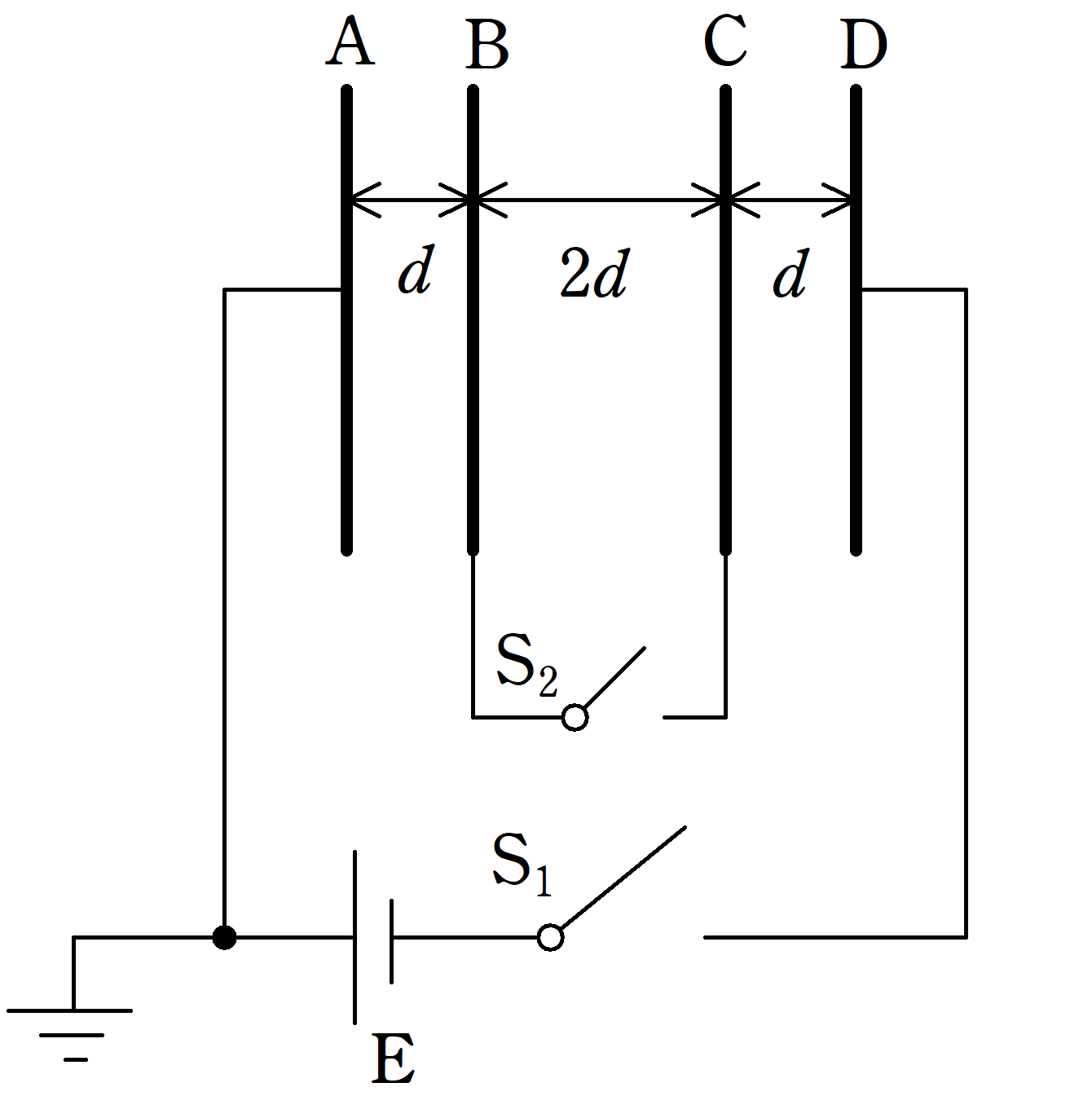
図のように面積$S$の4枚の薄い金属板A,B,C,Dが平行に並べてあり,スイッチ$\rm S_{1}$,$\rm S_{2}$と,起電力$V$の電池E,アースが接続されている.AB,BC,CDの距離は$d$,$2d$,$d$であり,$d$は金属板の面積$S$に対して十分小さい.
はじめ,スイッチ$\rm S_{1}$,$\rm S_{2}$は開いており,すべての極板には電荷が蓄えられていなかった.以下,真空の誘電率を$\varepsilon_{0}$とする.
まず,スイッチ$\rm S_{1}$を閉じて十分時間が経過したところ,極板Aには電荷$Q(>0)$が蓄えられた.
(1) AB間,BC間,CD間の電場の大きさ$E_{\rm AB}$,$E_{\rm BC}$,$E_{\rm CD}$を$Q$,$\varepsilon_{0}$,$S$を用いて表せ.
(2) AD間の電位差が$V$であることを用いて,電荷$Q$を$\varepsilon_{0}$,$S$,$d$,$V$を用いて表せ.
次にスイッチ$\rm S_{1}$を閉じたままにスイッチ$\rm S_{2}$を閉じて十分時間が経過した.
(3) 極板Aに蓄えられている電荷を$Q^{\prime}$,Dに蓄えられる電荷を$-Q^{\prime}$が蓄えられたとする.このとき,AB間,BC間,CD間の電場の大きさ$E_{\rm AB}^{\prime}$,$E_{\rm BC}^{\prime}$,$E_{\rm CD}^{\prime}$を$Q^{\prime}$,$\varepsilon_{0}$,$S$を用いて表せ.
(4) AD間の電位差が$V$であることを用いて,$Q^{\prime}$を$\varepsilon_{0}$,$S$,$d$,$V$を用いて表せ.
<解答>

平面に分布している電荷がつくる電場は次のようになります.
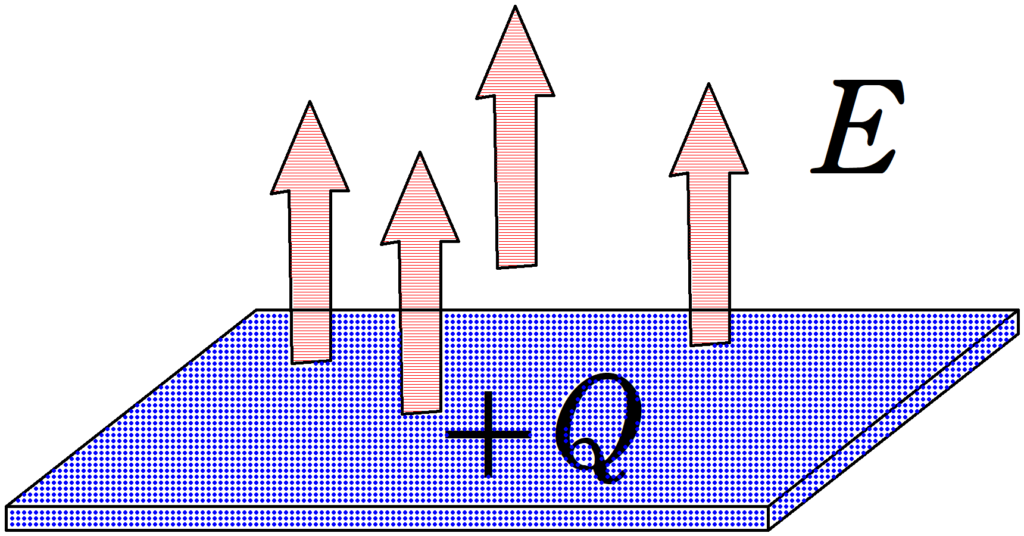
十分に広い平面に一様な電荷$Q$が分布している.
真空の誘電率を$\varepsilon_{0}$,平面の面積を$S$とするとき,電場の大きさ$E$は
$E=\dfrac{|Q|}{2\varepsilon_{0}S}$
これは,電場が距離によらず一定であることを意味している.
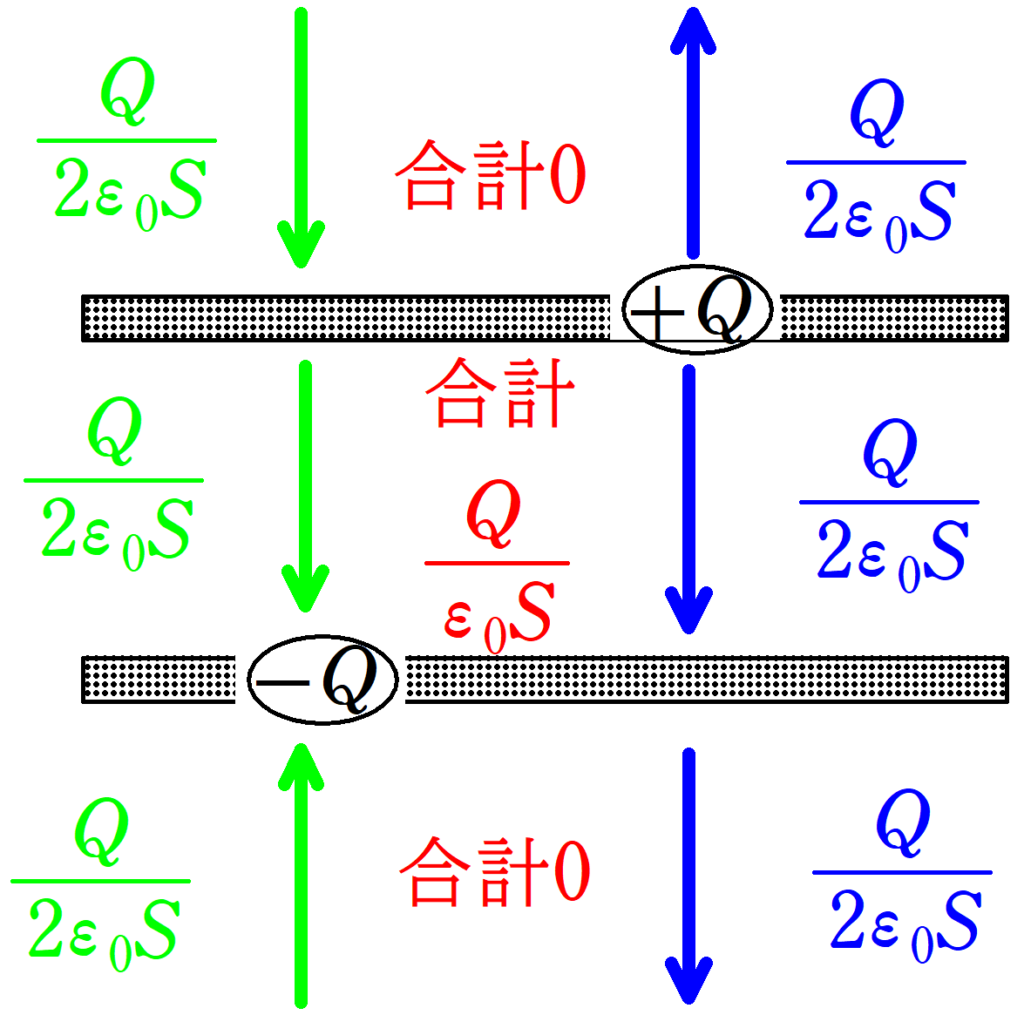

さらに,$+Q$,$-Q$の蓄えられた電荷がつくる電場によって,その内部の電場は$\dfrac{Q}{\varepsilon_{0}S}$になり,外部の電場は0になります.
Aに電荷$Q$が蓄えられると,Bの左部分に$-Q$が蓄えられ,Bの電荷はもともと0だったので,電荷保存則より,Bの右側部分の電荷は$Q$になります.
すると,Cの左部分は電荷が$-Q$になり,Cの電荷保存則より,Cの右側部分の電荷が$Q$になり,その結果Dの電荷は$-Q$となります.
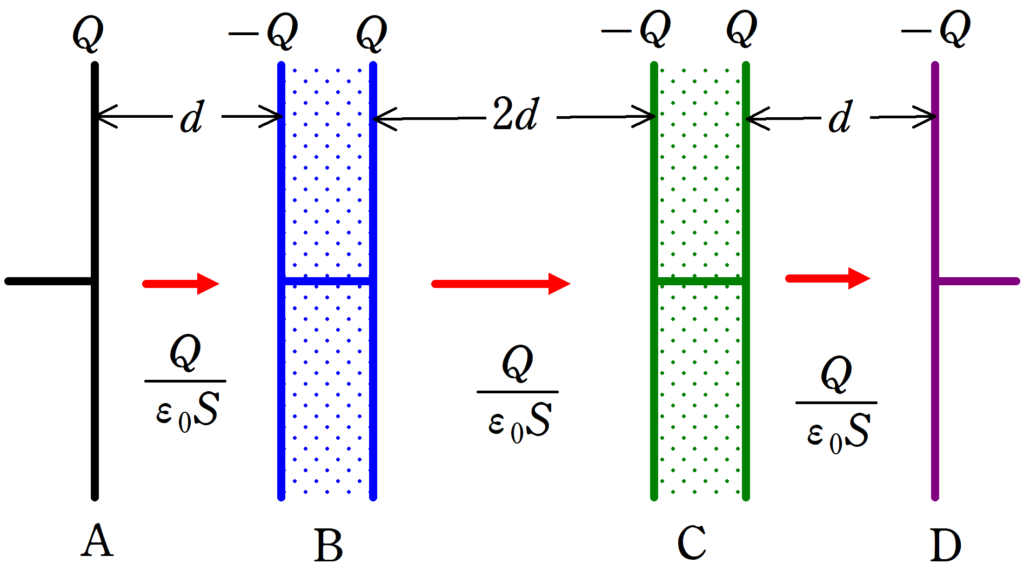
したがって,
$E_{\rm AB}=E_{\rm BC}=E_{\rm CD}=\dfrac{Q}{\varepsilon_{0}S}$(答)
(2)

電場の大きさと電位差の関係は次のようになります.
電場の大きさを$E$,距離$\Delta x$の電位差を$\Delta V$とするとき,次の関係が成り立つ.
$E=\left|\dfrac{\Delta V}{\Delta x}\right|$
★ キルヒホッフ(電圧降下の式)則
AB間,BC間,CD間の電位差の和が$V$なので,
$\dfrac{Q}{\varepsilon_{0}S}\cdot d+\dfrac{Q}{\varepsilon_{0}S}\cdot 2d+\dfrac{Q}{\varepsilon_{0}S}\cdot d=V$
$\therefore Q=\dfrac{\varepsilon_{0}S}{4d}V$ (答)
(3)
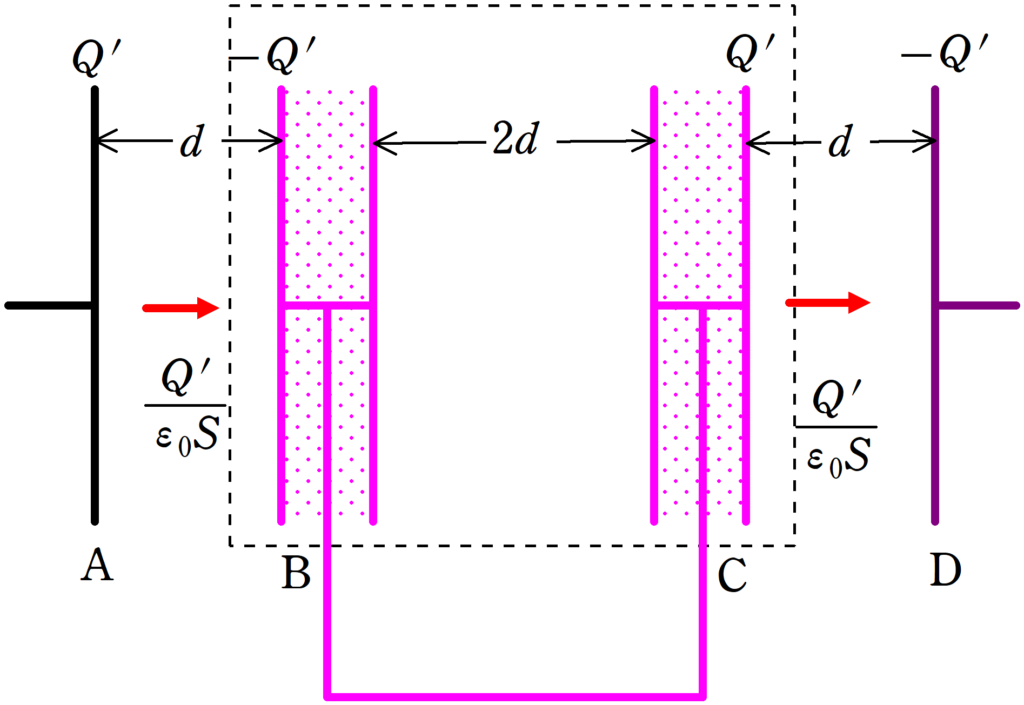

Aに蓄えられている電荷が$Q^{\prime}$であるとき,Bの左部分に電荷$-Q^{\prime}$が帯電します.
BとCの間に電位差がないので,Bの右側とCの左側には電荷は蓄えられていません.
電荷保存則より,Cの右側には電荷$Q^{\prime}$が蓄えられ,Dには電荷$-Q^{\prime}$が蓄えられます.
したがって,
$E_{\rm AB}^{\prime}=E_{\rm CD}^{\prime}=\dfrac{Q^{\prime}}{\varepsilon_{0}S}$(答)
$E_{\rm BC}^{\prime}=0$(答)
(4)

起電力$V$の電池につないだままなので,AD間の電位差は$V$です.
★ キルヒホッフ(電圧降下の式)則
$V=\dfrac{Q^{\prime}}{\varepsilon_{0}S}\cdot d+\dfrac{Q^{\prime}}{\varepsilon_{0}S}\cdot d$
$Q^{\prime}=\dfrac{\varepsilon_{0}S}{2d}V$ (答)

コメント