[演習]万有引力の問題１

問題

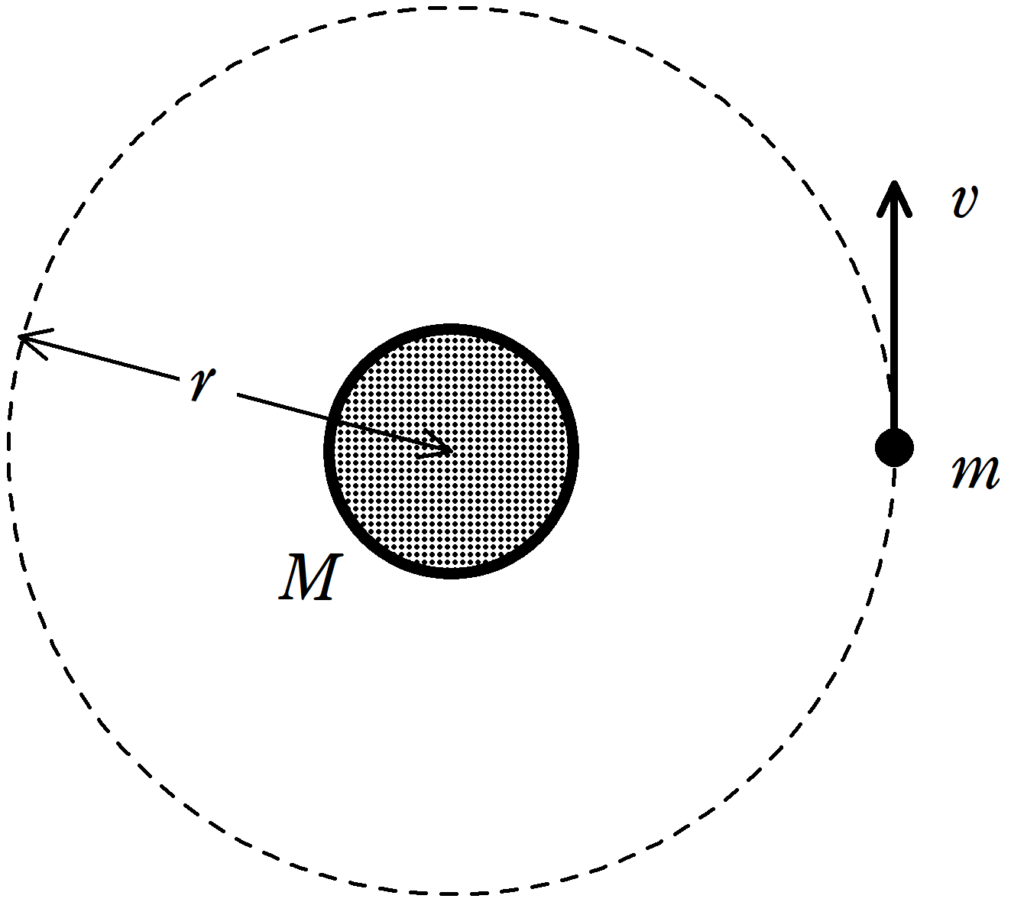
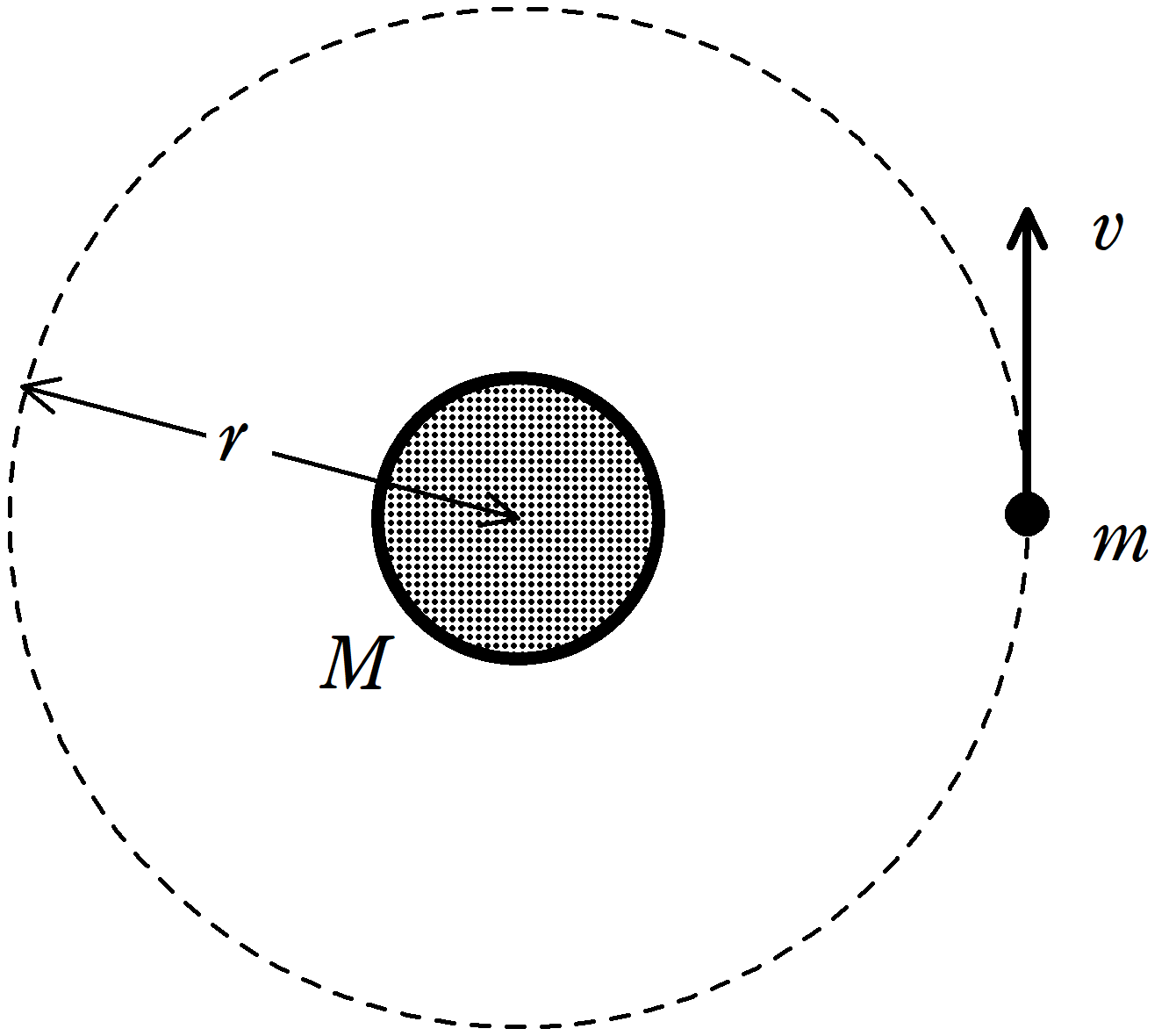
図のように，質量$M$の惑星Aとそのまわりをまわっている質量$m$の人工衛星について考える．人工衛星は半径$r$，速さ$v$の等速円運動をしている．惑星Aの質量は人工衛星の質量に比べて十分大きく，静止しているものとして考えることができる．万有引力定数を$G$として，惑星Aの自転は考えないものとする．

(1)　$v$を$G$，$r$，$M$を用いて表せ．

(2)　人工衛星の円運動の周期$T$とする．$\dfrac{T^{2}}{r^{3}}$を$G$，$M$を用いて表せ．

(3)　惑星Aと人工衛星の間の万有引力の位置エネルギー$U$を$G$，$r$，$M$，$m$を用いて表せ．ただし，万有引力による位置ネルギーの基準点は無限遠とする．

＜解答＞

PHYさん

万有引力の大きさについて確認しておきましょう．

万有引力

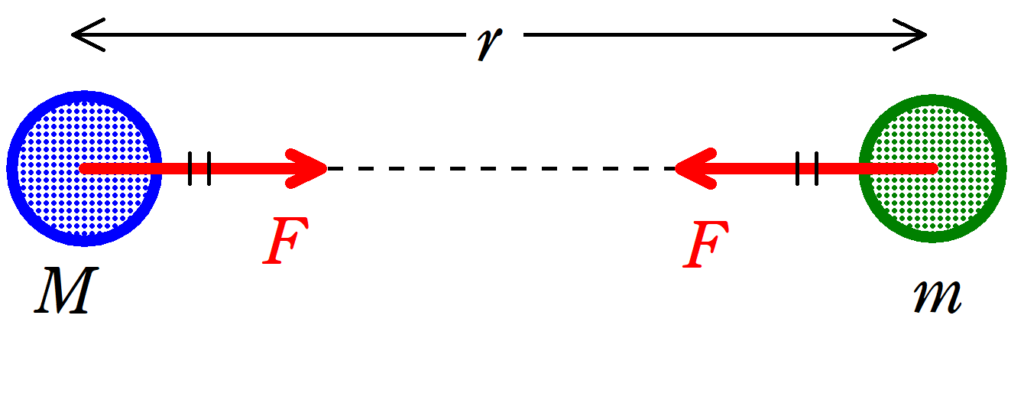
質量$M$の物体と質量$m$の物体の重心間の距離を$r$とする．万有引力定数を$G$とするとき，万有引力の大きさ$F$は

$F=G\dfrac{Mm}{r^{2}}$

NEKO

等速円運動の問題なので，次の2式を立てることを意識しましょう．

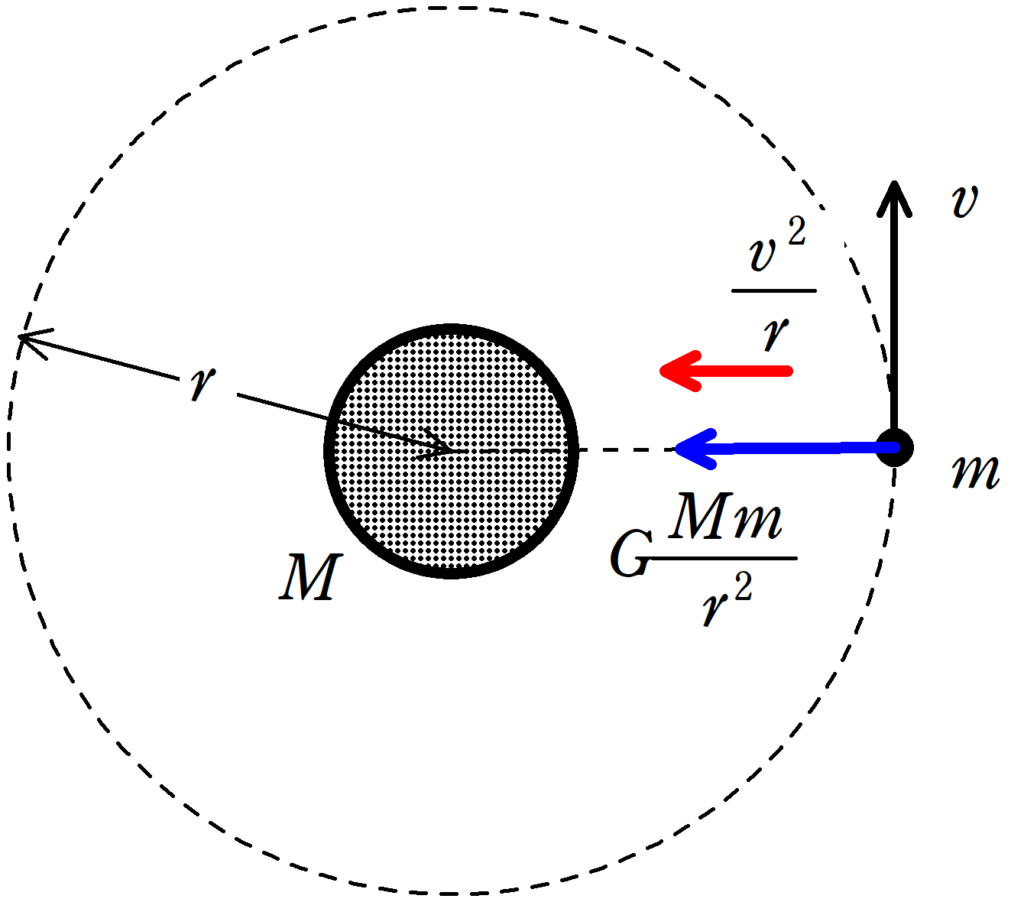
★　向心方向の運動方程式

$m\dfrac{v^{2}}{r}=G\dfrac{Mm}{r^{2}}$

$\therefore　v=\sqrt{\dfrac{GM}{r}}$（答）　$\dots　(\ast)$

(2)　

★　円運動の周期の式

$T=\dfrac{2\pi r}{v}$　$\dots　(2\ast)$

NEKO

$(\ast)$，$(2\ast)$より，$v$を消去します．

$(\ast)$を$(2\ast)$に代入して

$T=2\pi r\sqrt{\dfrac{r}{GM}}$

両辺2乗して

$T^{2}=4\pi^{2}r^{2}\cdot \dfrac{r}{GM}$

$\therefore　\dfrac{T^{2}}{r^{3}}=\dfrac{4\pi^{2}}{GM}$　(答)

PHYさん

この結果は，ケプラーの第2法則

「周期の2乗は長半径の3乗に比例する」

の円運動バージョンです．

(3)

万有引力による位置エネルギー

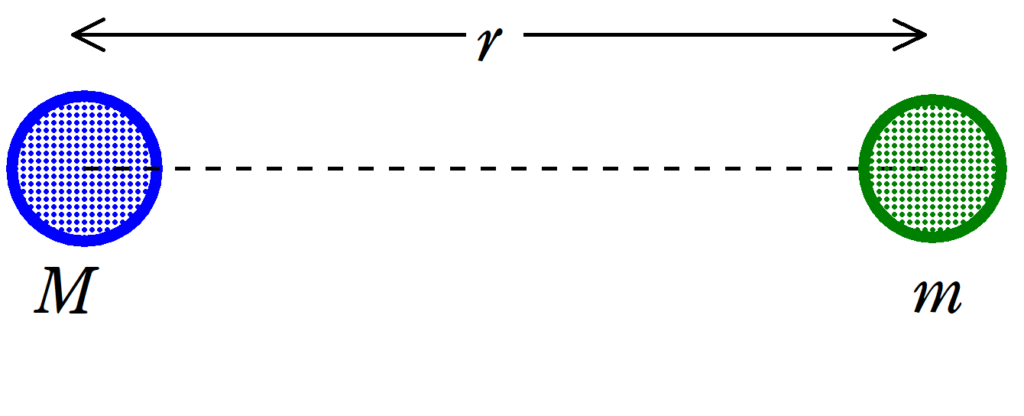
質量$M$と質量$m$の物体の距離を$r$とする．万有引力の位置エネルギーの基準点を無限遠とし，万有引力定数を$G$とすると，万有引力のよる位置エネルギー$U$は

$U=-G\dfrac{Mm}{r}$

★　万有引力のよる位置エネルギー$U$

$U=-G\dfrac{Mm}{r}$　(答)

PHYさん

次回の内容はこちらです．

[演習]万有引力の問題2　宇宙速度

問題上図のように質量$M$で半径$R$の惑星Aがある．惑星Aの自転の影響は無視をする．惑星Ａの表面上に質量$m$の物体があり，この物体に与える初速度によって，物体は様々な軌道を描く．万有引力定数を$G$として次の問いに答えよ．ただし，空気抵...

physicmath.net

2021.04.09