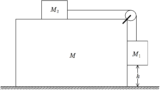
図に示すように質量$M$の直方体が水平面上に置かれている．$M$の上に置かれた質量$M_{2}$の物体から水平面に張ったひもを滑車にかけ，その先端に質量$M_{1}$の物体を鉛直につり下げる．$M_{1}$の側面は$M$と接し，上下になめらかなにすべることができるが，離れないような構造になっている．ただし，ひもは伸びず，その質量は無視できる．また，重力加速度は$g$である．
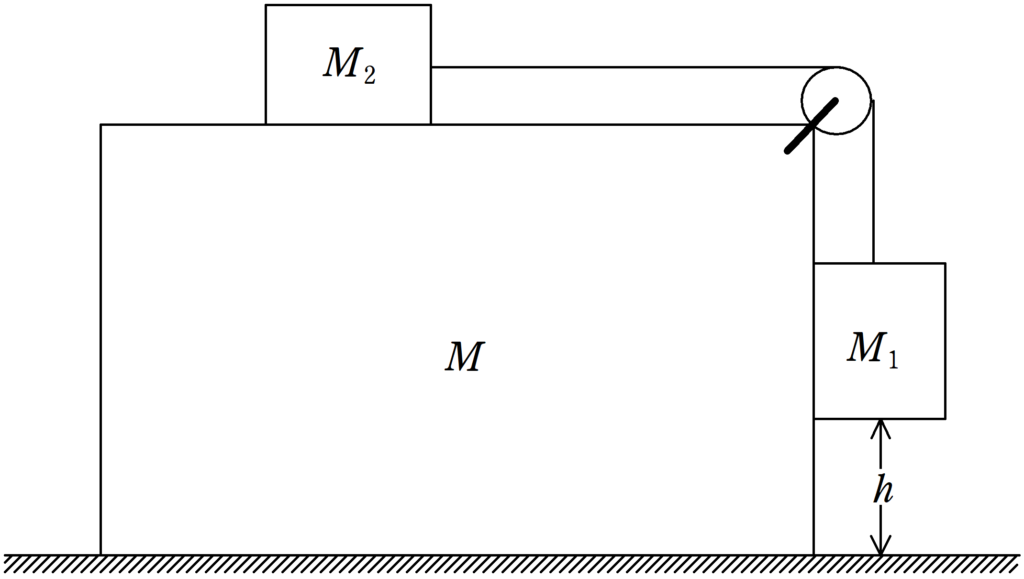
問 $M_{2}$と$M$の間および$M$と水平面の間に摩擦がないものとし，$M_{1}$の底面の高さが$h$になるように$M_{2}$と$M$をおさえた状態から手をはなした．$M_{1}$が水平面に達するまでの間に$M$が動く距離$x$を求めよ．
＜解法2＞
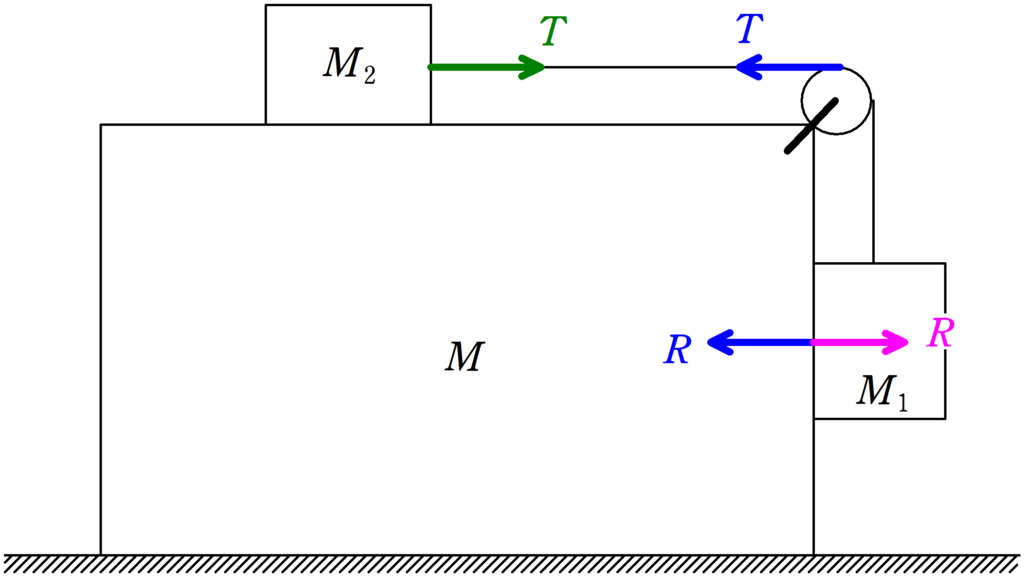
質量$M$，$M_{1}$，$M_{2}$の物体にはたらく水平方向の力をかくと，上図のようになります．
すると，力の和は0であることがわかります．
力の和が0のとき，運動量が保存します．
質量$M$の物体と質量$M_{1}$の物体は密着しているので，水平方向の速度は同じです．
運動を開始した時刻を$t=0$とし，時刻$t$における質量$M$と$M_{1}$の速度を$V$，質量$M_{2}$の物体を$V_{2}$とします．
すると，運動量保存則より
$0=(M+M_{1})V+M_{2}V_{2}$
となります．
両辺$\varDelta t$をかけて
$0=(M+M_{1})V\varDelta t+M_{2}V_{2}\varDelta t$
$\varDelta X=V\varDelta t$，$\varDelta X_{2}=V_{2}\varDelta t$とおくと，
$0=(M+M_{1})\varDelta X+M_{2}\varDelta X_{2}$ $\dots (\ast)$
になります．
$\varDelta X$は質量$M$と$M_{1}$の物体の水平方向の位置の変化（右方向を正とする），$\varDelta X_{2}$は質量$M_{2}$の物体の位置の変化です．
注意して欲しいのが，$V$と$V_{2}$が水平面で静止している人からみた速度なので，$\varDelta X$，$\varDelta X_{2}$も水平面で静止している人からみた位置の変化です．
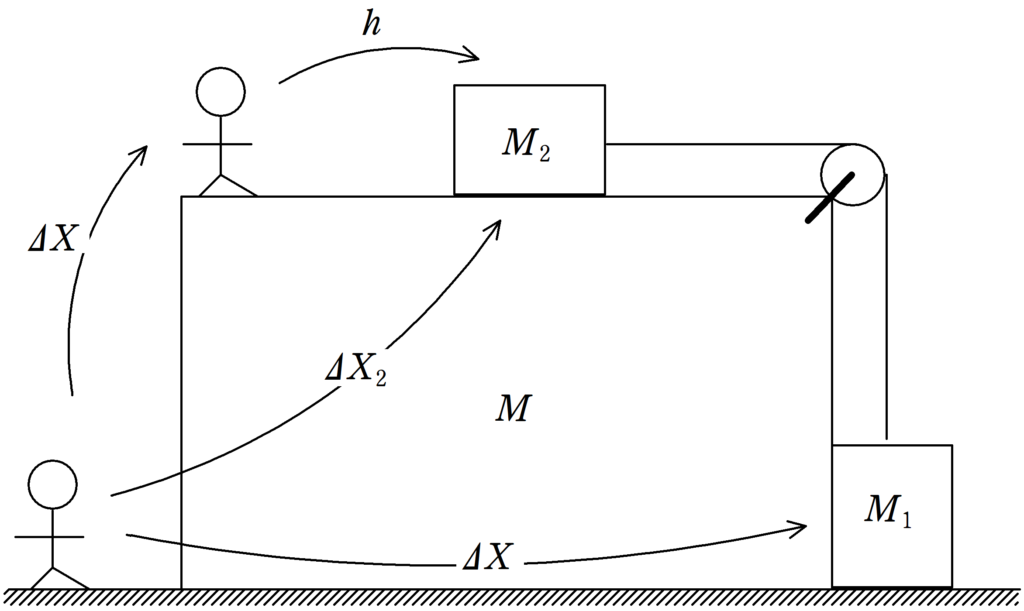
上図から，$\varDelta X$と$h$と$\varDelta X_{2}$には次の関係があります．
$\varDelta X_{2}=\varDelta X+h$ $\dots (2\ast)$
$(2\ast)$を$(\ast)$に代入すると
$\eqalign{(M+M_{1})\varDelta X+M_{2}(\varDelta X+h)&=0\cr (M_{1}+M_{2}+M)\varDelta X&=-M_{2}h\cr \varDelta X&=-\dfrac{M_{2}}{M_{1}+M_{2}+M}h}$
したがって，答えは$x=|\varDelta X|=\dfrac{M_{2}}{M_{1}+M_{2}+M}h$となります．
こちらの方が簡単ですね！
コメント