
今回の記事は次の方におすすめです.
- 静電気力と外力の正負について混乱している.
- そもそも問題のイメージがわかない.
- 仕事の正負について,確実に〇をもらいたい.

まずはポイントをまとめておきましょう.
静電気力がする仕事を$W_{静電気力}$,外力がする仕事を$W_{外力}$,位置エネルギーの変化を$\Delta U$とする.
★外力を加えて荷電粒子をゆっくりと動かす場合
$\Delta U=W_{外力}$,$W_{静電気力}+W_{外力}=0$ $\dots (\ast)$
★荷電粒子が静電気力を受けて自由に動く場合
$W_{静電気力}=-\Delta U$ $\dots (2\ast)$

$(\ast)$はエネルギーの原理の式だね!
運動エネルギーの変化=外力がした仕事
の外力がした仕事を保存力がした仕事と非保存力がした仕事に分けて書くと
運動エネルギーの変化=保存力がした仕事+非保存力がした仕事
となるね.
ここで,「ゆっくり」という表現は「運動エネルギーを変化させない」と読み取ります.
保存力がした仕事を$W_{保存力}$,外力がした仕事(非保存力がした仕事)を$W_{外力}$とすれば,
$0=W_{保存力}+W_{外力}$
を得ることができるよ.

また,保存力が正の仕事をした分だけ位置エネルギーは下がってしまい,保存力が負の仕事をすると,位置エネルギーは上昇するんだったね.
たとえば,重力が正の仕事をすると,正の仕事をしてしまった分,潜在的なエネルギー(位置エネルギー)は失ってしまったんだよ.もう仕事しちゃったからね.
このように,位置エネルギーの変化$\Delta U$と保存力がした仕事$W_{保存力}$は次のような関係があるよ.
$\Delta U=-W_{保存力}$
これは,知らない人が多いけど,結構大事な式なんだ!
しっかりと理解しておこう!

また,今回は静電気力の話なので,静電気力の位置エネルギーに関する知識もまとめておきましょう.
電気量$q$の電荷が電位$V$の位置にあるときの位置エネルギー$U$は
$U=qV$

重力による位置エネルギーだったら,
質量$m$の物体が重力加速度の大きさ$g$の中で,基準点からの高さ$h$上にあるときの位置エネルギー$U$は
$U=mgh$
だったね.重力の場合は物質固有の物理量である質量と高さによって位置エネルギーが決まるんだね.
一方,静電気力による位置エネルギーは,物質固有の物理量である電荷と電位の高さによって決まるんだね.

では,さっそく問題を解いてみましょう.
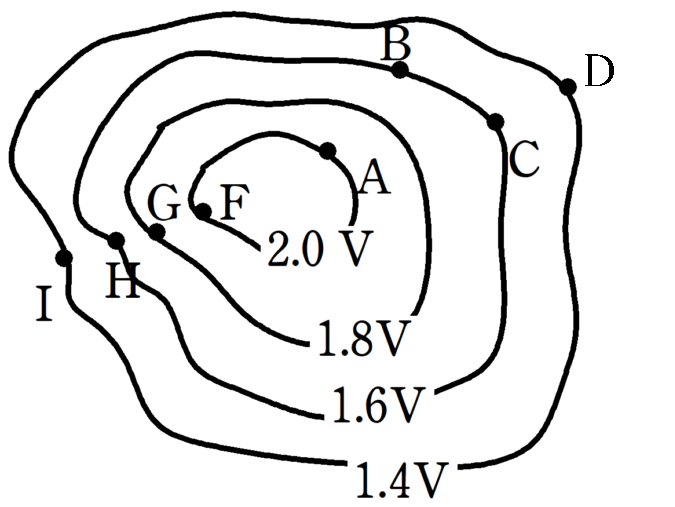
上図のような等電位面がある.このとき,次の問いに答えよ.
(1) $3.0 \rm C$の荷電粒子をA→B→C→Dへゆっくりと動かしたときの外力がした仕事と静電気力がした仕事をそれぞれ求めよ.
(2) $-2.0 \rm C$の荷電粒子をIに静かにはなすと,I→H→G→Fと移動した.このとき静電気力がする仕事を求めよ.
(1)

静電気力は保存力なので,経路にはよらず,最初と最後に位置によって仕事が決まります.
まず,A→Eに関して,位置エネルギーの変化$\Delta U_{\rm AD}$は
$\Delta U_{\rm AE}=3.0×(1.4-2.0)=-1.8 {\rm J}$
静電気力がする仕事(これが保存力がする仕事)を$W_{静電気力}$,外力がする仕事を$W_{外力}$とします.
$(2\ast)$の式の位置エネルギーの変化$\Delta U$と保存力がする仕事$W_{静電気力}$の関係より
$W_{静電気力}=-\Delta U_{\rm AD}=-(-1.8)=$$1.8\rm J$
また,$(\ast)$の式のゆっくりと動かしたときの外力がした仕事$W_{外力}$と保存力がした仕事$W_{静電気力}$の関係式より
$W_{外力}=-W_{静電気力}=$$-1.8\rm J$
(2)

次に,I→Fに移動したときの位置エネルギーの変化$\Delta U_{\rm IF}$を求めよう.
$\Delta U_{\rm IF}=-2.0×(2.0-1.4)=-1.2 \rm{J}$
$(2\ast)$の式の位置エネルギーの変化$\Delta U$と保存力がする仕事$W_{静電気力}$の関係より
$W_{静電気力}=-\Delta U_{\rm IF}=-(-1.2)=$$1.2\rm J$

結局,先ほどもまとめた次のことをしっかりと理解できれば難しい問題ではないね.
丸暗記では×だよ.(すぐ忘れちゃうから)
静電気力がする仕事を$W_{静電気力}$,外力がする仕事を$W_{外力}$,位置エネルギーの変化を$\Delta U$とする.
★外力を加えて荷電粒子をゆっくりと動かす場合
$\Delta U=W_{外力}$,$W_{静電気力}+W_{外力}=0$ $\dots (\ast)$
★荷電粒子が静電気力を受けて自由に動く場合
$W_{静電気力}=-\Delta U$ $\dots (2\ast)$




コメント
[…] […]
[…] […]