
導体棒の磁場中の運動の
・速度の時間変化
・電流の時間変化
は入試でもよくみかけます.
今回からは,グラフの問題について何回かに分けて対策していきましょう.
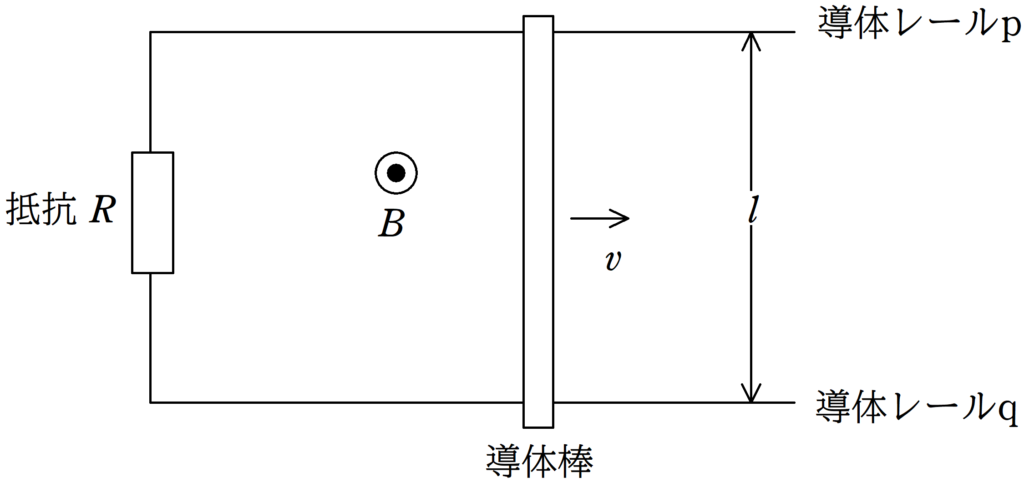
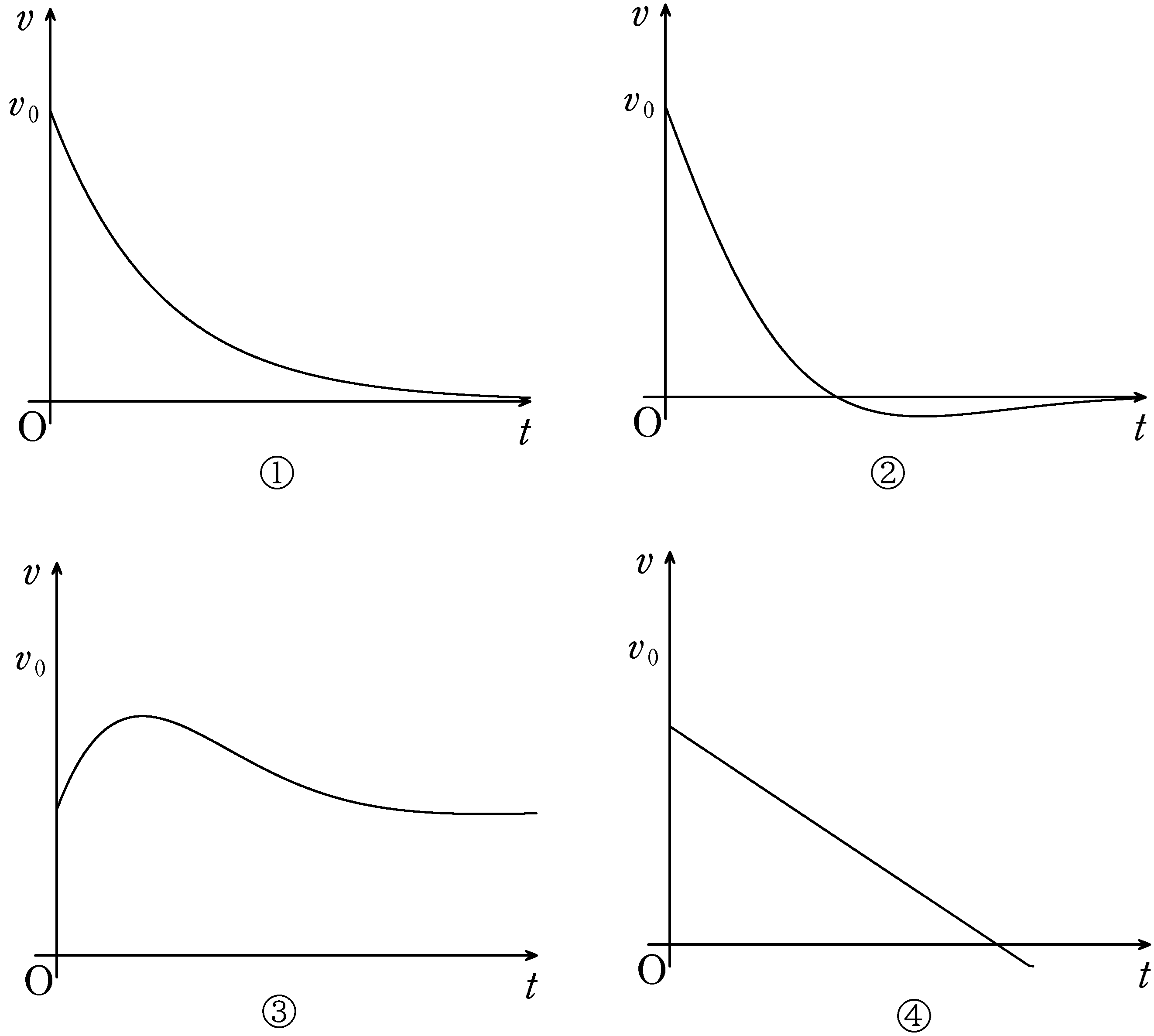
図のように,平行に固定された導体レールp,qと抵抗値$R$の抵抗と長さ$l$の導体棒を用いて回路をつくった.いま,図の奥から手前向きに一様な磁束密度$B$の磁場をかけた状態で導体棒に時刻$t=0$で右向きに大きさ$v_{0}$の初速度を与えた.このとき,導体棒の速度の時間変化として最も適当なものを,次の①~④の中から選べ.ただし,抵抗値$R$以外の抵抗は無視をし,摩擦や空気抵抗も無視をする.また,速度の正の向きは初速度の向きである.

グラフの問題は「感覚的に選ぶ」のではなく,「式を立てて考察する」癖をつけましょう.
確認すべきことは,今までの導体棒の問題と一緒です.
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は,PQの長さを$l$,PQ方向に垂直な速さを$v_{\perp}$,導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば,
$V=v_{\perp}Bl$
- 回路の式(オームの法則,コンデンサーの基本式,電荷保存則など)
- 導体棒の運動に関する式(つり合いの式,運動方程式,運動量保存則など)
- 導体棒と回路の系全体のエネルギー収支の式
★ キルヒホッフ則
下図のように,速度$v$で動いているときには,導体棒が起電力$vBl$の電池になる.流れる電流の大きさを$I$として,図の向きを正とする.キルヒホッフ則より
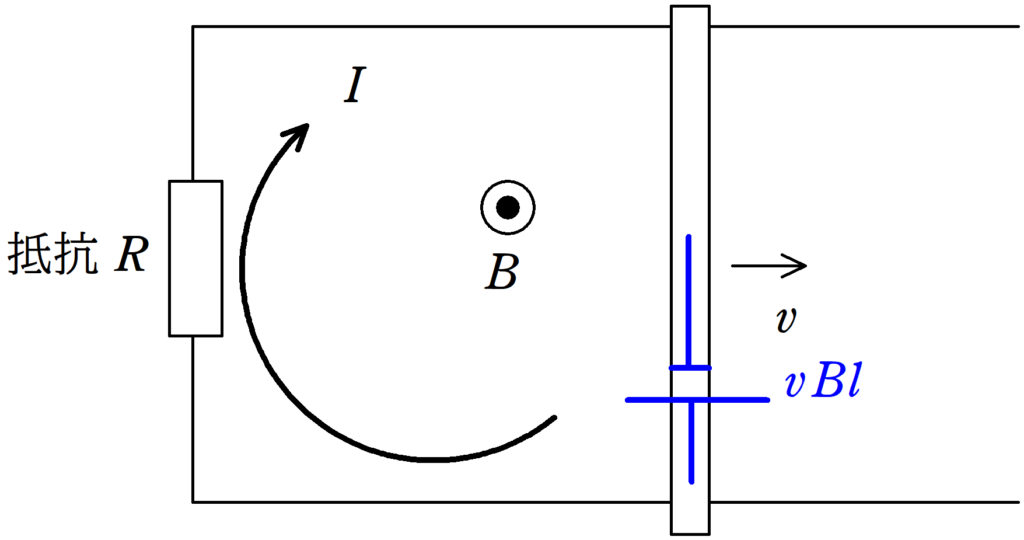
$vBl-RI=0$
$\therefore I=\dfrac{vBl}{R} \cdots (\ast)$
★ 運動方程式
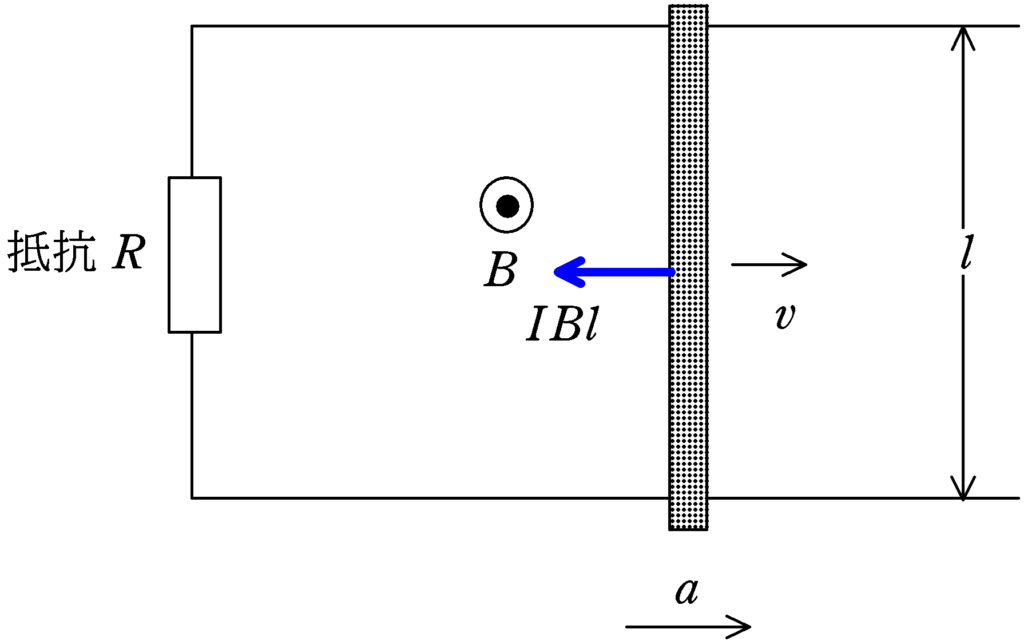
図のように,電流が上側から下側に流れるので,電磁力は左方向にはたらく.(フレミング左手の法則)その大きさは$IBl$.速度$v$のときの導体棒の加速度を$a$,導体棒の質量を$m$とすると,導体棒の運動方程式より
$ma=-IBl$ $\cdots (2\ast)$
$(\ast)$を$(2\ast)$に代入して
$ma=-\dfrac{vBl}{R}\cdot Bl=-\dfrac{B^{2}l^{2}}{R}v$

この形の運動方程式は,導体棒の問題でよく出きます.
こちらの記事でも紹介しているので,ご確認ください.
質量を$m$,加速度を$a$,速度を$v$,$C$を定数とすると
$ma=-kv+C$
は終端速度型の運動方程式である.
終端速度型の運動方程式は次の特徴がある.
十分時間が経つと,速度が一定(加速度が0)になる.
速度が一定になったときの速度を終端速度という.
終端速度は運動方程式に$a=0$を代入して
$0=-kv+C$ $\therefore v=\dfrac{C}{k}$
また,$t=0$のときの速度を$v_{0}$とすると,そのときの加速度($v-t$グラフの傾き)は
$a=\dfrac{-kv_{0}+C}{m}$
となる.

$ma=-\dfrac{B^{2}l^{2}}{R}v$ の式から
$a=-\dfrac{B^{2}l^{2}}{mR}v$
と変形したときの$v-t$グラフを考えればいいんだね.
時刻0のとき,速度が$v_{0}$だから,加速度$a_{0}$は
$a_{0}=-\dfrac{B^{2}l^{2}}{mR}v_{0} (<0)$
で,加速度が負のため,どんどん速さが小さくなります.
そして,速度の大きさが小さくなるたび,加速度の絶対値が小さくなるので,$v-t$グラフの傾きが小さくなるんだね.
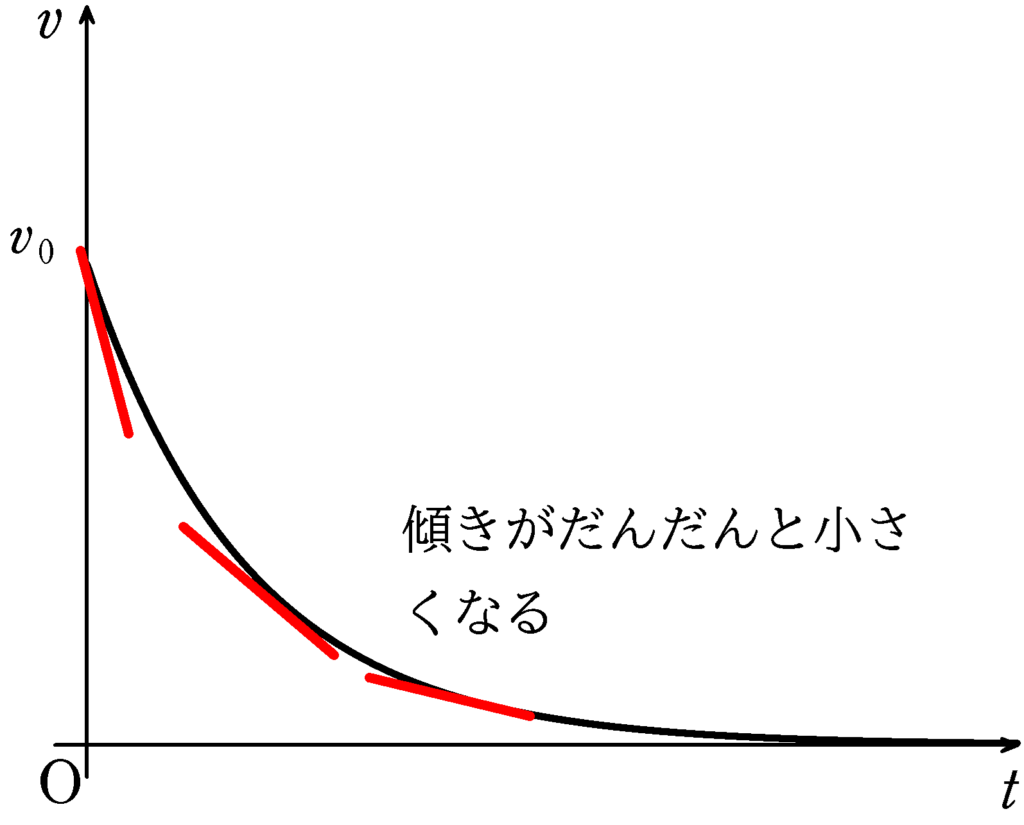

ただ,速度がどんどん小さくなるのであれば,速度がマイナスになったりするんじゃないの??

いえ,そうはなりません.
$a=-\dfrac{B^{2}l^{2}}{mR}v$
の式によれば ,$v=0$となると,$a=0$となり,加速度が0なので,速度が変化しなくなります.なので,速度がマイナスになることはありません.
(この手の運動方程式は,十分時間が経つと加速度が0になることを覚えておいてもよいです.加速度が0であって,速度が0とは限りません.)

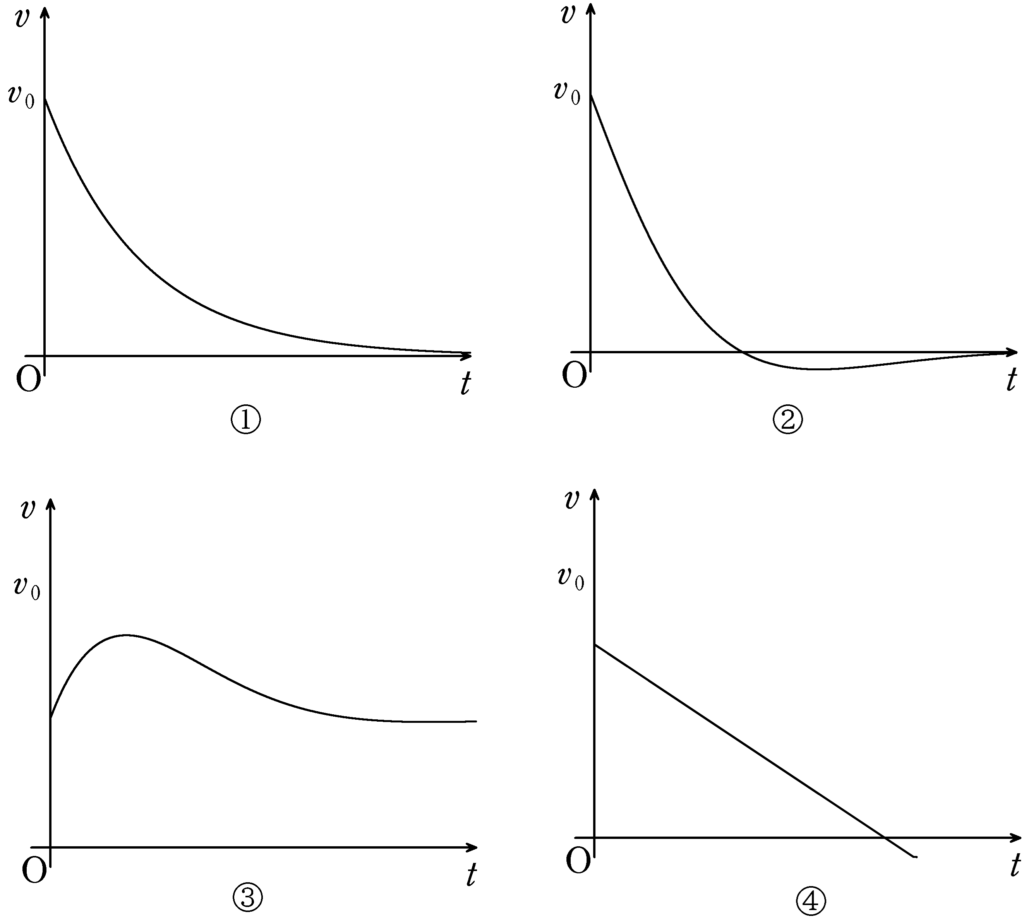
②は,速度がマイナスになっているから×だね.
③は,はじめの傾きが正なので×.
④は,一見よさそうだけど,傾き$a$は一定ではなく,速度によって変わっていくんだね.だから×.
正解は①です.



コメント
[…] 導体棒のグラフ対策1PHYさん導体棒の磁場中の運動の・速度の時間変化・電… 問題 […]