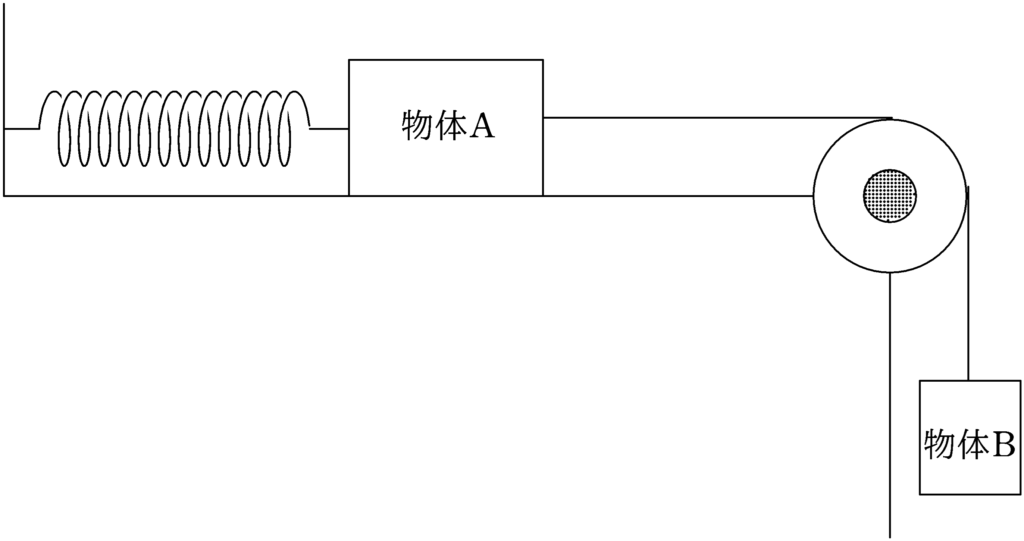
質量$M$の物体Aと質量$m$の物体Bがある.物体Aはなめらかな水平面上にあり,ばね定数$k$の軽いばねにつながれている.ばねの他端は壁に固定されている.さらに物体Aには軽くて伸びない糸がつながれており,糸は軽くて滑らかに回転する滑車を通して,物体Bにつながれている.物体Bに力を加え,ばねを自然長から$b$だけ伸ばして静かにはなしたところ,糸はたるむことなく,物体Aと物体Bは単振動をはじめた.重力加速度の大きさを$g$として,$b,m,M,g$の間に成り立つ不等式を求めよ.
<解答>

ばねが自然長になるときの物体Aの位置を原点として,ばねが伸びる方向に$x$座標をとりましょう.
今までと同様に,位置$x$における加速度を$a$として,運動方程式を立て,情報を得ます.
また,張力が$0$になるときの$x$座標もこの運動方程式を得ることができます.
張力の大きさを$S$とすると,物体Aにはたらく水平方向の力と物体Bにはたらく鉛直方向の力は次図のようになります.
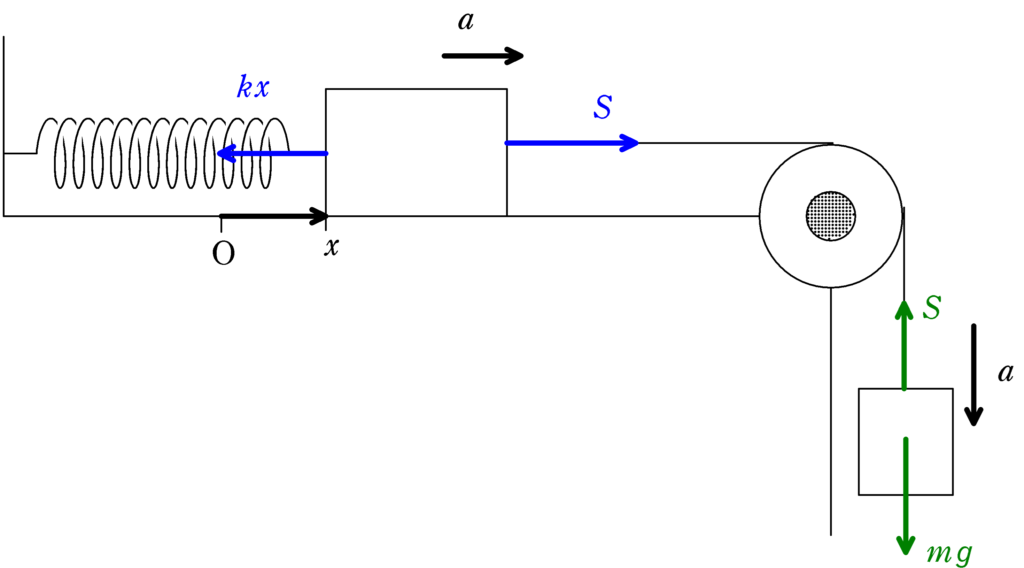
★ 運動方程式
$Ma=-kx+S \cdots (\ast)$
$ma=mg-S \cdots (2\ast)$
$(\ast)+(2\ast)$より
$\eqalign{(M+m)a&=-kx+mg\\&=-k\left(x-\dfrac{mg}{k}\right) \cdots (3\ast)}$
質量を$m$,加速度を$a$,物体の座標を$x$,$x_{0}$を定数,$k$を正の定数とする.
運動方程式が以下で表されている.
$ma=-k(x-x_{0})$
このとき,振動の中心は$x_{0}$,角振動数$\omega$と周期$T$は次のようになる.
$\omega=\sqrt{\dfrac{k}{m}}$
$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{m}{k}}$

$(3\ast)$の式より,単振動の中心は
$x=\dfrac{mg}{k}$
となります.
また,$(3\ast)$より
$a=\dfrac{-kx+mg}{M+m}$
を$(2\ast)$に代入して,$S$を求めてみましょう.
$\eqalign{S&=m(g-a)\\&=m\left\{g-\dfrac{-kx+mg}{M+m}\right\}\\&=m\left\{\dfrac{(M+m)g+kx-mg}{M+m}\right\}\\&=\dfrac{m(Mg+kx)}{M+m}}$

つまり,$S$が$0$になるときの$x$座標は
$\dfrac{m(Mg+kx)}{M+m}=0$
$\therefore$ $x=-\dfrac{Mg}{k}$
です.
自然長から$b$伸ばしたところで運動がはじまるので,ここが単振動の右端になります.中心座標が$\dfrac{mg}{k}$,張力が$0$になる場所が$-\dfrac{Mg}{k}$であることを図に書いて整理すると,次のようになります.(この図は毎回かく癖をつけましょう.)
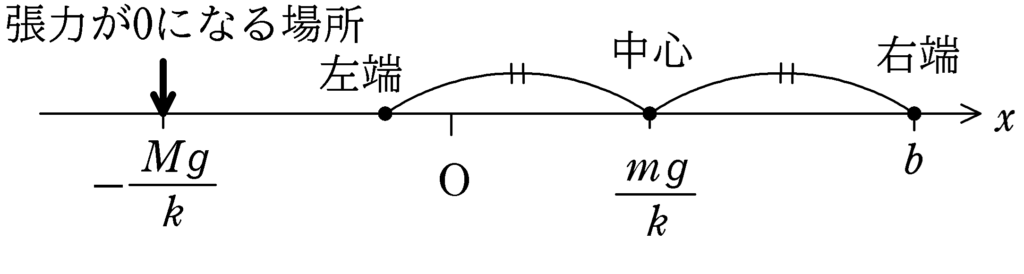

右端と中心の距離が$b-\dfrac{mg}{k}$なので,左端の位置は
$\dfrac{mg}{k}-\left(b-\dfrac{mg}{k}\right)=\dfrac{2mg}{k}-b$
となります.
糸がたるまないためには,
張力が$0$になる座標$<$単振動の左端
つまり,
$-\dfrac{Mg}{k}<\dfrac{2mg}{k}-b$
整理すると
$\dfrac{2m+M}{k}g>b$ (答)

単振動の振り幅を整理して,どのような条件のときに張力が$0$の場所にいかないかを考えていけばよいわけです.



コメント