今回は，「気体の密度」が与えられていたため，
$\dfrac{P}{\rho T}=一定$
の式を用いてきましたが，今回は
「1モルあたりの質量」
が与えられる問題を扱いたいと思います．
そのため，$\dfrac{P}{\rho T}=一定$の式ではなく，「理想気体の状態方程式」を用いた解法をとります．
まずは問題を見てみましょう．
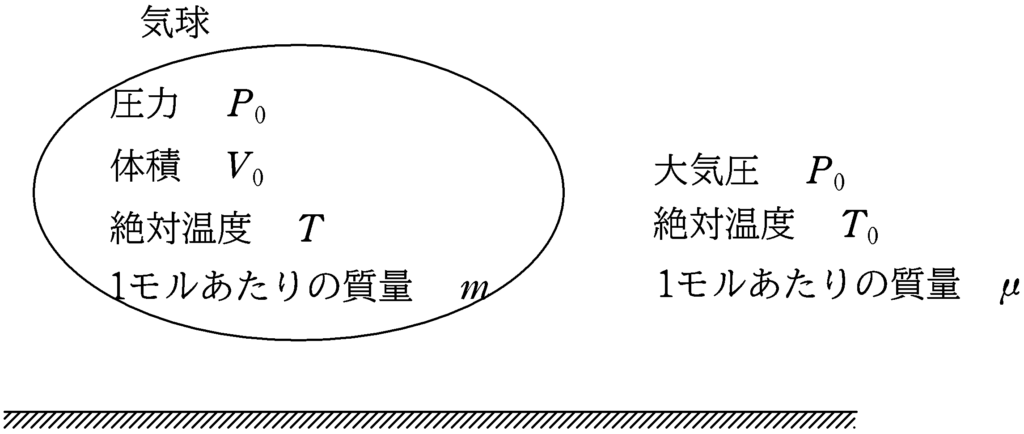
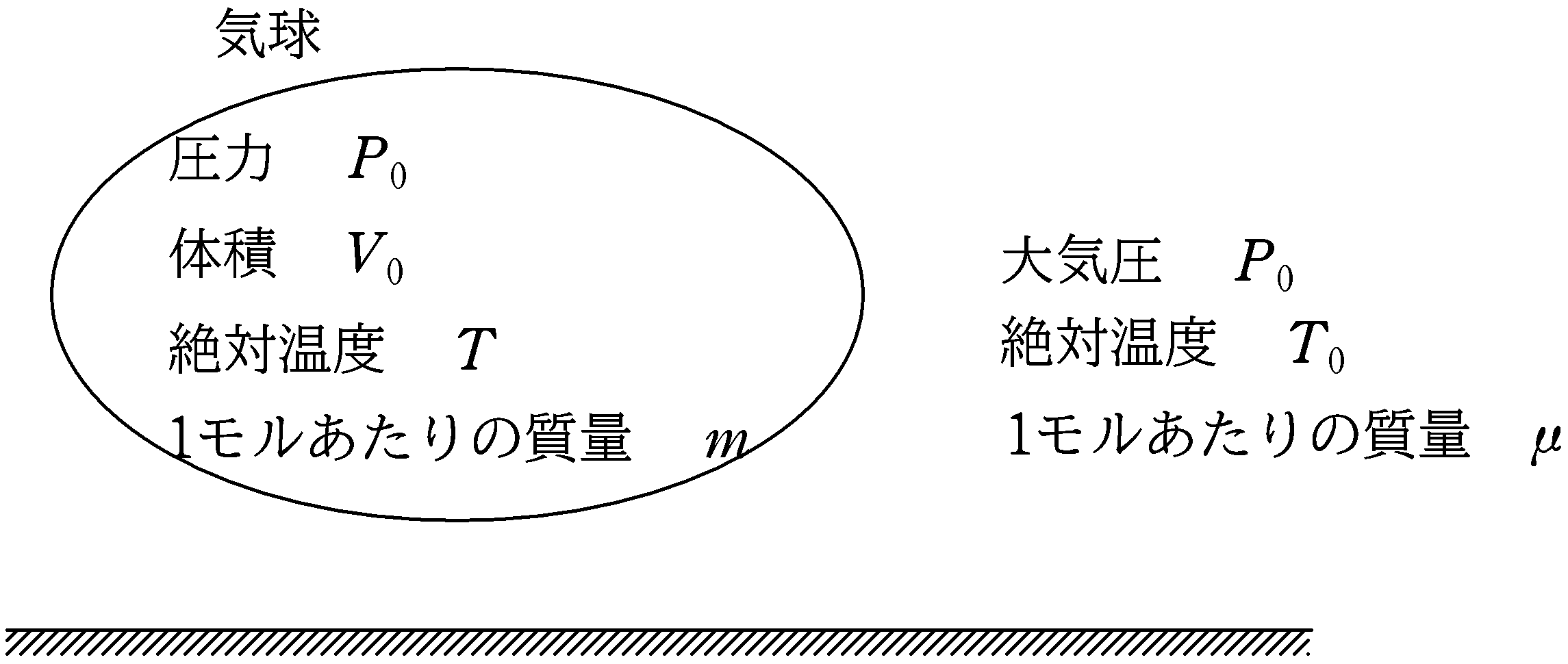
地上に質量$M$のヘリウム気球が置かれている．気球のヘリウムを入れる部分の体積は$V_{0}$である．また，地上における空気の圧力は$P_{0}$で絶対温度を$T_{0}$とする．気球内のヘリウムと地上における空気の圧力は同じである．また，ヘリウム気体の絶対温度が$T$であった．ヘリウム気体と空気は理想気体と考えることができる．ヘリウムの1モルあたりの質量を$m$，地上の空気の1モルあたりの質量を$\mu$，重力加速度の大きさを$g$，気体定数を$R$として，気球が浮かび上がるときの質量$M$の条件を求めよ．
＜解答＞
気球にはたらく力について考えます．
そのためにも，「ヘリウムの重さ」，「浮力（まわりの空気がおす力）の大きさ」を判明させる必要があるのですが，質量を計算するには，それぞれの物質量を計算する必要があります．
ちなみに，浮力はアルキメデスの原理より，「おしのけた空気の重さ」と等しいので，気球がおしのけた分の空気の物質量の計算が必要です．
理想気体の状態方程式から物質量を計算しましょう．
物体にはたらく浮力の大きさは，物体がおしのけた液体（または気体）の重さと等しい．
おしのけた液体（または気体）の密度を$\rho$，押しのけた分の物体の体積を$V$，重力加速度の大きさを$g$とすると，浮力の大きさ$F$は
$F=\rho Vg$
※ $\rho$は物体の密度ではなく，おしのけた液体（または気体）の密度である．
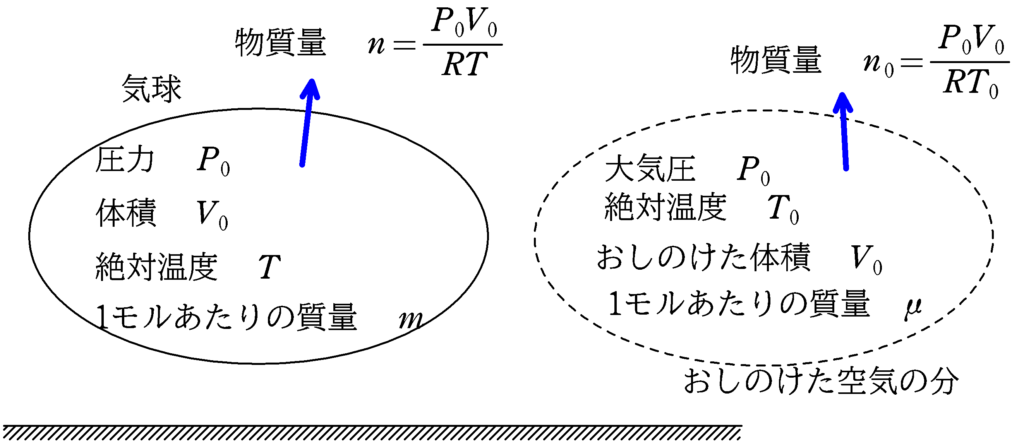
★ ヘリウム気体の状態方程式
物質量を$n$とすると
$P_{0}V_{0}=nRT$ $\therefore\,\, n=\dfrac{P_{0}V_{0}}{RT}$ $\cdots (\ast)$
★ 気球がおしのけた空気の状態方程式
物質量を$n_{0}$とすると
$P_{0}V_{0}=nRT_{0}$ $\therefore\,\, n=\dfrac{P_{0}V_{0}}{RT_{0}}$ $\cdots (2\ast)$
ヘリウムの重さは$nmg$です．
物質量が$n$で，1モルあたりの質量が$m$なので，$nm$がヘリウムの質量になるんだね．
さらに，おしのけた空気の重さが$n_{0}\mu g$です．
物質量が$n_{0}$で，1モルあたりの質量が$\mu$なので，$n_{0}\mu$がおしのけた空気の質量になるんだね．
気球が浮かび上がるための条件は
$（ヘリウム気体の重さ）+(気球の重さ)<(浮力の大きさ)$
です．この式に$(\ast)，(2\ast)$を代入し$T$を求めましょう．
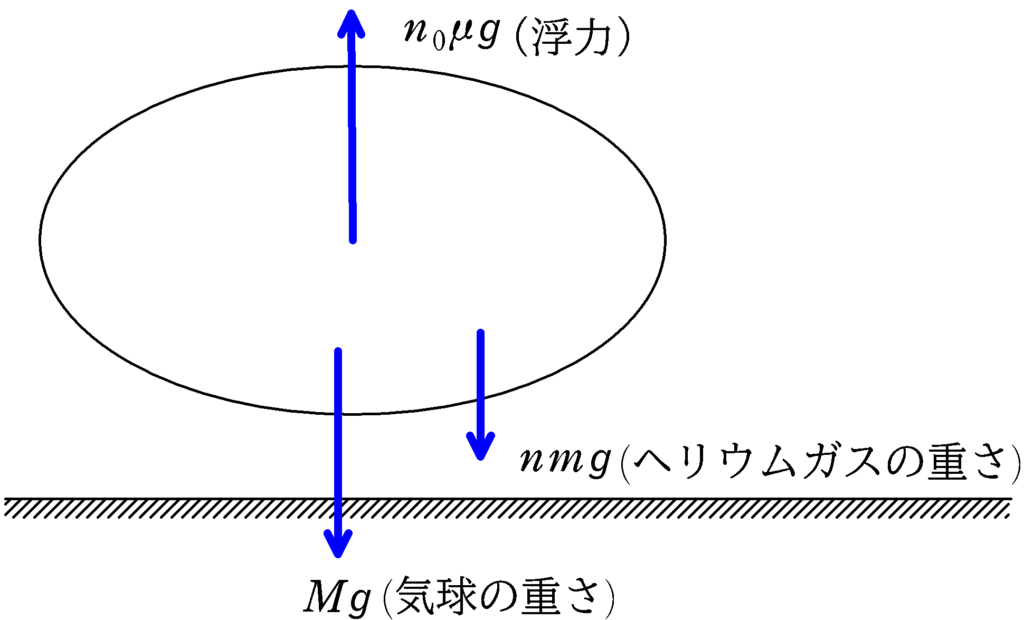
★ 気球が浮かぶ条件
$nmg+Mg<n_{0}\mu g$
$\therefore\,\, nm+M<n_{0}\mu$
$(\ast)，(2\ast)$を代入して
$\dfrac{P_{0}V_{0}}{RT}\times m+M<\dfrac{P_{0}V_{0}}{RT_{0}}\times \mu$
$\therefore\,\, M<\dfrac{P_{0}V_{0}}{R}\left(\dfrac{\mu}{T_{0}}-\dfrac{m}{T}\right)$ (答)
コメント