
前回の内容はこちらです.

前回までは,「気体の密度」が与えられていたため,
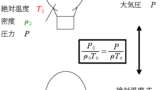
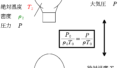
$\dfrac{P}{\rho T}=一定$
の式を用いてきましたが,今回は
「1モルあたりの質量」
が与えられる問題を扱いたいと思います.
そのため,$\dfrac{P}{\rho T}=一定$の式ではなく,「理想気体の状態方程式」を用いた解法をとります.
まずは問題を見てみましょう.
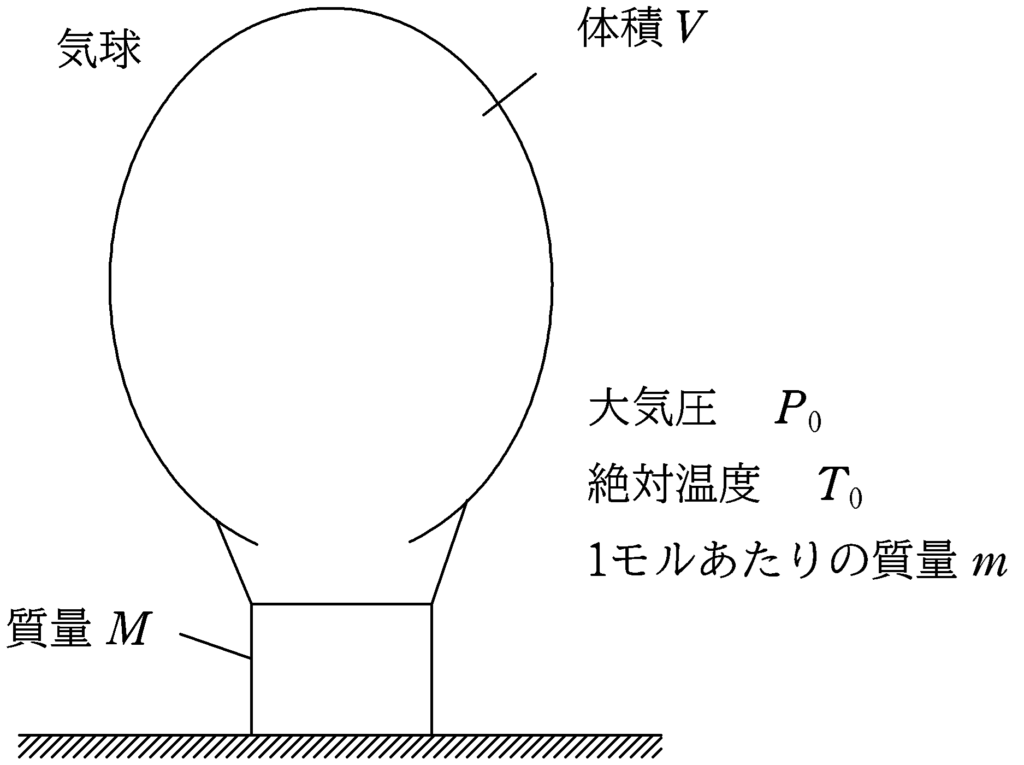
地上に質量$M$の熱気球が置かれている.熱気球の空気を入れる部分の体積は$V$である.また,地上における空気の絶対温度を$T_{0}$とする.熱気球内の空気と地上における空気は自由に出入りできるようになっているため,気球内の圧力は地上の圧力と同じである.以下,空気は理想気体と考えることができる.熱気球内の空気を熱していくと,絶対温度が$T$になったときに気球は浮かび上がった.地上の空気の1モルあたりの質量を$m$,重力加速度の大きさを$g$,気体定数を$R$として,浮かびあがったときの絶対温度$T$を求めよ.
<解答>

今回は「1モル」あたりの質量が与えられています.
1モルあたりの質量が$m$なので,物質量がわかれば
$(物質量)\times m$
が全体の質量となります.
熱気球のつり合いを考える際に熱気球内の空気の重さと熱気球のはたらく浮力(まわりの空気が気球を押す力)が必要になってきます.
熱気球内の重さを求めるために,熱気球内の物質量$n$モルを求め,熱気球にはたらく浮力の大きさを求めるために,「熱気球がおしのけたまわりの空気」の物質量$n_{0}$モルを求めます.
ちなみに,浮力はアルキメデスの原理を利用して求めましょう.
物体にはたらく浮力の大きさは,物体がおしのけた液体(または気体)の重さと等しい.
おしのけた液体(または気体)の密度を$\rho$,押しのけた分の物体の体積を$V$,重力加速度の大きさを$g$とすると,浮力の大きさ$F$は
$F=\rho Vg$
※ $\rho$は物体の密度ではなく,おしのけた液体(または気体)の密度である.
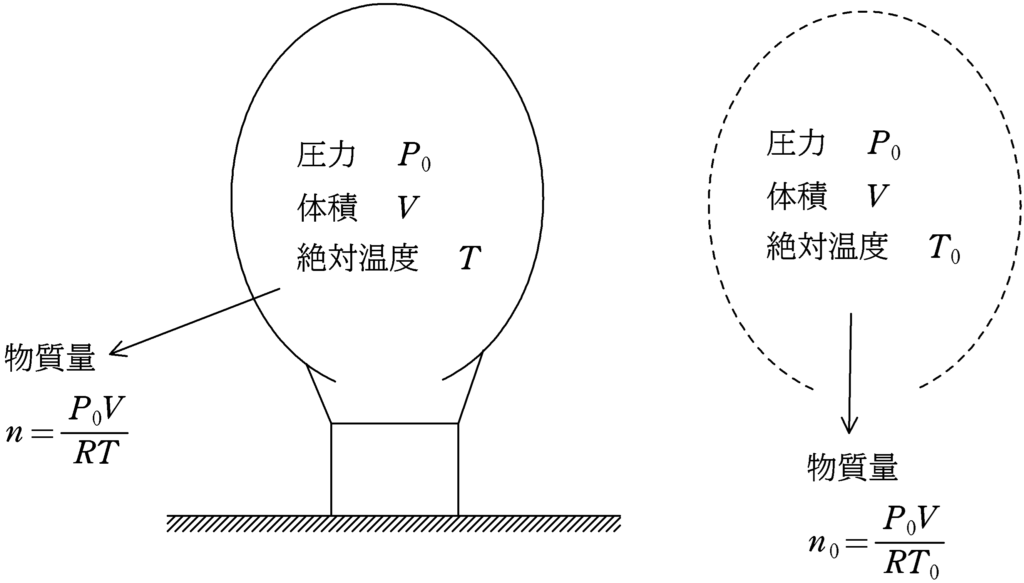

熱気球内の空気の圧力は外の圧力と同じ$P_{0}$で体積が$V$,絶対温度が$T$なので,理想気体の状態方程式から物質量$n$が計算できるね.
$P_{0}V=nRT$ $\therefore n=\dfrac{P_{0}V}{RT}$ $\cdots (\ast)$
また,気球がおしたのけた分の空気の重さは圧力が$P_{0}$,体積が$V$,絶対温度が$T_{0}$なので,理想気体の状態方程式から物質量$n_{0}$の計算ができます.
$P_{0}V=n_{0}RT_{0}$ $\therefore\,\, n_{0}=\dfrac{P_{0}V}{RT_{0}}$ $\cdots (2\ast)$
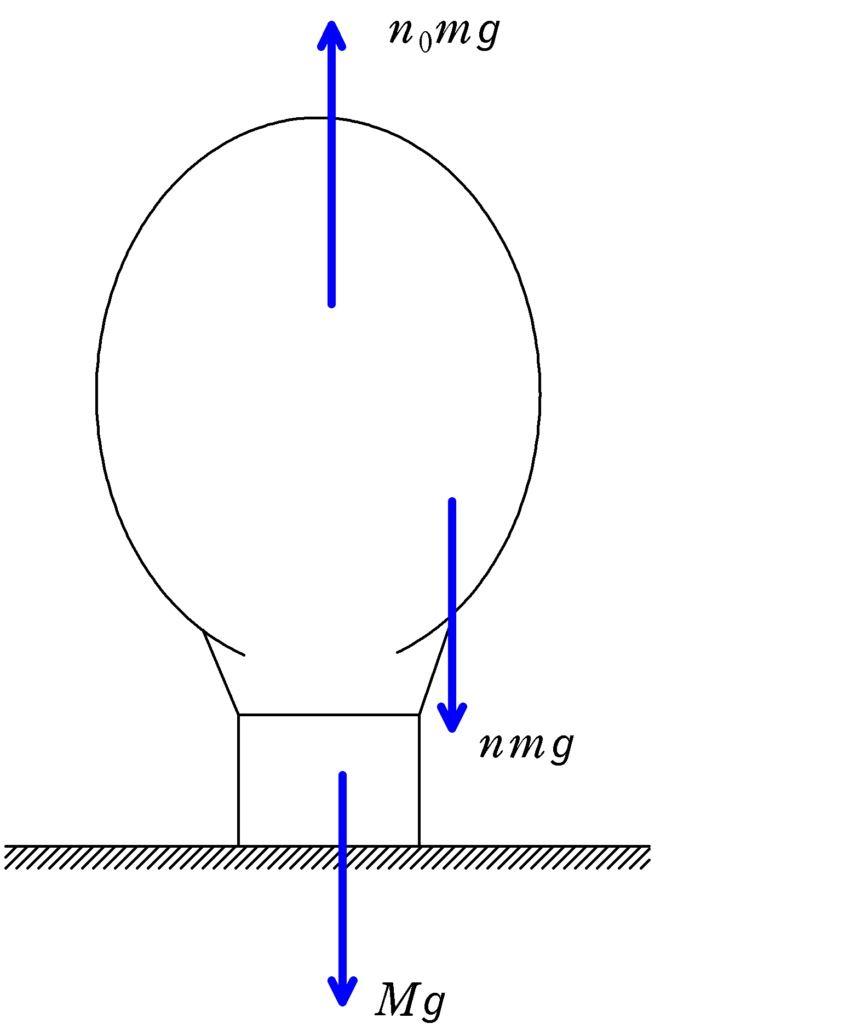

気球自体の重さは$Mg$,熱気球内の重さは物質量が$n$のとき,$nm$が質量となるので,重さは$nmg$.おしのけた空気の物質量が$n_{0}$のとき,$n_{0}m$ががおしのけた空気の質量なので,浮力の大きさは$n_{0}mg$となります.
つり合いの式を立て,$(\ast),(2\ast)$を代入しましょう.
★ 気球のつり合いの式
$nmg+Mg=n_{0}mg$
$\therefore\,\, nm+M=n_{0}m$
$(\ast),(2\ast)$を代入して
$\dfrac{P_{0}V}{RT}\times m+M=\dfrac{P_{0}V}{RT_{0}}\times m$
$\therefore\,\, T=\dfrac{P_{0}VmT_{0}}{P_{0}Vm-MRT_{0}}$ (答)


コメント