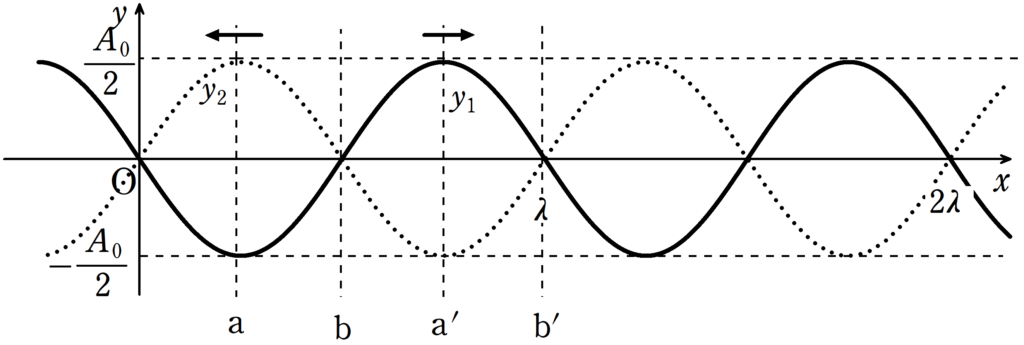
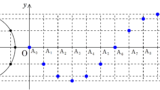
一般に，定常波は波長も振幅も等しい逆向きに進む2つの正弦波が重なり合って生じる．上図は，時刻$t=0$の瞬間の右に進む正弦波の変位$y_{1}$（実線）と左に進む正弦波の変位$y_{2}$（破線）を，位置$x$の関数として表したグラフである．それぞれの振幅を$\dfrac{A_{0}}{2}$，波長を$\lambda$，振動数を$f$とすれば，時刻$t$における$y_{1}$は
$y_{1}=\dfrac{A_{0}}{2}\sin 2\pi(ft-\dfrac{x}{\lambda})$
と表される．このとき，次の問いに答えよ．
(1) 時刻$t$における$y_{2}$を$A_{0}$，$f$，$t$，$x$，$\lambda$を用いて表せ．
(2) $\rm a$，$\rm a^{\prime}$，$\rm b$，$\rm b^{\prime}$の中から節の位置となるものをすべて選べ．
<解答>
(1)
そもそも，なぜ$y_{1}$が
$y_{1}=\dfrac{A_{0}}{2}\sin 2\pi(ft-\dfrac{x}{\lambda})$
となるのかを考えてみましょう．
これを調べるには，$y_{1}$の原点の振動をみていきます．
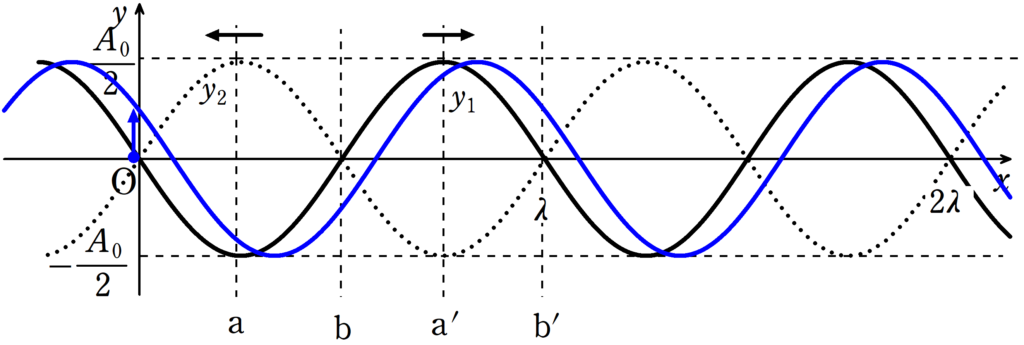
$y_{1}$の波は右に進んでいます．
次の瞬間の波（青色の波）をかいて，原点部分に着目すると，$t=0$では中心にあった媒質が次の瞬間$y$の正方向に移動しています．
$0$から正の方向に移動する振動は$\sin$型です．
振動数が$f$なので，$y_{1}$の原点の振動の時間変化$y_{1}(0)$は
$y_{1}(0)=\dfrac{A_{0}}{2}\sin 2\pi ft $
となります．
波とは，振動が遅れて伝わる現象です．
波の伝わる速さを$v$とすれば，位置$x$の振動は時間$\dfrac{x}{v}$前の原点での振動と同じです．
位置$x$の媒質の振動の式を$y_{1}(x)$とすると
$\eqalign{y_{1}(x)&=\dfrac{A_{0}}{2}\sin 2\pi f(t-\dfrac{x}{v})\\&=\dfrac{A_{0}}{2}\sin 2\pi(ft-\dfrac{fx}{v})\\&=\dfrac{A_{0}}{2}\sin 2\pi(ft-\dfrac{x}{\lambda})}$
途中，波の基本式（$v=f\lambda$）を使いました．
同じように$y_{2}$の原点での振動を考えます．
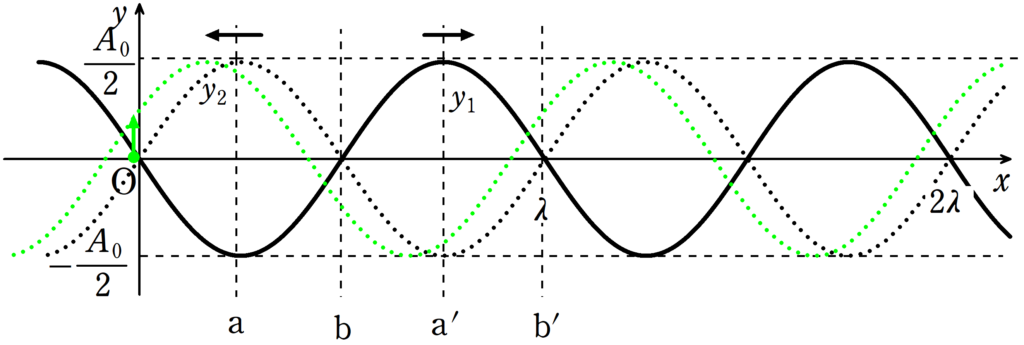
$y_{2}$の次の瞬間の波をかくと，原点での振動が$\sin$型であることが確認できます．
$y_{2}$の波は$x$軸の負の方向に進んでいます．したがって，
$x(>0)$での振動は時間$\dfrac{x}{v}$後の原点での振動と同じなので，$y_{2}(x)$は
$\eqalign{y_{2}(x)&=\dfrac{A_{0}}{2}\sin 2\pi f(t+\dfrac{x}{v})\\&=\dfrac{A_{0}}{2}\sin 2\pi (ft+\dfrac{fx}{v})\\&=\dfrac{A_{0}}{2}\sin 2\pi (ft+\dfrac{x}{\lambda})}$ (答)
(2)
(1)で考察したように，原点での$y_{1}$と$y_{2}$の振動はピッタリです．
振動のタイミングが同じ場所は大きな振動をします．
そして，この場所が定常波の腹となります．
腹と節の距離が$\dfrac{\lambda}{4}$であることを用いれば，節の場所は$\rm a$と$\rm a^{\prime}$です．
たしかに，この場所は$y_{1}$と$y_{2}$の振動が真反対で，打ち消し合います．
答え $\rm a$と$\rm a^{\prime}$
コメント