[ベリリウム線の正体]中性子の発見[2021年　同志社大（一部）]

＜解答＞

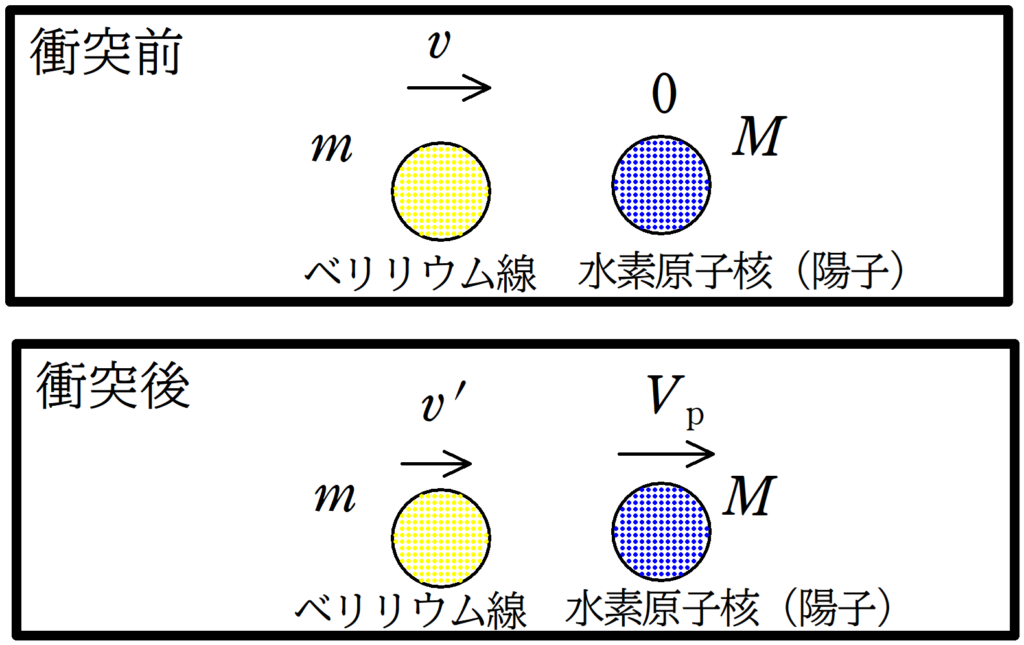
★　運動量保存則

$mv+M\cdot 0=mv^{\prime}+MV_{\rm p}$　$\dots　(\ast)$

★　反発係数の式

$1=-\dfrac{v^{\prime}-V_{\rm p}}{v-0}$

$\therefore$　$v^{\prime}=V_{\rm p}-v$　$\dots　(2\ast)$

$(\ast)$，$(2\ast)$より，$v^{\prime}$を消去すると

$\eqalign{mv&=m(V_{\rm p}-v)+MV_{\rm p}\cr (M+m)V_{\rm p}&=2mv\cr V_{\rm p} &=\dfrac{2m}{M+m}v　 (\clubsuit)}$

したがって，$\fbox{ カ }$$\dfrac{2m}{M+m}v$(答)

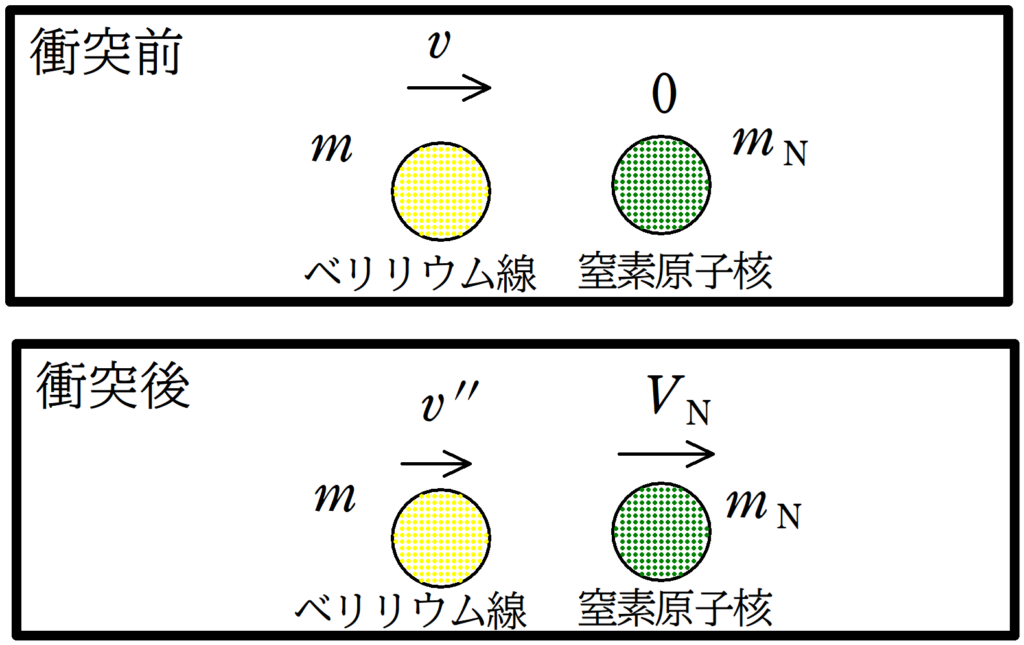
★　運動量保存則

$mv+m\cdot 0=mv^{\prime\prime}+m_{\rm N}V_{\rm N}$

★　反発係数の式

$1=-\dfrac{v^{\prime\prime}-V_{\rm N}}{v-0}$

以上2式を$V_{\rm p}$を計算したときと同様に，$v^{\prime\prime}$を消去すると

$V_{\rm N}=\dfrac{2m}{m_{\rm N}+m}v$　$\dots　(\heartsuit)$

$(\clubsuit)$と$(\heartsuit)$より

$\eqalign{\dfrac{V_{\rm p}}{V_{\rm N}}&=\dfrac{\dfrac{2m}{M+m}v}{\dfrac{2m}{m_{\rm N}+m}v}\\&=\dfrac{m_{\rm N}+m}{M+m}}$

陽子の質量数は$1$，窒素原子核の質量数は$14$なので，$m_{\rm N}=14M$したがって

$\eqalign{\dfrac{V_{\rm p}}{V_{\rm N}}&=\dfrac{14M+m}{M+m}\\&=\dfrac{14+\dfrac{m}{M}}{1+\dfrac{m}{M}}\\&=\dfrac{14+k}{1+k}}$

（途中問題文で与えられた$k=\dfrac{m}{M}$を用いた）

$\eqalign{\dfrac{\dfrac{1}{2}MV_{\rm p}^{2}}{\dfrac{1}{2}m_{\rm N}V_{\rm N}^{2}}&=\dfrac{5.60}{1.40}\cr\dfrac{MV_{\rm p}^{2}}{m_{\rm N}V_{\rm N}^{2}}&=4\cr \dfrac{V_{\rm p}^{2}}{V_{\rm N}^{2}}&=\dfrac{4m_{\rm N}}{M}}$

さらに，$m_{\rm N}=14M$より

$\eqalign{\left(\dfrac{V_{\rm p}}{V_{\rm N}}\right)^{2}&=\dfrac{4\cdot 14M}{M}\\&=56}$

$\therefore$　$\dfrac{V_{\rm p}}{V_{\rm N}}=2\sqrt{14}$

$\fbox{ キ }$で求めた$\dfrac{V_{\rm p}}{V_{\rm N}}=\dfrac{14+k}{1+k}$であることから

$\eqalign{\dfrac{14+k}{1+k}&=2\sqrt{14}\cr \ 14+k &=2\sqrt{14}(1+k)\cr(2\sqrt{14}-1)k&=2(7-\sqrt{14})\cr k&=\dfrac{2(7-\sqrt{14})}{2\sqrt{14}-1}\cr k&=\dfrac{2(13\sqrt{14}-21)}{55}}$