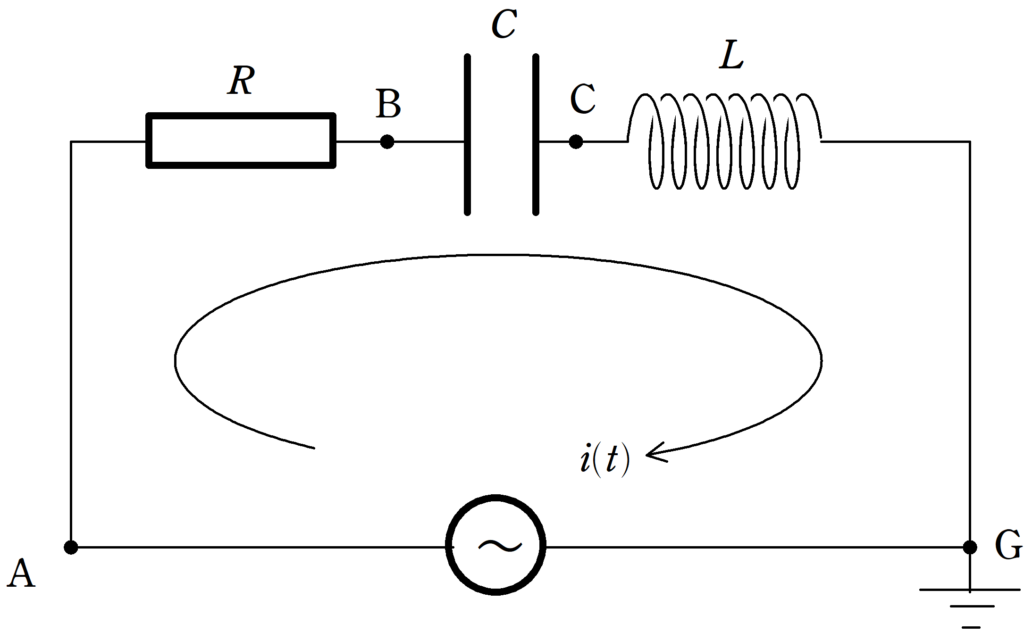
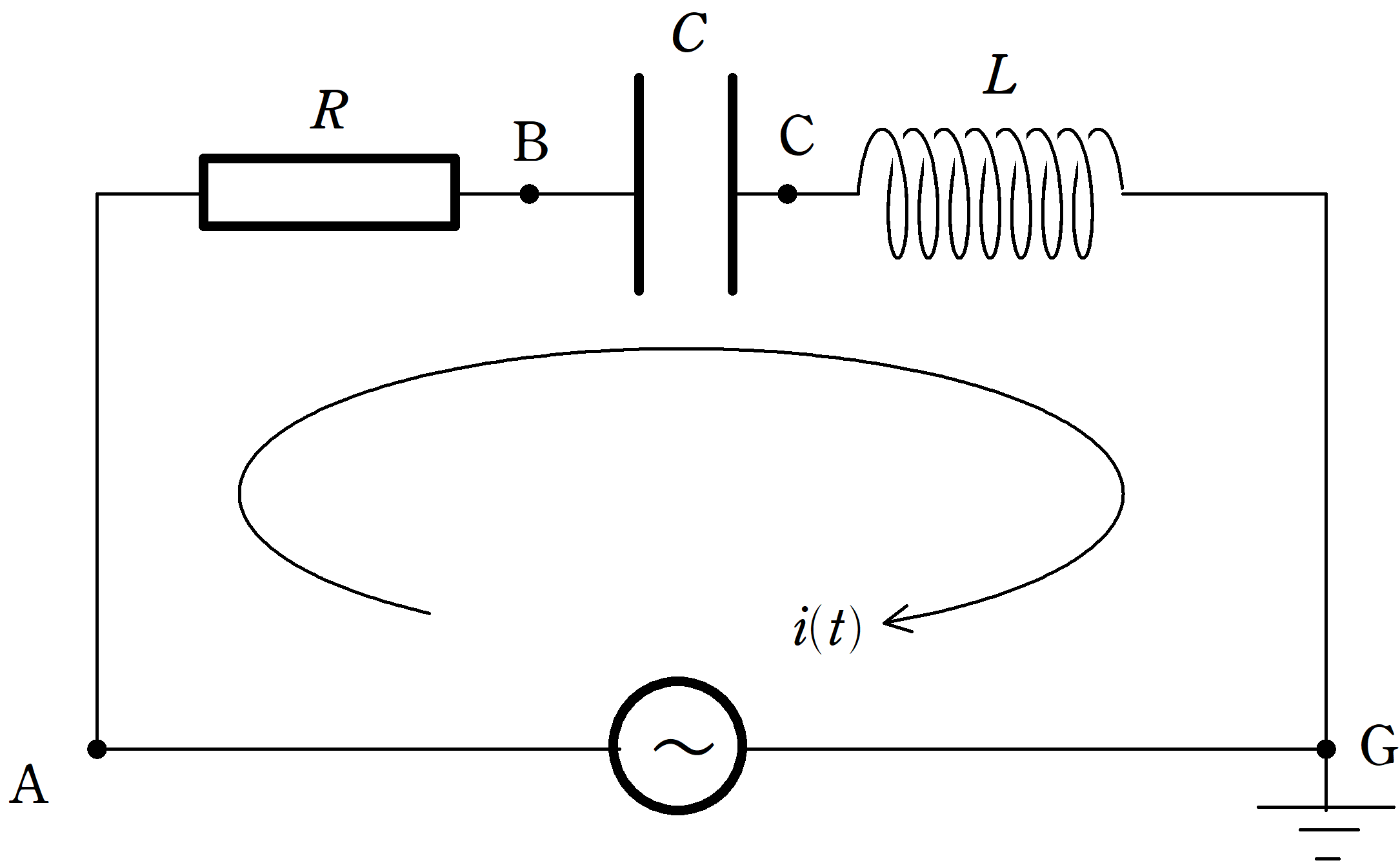
上図のように,抵抗値$R$抵抗の抵抗と,電気容量$C$のコンデンサー,自己インダクタンス$L$のコイルを直列に交流電源とつないだ.時刻$t$において,回路に流れている電流が上図の矢印の向きを正として,$i(t)=i_{0}\sin\omega t$であるとする.ただし,$i_{0}>0$であり,$\omega$は角周波数である.
(1) Bに対するAの電位$V_{\rm R}$を求めよ.
(2) Cに対するBの電位$V_{\rm C}$を求めよ.
(3) Gに対するCの電位$V_{\rm L}$を求めよ.
(4) Gに対するAの電位$V(t)$を求めよ.
(5) 回路のインピーダンス$Z$を求めよ.
(6) 回路に流れる電流の位相と電源にかかる電圧の位相のずれがないときの角周波数$\omega_{0}$を求めよ.
<解答>

交流問題は,位相のずれと最大値に着目します.
● 最大値について
回路素子にかかる電圧の最大値を$V_{0}$,流れる電流の最大値を$I_{0}$,リアクタンス(または抵抗)を$Z$とする.
このとき,次の関係が成り立つ.
$V_{0}=ZI_{0}$
$Z$は回路素子できまる.各周波数を$\omega$として
抵抗値$R$の抵抗のとき,$Z=R$
電気容量$C$のコンデンサーのとき,$Z=\dfrac{1}{\omega C}$
自己インダクタンス$L$のコイルのとき,$Z=\omega L$
● 位相のずれについて
1)電圧に対する電流の位相のずれ
抵抗:位相のずれはなし(オームの法則がいつでも成り立つ)
コンデンサー:$\dfrac{\pi}{2}$進む(電流が先に変化し,遅れて電荷が変化する)
コイル:$\dfrac{\pi}{2}$遅れる(電圧が先に変化し,遅れて電流が変化する)
2)電流に対するで電圧の位相のずれ
抵抗:位相のずれはなし(オームの法則がいつでも成り立つ)
コンデンサー:$\dfrac{\pi}{2}$遅れる(電流が先に変化し,遅れて電荷が変化する)
コイル:$\dfrac{\pi}{2}$進む(電圧が先に変化し,遅れて電流が変化する)
(1)

抵抗に電流$i(t)$が流れていることがわかっています.
このとき,抵抗にかかる電圧の位相は電流の位相と同じです.
また,電圧の最大値$V_{\rm R0}$は
$V_{\rm R0}=Ri_{0}$
から求めることができます.
$\eqalign{V_{R}&=V_{\rm R0}\sin\omega t\\&=Ri_{0}\sin\omega t}$ (答)
(2)

コンデンサーの電圧は電流に対して$\dfrac{\pi}{2}$遅れます.
コンデンサーの式$Q=CV$は瞬間々々成り立ちます.
つまり,$Q$と$V$の位相は同じです.
一方,交流回路において,電流は電荷より先に変化します.
電流が流れてから電荷が変化するのです.
また,電圧の最大値$V_{\rm C0}$は
$V_{\rm C0}=\dfrac{1}{\omega C}i_{0}$
を満たします.
$\eqalign{V_{C}&=V_{\rm C0}\sin(\omega t-\dfrac{\pi}{2})\\&=-\dfrac{i_{0}}{\omega C}\cos \omega t}$ (答)
(3)

コイルにかかる電圧は電流に対して$\dfrac{\pi}{2}$進みます.
さらに,誘導リアクタンスが$\omega L$なので,コイルにかかる電圧の最大値$V_{\rm L0}$は
$V_{\rm L0}=\omega Li_{0}$
となります.
$\eqalign{V_{L}&=V_{\rm L0}\sin(\omega t+\dfrac{\pi}{2})\\&=\omega Li_{0}\cos \omega t}$ (答)
(4)

キルヒホッフ則より,Gに対するAの電位を求めます.
$\eqalign{V(t)&=V_{\rm R}+V_{\rm C}+V_{\rm L}\\&=Ri_{0}\sin\omega t-\dfrac{i_{0}}{\omega C}\cos\omega t+\omega L\cos\omega t\\&=Ri_{0}\sin\omega t+\left(\omega L-\dfrac{1}{\omega C}\right)i_{0}\cos\omega t}$ (答)
(5)

三角関数の合成を使って(4)で得た式を変形しましょう.
$V(t)=i_{0}\sqrt{R^{2}+\left(\omega L-\dfrac{1}{\omega C}\right)^{2}}\sin(\omega t+\phi )$
ただし,
$\tan\phi =\dfrac{\omega L-\dfrac{1}{\omega C}}{R}$
したがって,電圧の最大値$V_{0}$は
$V_{0}=\sqrt{R^{2}+\left(\omega L-\dfrac{1}{\omega C}\right)^{2}} i_{0}$
回路全体にかかる電圧の最大値を$V_{0}$,電流の最大値を$I_{0}$とするとき,インピータンス$Z$は次のように決める.
$Z=\dfrac{V_{0}}{I_{0}}$

インピーダンスの定義より,
$Z=\sqrt{R^{2}+\left(\omega L-\dfrac{1}{\omega C}\right)^{2}}$ (答)
となります.
(6)

電流と電圧の位相差がない条件は(5)で出てきた$\phi$が0になることです.
すなわち
$\tan\phi=0$
$\tan\phi =\dfrac{\omega L-\dfrac{1}{\omega C}}{R}$より
$\eqalign{\omega_{0}L-\dfrac{1}{\omega_{0}C}&=0\cr \omega_{0}^{2}&=\dfrac{1}{LC}\cr \omega_{0}&=\dfrac{1}{\sqrt{LC}}}$ (答)

コメント