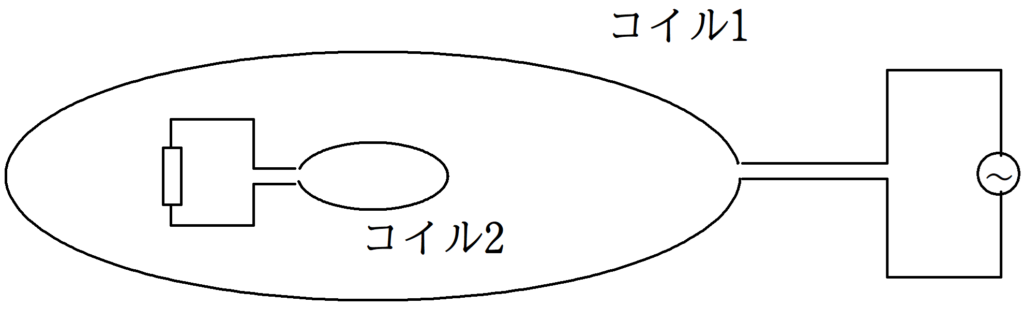
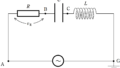
図に示すように,半径$a[\rm m]$の円形コイル1が水平に固定されている.その中心を同じにして半径$b[\rm m]$の円形コイル2を円形コイル1と同一水平面上に固定する.$b$は$a$より十分小さく,コイル2を貫く磁束は均一とみなせるものとする.また,コイル2が作る磁場(磁界),コイル以外の回路が作る磁場は無視できるとする.これらのコイルが置かれた場所での透磁率を$\mu_{0}[\rm N/A^{2}]$,円周率を$\pi$とする.
(1) コイル2を貫く磁束$[\rm Wb]$はコイル1を流れる電流$[\rm A]$に比例し,その比例係数$M[\rm H]$は相互インダクタンスとよばれる.$M$を求めよ.
(2) コイル1に時刻$t[\rm s]$における起電力$V=V_{0}\sin\omega t [\rm V]$で表される交流電源を接続した.ただし,$\omega$は角周波数$[\rm rad/s]$である.コイル2には磁場によって変化しない抵抗$R[\Omega]$を接続した.コイル1の自己インダクタンスを$L[\rm H]$とし,コイル2の自己インダクタンスは無視できるとする.設問(1)で求めた相互インダクタンスを$M$とする.このときの,コイル2を流れる電流の振幅$[\rm A]$を$M$,$V_{0}$,$R$,$L$を用いて表せ.
<解答>
(1)

円形コイル1に電流を流すとコイル1内部に磁場をつくります.
円形電流が中心につくる磁場の公式を確認しておきましょう.

半径$r[\rm m]$の円形コイルに大きさ$i[\rm A]$の電流が流れているとき,コイルの中心の磁場の大きさ$H[\rm A/m]$は次のようになる.
$H=\dfrac{i}{2r}$
磁場の向きは右ねじの法則にしたがう.
注意:中心の磁場であって,その他の部分はこの公式で表すことができない.

本来なら,上の公式は中心でしか使えない公式ですが,問題文に「$b$は$a$より十分小さく,コイル2を貫く磁束は均一とみなせるものとする.」と書かれているので,この条件を使いましょう.
磁束密度$B[\rm Wb/m^{2}]$と磁場$H[\rm A/m]$は,透磁率を$\mu[\rm N/A^{2}]$とすると
$B=\mu H$
の関係がある.
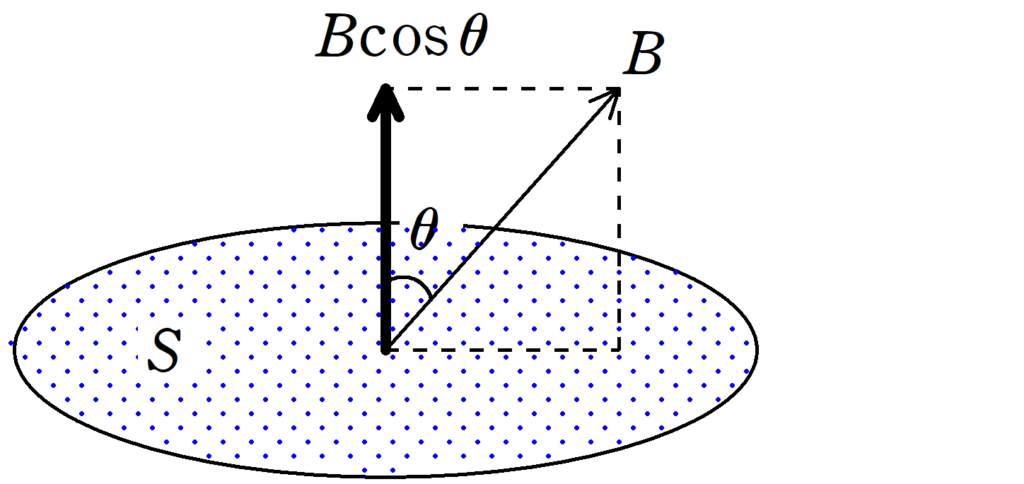
上図のように,面積$S[\rm m^{2}]$の部分を磁束密度の大きさ$B[\rm Wb/m^{2}]$の磁場が面に垂直な線に対して$\theta$の方向にかかっているとき,この面を貫く磁束$\varPhi$は
$\eqalign{\varPhi&=(B\cos\theta)S\\&=BS\cos\theta}$
となる.

このことから,コイル1に電流$I_{1}$が流れたときのコイル2を貫く磁束$\varPhi_{2}$を調べてみましょう.
★ コイル1に流れる電流$I_{1}$が中心に作る磁場$H_{1}$
$H_{1}=\dfrac{I_{1}}{2a}$
★ コイル1に流れる電流$I_{1}$が中心に作る磁束密度$B_{1}$
$\eqalign{B_{1}&=\mu_{0}H_{1}\\&=\mu_{0}\cdot \dfrac{I_{1}}{2a}\\&=\dfrac{\mu_{0}I_{1}}{2a}}$
★ コイル2を貫く磁束$\varPhi_{2}$
問題文の条件より,コイル1が中心につくる磁場はコイル2内ではどこも同じであるとみなしてよいので,
$\eqalign{\varPhi_{2}&=B_{1}\cdot \pi b^{2}\\&=\dfrac{\mu_{0}I_{1}}{2a}\cdot \pi b^{2}\\&=\dfrac{\pi \mu_{0}b^{2}}{2a}I_{1}}$

さらに,問題文に
「コイル2を貫く磁束$[\rm Wb]$はコイル1を流れる電流$[\rm A]$に比例し,その比例係数$M[\rm H]$は相互インダクタンスとする.」
と書かれているので,相互インダクタンス$M$は
$M=\dfrac{\pi \mu_{0}b^{2}}{2a}$ (答)
(2)

コイル1に$V=V_{0}\sin\omega t[\rm V]$の電圧をかけると,コイル1に電流が流れます.
交流では,最大値と位相に着目しましょう.
● 最大値について
回路素子にかかる電圧の最大値を$V_{0}$,流れる電流の最大値を$I_{0}$,リアクタンス(または抵抗)を$Z$とする.
このとき,次の関係が成り立つ.
$V_{0}=ZI_{0}$
$Z$は回路素子できまる.各周波数を$\omega$として
抵抗値$R$の抵抗のとき,$Z=R$
電気容量$C$のコンデンサーのとき,$Z=\dfrac{1}{\omega C}$
自己インダクタンス$L$のコイルのとき,$Z=\omega L$
● 位相のずれについて
1)電圧に対する電流の位相のずれ
抵抗:位相のずれはなし(オームの法則がいつでも成り立つ)
コンデンサー:$\dfrac{\pi}{2}$進む(電流が先に変化し,遅れて電荷が変化する)
コイル:$\dfrac{\pi}{2}$遅れる(電圧が先に変化し,遅れて電流が変化する)
2)電流に対するで電圧の位相のずれ
抵抗:位相のずれはなし(オームの法則がいつでも成り立つ)
コンデンサー:$\dfrac{\pi}{2}$遅れる(電流が先に変化し,遅れて電荷が変化する)
コイル:$\dfrac{\pi}{2}$進む(電圧が先に変化し,遅れて電流が変化する)

コイル1に流れる電流の最大値$I_{0}(>0)$は,次の関係を満たします.
$\eqalign{|V_{0}|&=\omega LI_{0}\cr I_{0}&=\dfrac{|V_{0}|}{\omega L}}$ $\dots (\ast)$
さらに,コイルに流れる電流は電圧に対して$\dfrac{\pi}{2}$遅れます.
したがって,コイル1に流れる電流$i_{1}$は
$\eqalign{i_{1}&=I_{0}\sin(\omega t-\dfrac{\pi}{2})\\&= -\dfrac{|V_{0}|}{\omega L}\cos\omega t}$
となります.
コイル1の電流が変化することで,コイル2を貫く磁束が変化し,誘導起電力が生じる.
これを相互誘導という.$\varDelta t$の間にコイル1の電流の変化が$\varDelta i$であるとき,コイル2の総誘導起電力の大きさ$V$は,相互インダクタンスを$M$として
$\eqalign{V&=|\lim_{\varDelta t\rightarrow 0}\dfrac{\varDelta \varPhi}{\varDelta t}|\\&=\dfrac{d\varPhi}{dt}}$
★ ファラデーの電磁誘導の法則
$\eqalign{V_{2}&=\dfrac{d\varPhi}{dt}\\&=\dfrac{d}{dt}(-\dfrac{|V_{0}|}{\omega L}\cos\omega t)\\&=-\dfrac{M|V_{0}|}{\omega L}(\omega )\sin\omega t\\&=\dfrac{M|V_{0}|}{L}\sin\omega t}$
したがって,コイル2を流れる電流$i_{2}$は,抵抗について,電流と電圧の位相が変化しないことに注意して,
$i_{2}=\dfrac{M|V_{0}|}{RL}\sin\omega t$
これより,コイル2の電流の振幅は$\dfrac{M|V_{0}|}{RL}$(答)

コメント